scaling이나 translation은 행렬으로 표현하지 않아도 직관적으로 이해하기 쉬운 transform들이다. 하지만, 개인적으로 rotation만큼은 행렬 연산을 통해 이해하는 것이 훨씬 효율적인 편이라 생각하고, 회전을 공부하면서 이해가 어려웠던 부분과 3차원 회전을 공부하면서 찾은 Rodrigues 공식에 대해 알아보았다.

2차원에서의 회전

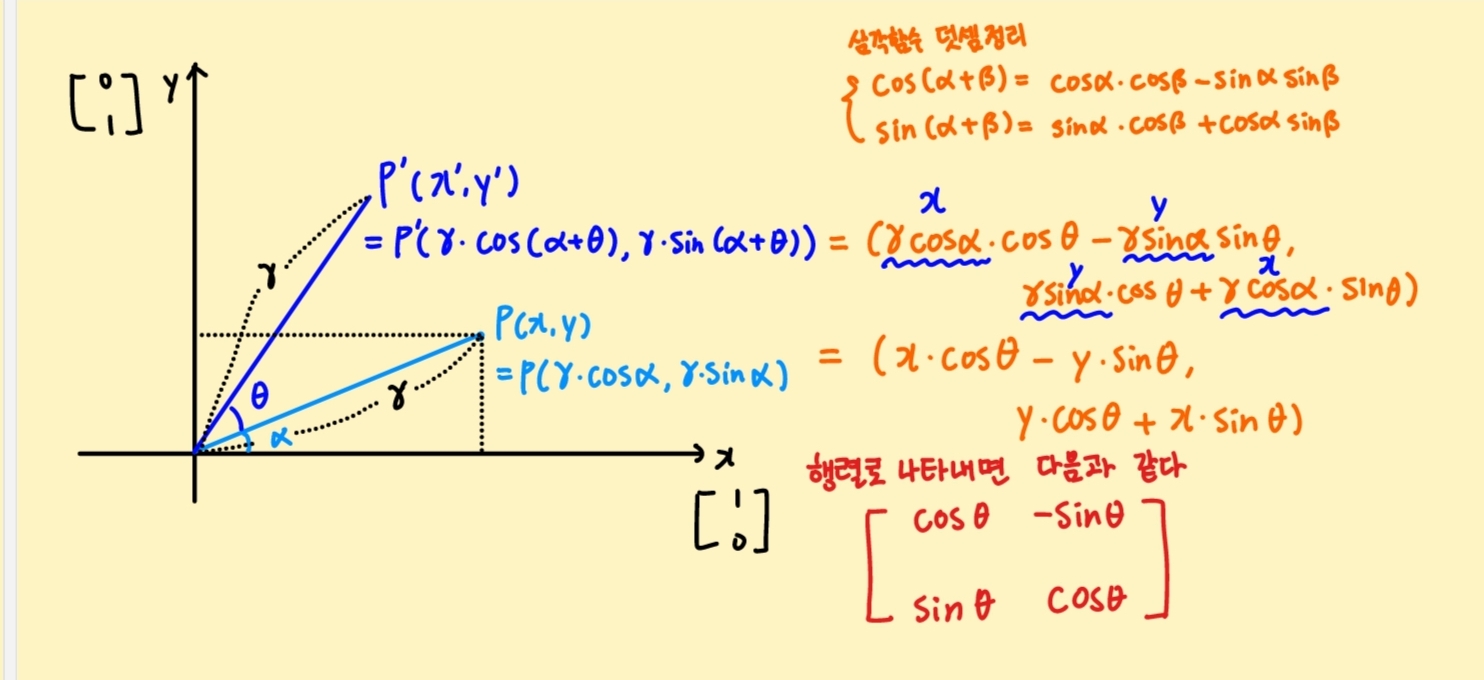
• 2차원에서의 회전은 원점을 기준으로 벡터를 회전시킨다. 회전은 벡터의 크기는 바꾸지 않기 때문에 이 성질과 삼각비를 사용해 간단하게 증명할 수 있다.

3차원에서의 회전

(1) 일반적인 축 회전의 이해

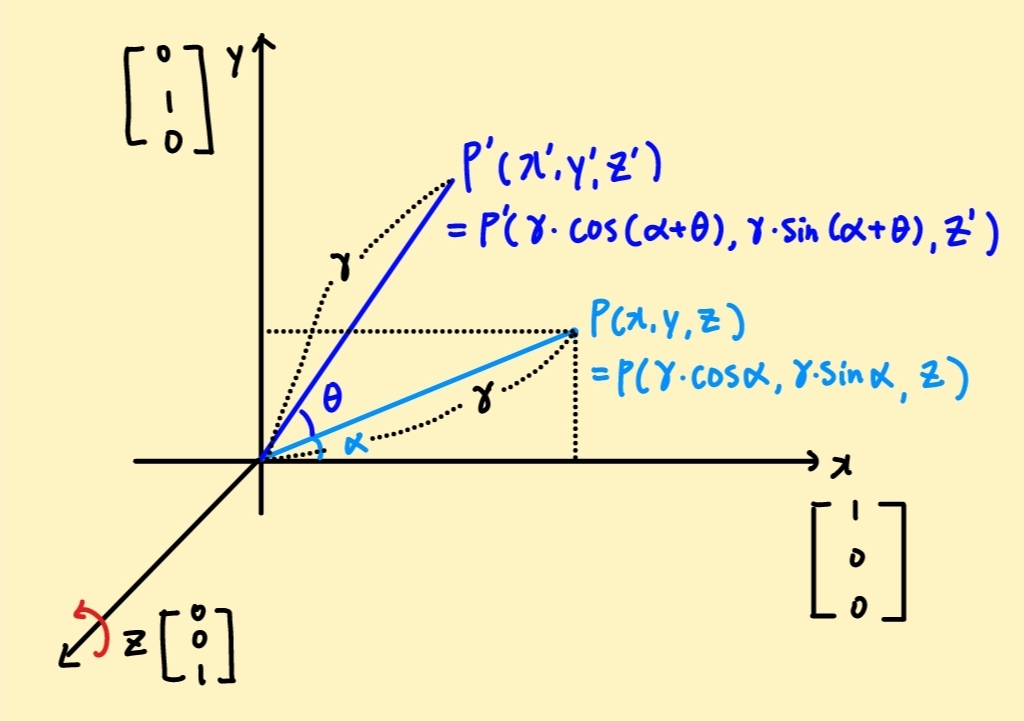
• 2차원에서는 원점을 기준으로 회전했다면, 3차원에서는 x,y,z축을 기반으로 회전한다. 각 축은 방향 벡터로 표현된다. 2차원 회전을 이해했다면, 그것을 바탕으로 축 회전 역시 이해하기 쉽다. 축에 해당되는 좌표값은 회전 이전, 이후에도 변하지 않기 때문이다.
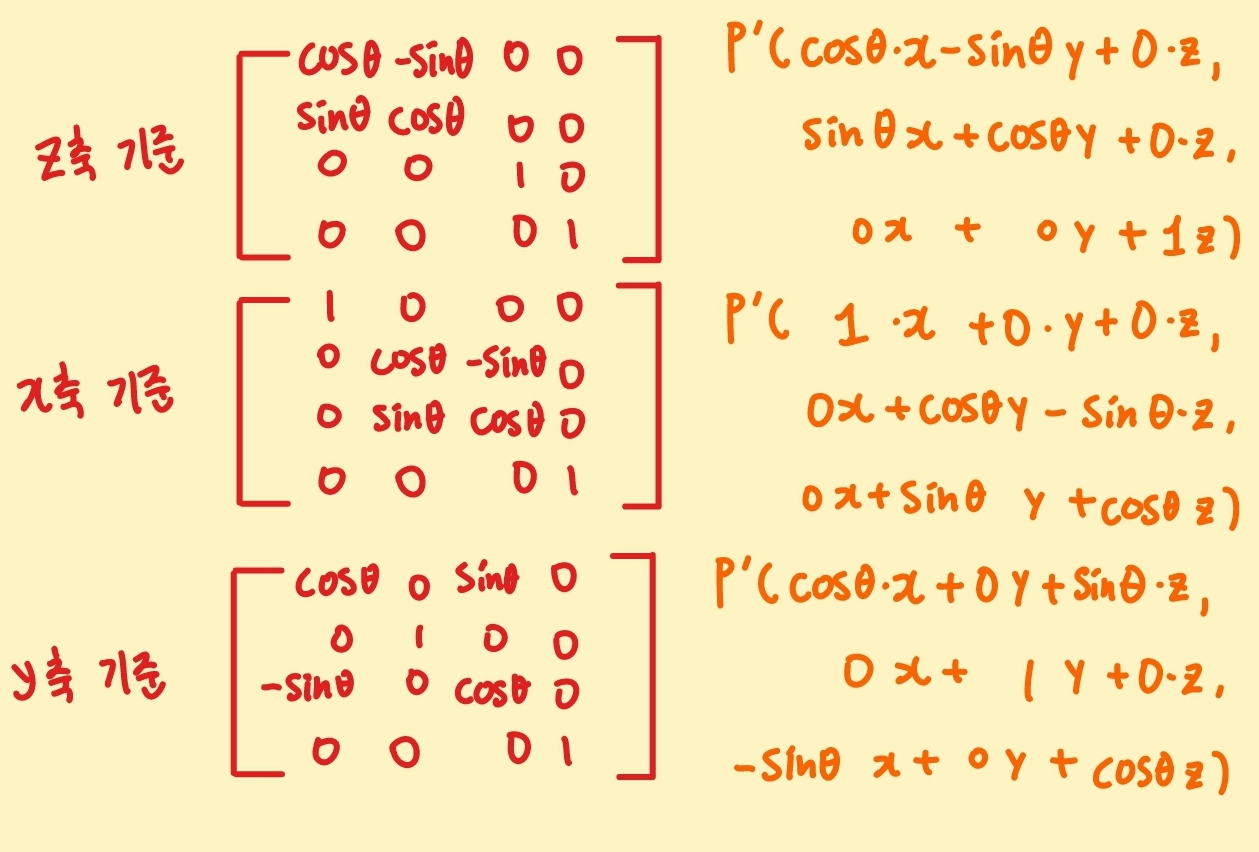
• 이를 바탕으로, x축, y축, z축 회전 행렬을 정리하면 다음과 같다. y축 회전이 다른 축 회전과 다른 배열을 가지는 이유는 회전되는 x축과 z축이 서로 대칭되지 않기 때문이고 이로 인해 sin값이 서로 반대 방향으로 scaling된다(하나가 +이면 다른 하나는 -이다).
  

Rogrigues' Rotation Formula

• Rogrigues' 회전 공식은 회전축, 회전각, 회전시킬 벡터가 주어졌을 때 회전된 벡터 값을 구하는 공식이다. 앞에서 보았던 축 별로 나눈 행렬과 달리, 이 공식은 하나의 식(행렬)으로 모든 회전을 설명할 수 있다. 아직 공식만 보고 증명할 수 있는 수준이 아니라, 공식이 설명된 위키피디아를 참고해 이해한 것을 정리해보려고 한다.
  https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula

• 공식은 위와 같다. 각 성분이 어떤 것을 의미하는 지를 차근차근 알아보자

• k벡터는 회전할 축, v벡터는 회전시킬 벡터이다. k벡터는 크기가 1인 단위 벡터이다. 각 세타만큼 회전시켜 v rot벡터를 구할 것이다.
  

• v rot 벡터는 v 직교 rot 벡터(수직 표시)와 v 평행 rot 벡터(평행 표시는 작대기 두 개!)의 합이다. v rot 벡터를 구성하는 두 가지의 벡터를 k와 v를 사용해 표현할 수 있다면, v rot 벡터를 나타낼 수 있다(공식 도출 가능!)

• v 평행 rot 벡터는 v 평행 벡터를 각 세타만큼 회전시킨 것이다. 회전하기 전과 회전한 이후, 벡터의 크기가 방향이 달라지지 않았기 때문에 v 평행 rot 벡터는 v 평행 벡터와 같다. 결국 v 평행 벡터를 구하면 된다!
• v 평행 벡터는 k와 v 벡터의 내적 값에 k벡터를 곱한 값이다. 내적 값은 k벡터가 단위벡터이기 때문에 v벡터의 길이와 cos값의 곱이다. 좀더 자세하게 보면, 내적 값은, v벡터가 k벡터 방향에 얼마나 가까운지 scalar값(v벡터의 길이 값)으로 표현한 것이다. 이에 k벡터를 구하면, v 평행 벡터를 구할 수 있다.

• 다음으로, v 직교 rot 벡터는 v 직교 벡터를 먼저 구해야 한다. v 직교 벡터는 v 벡터가 v 직교 벡터와 v 평행 벡터의 합이라는 것이 이용해, v - (k, v 내적 값 x k)으로 표현할 수 있다. 이는 vector triple product 정리를 사용해 다시 - k와 (k와 v의 외적값)의 곱으로 표현할 수 있다.(vector triple product도 나중에 기회가 되면 유도식을 정리해볼 것이다
  
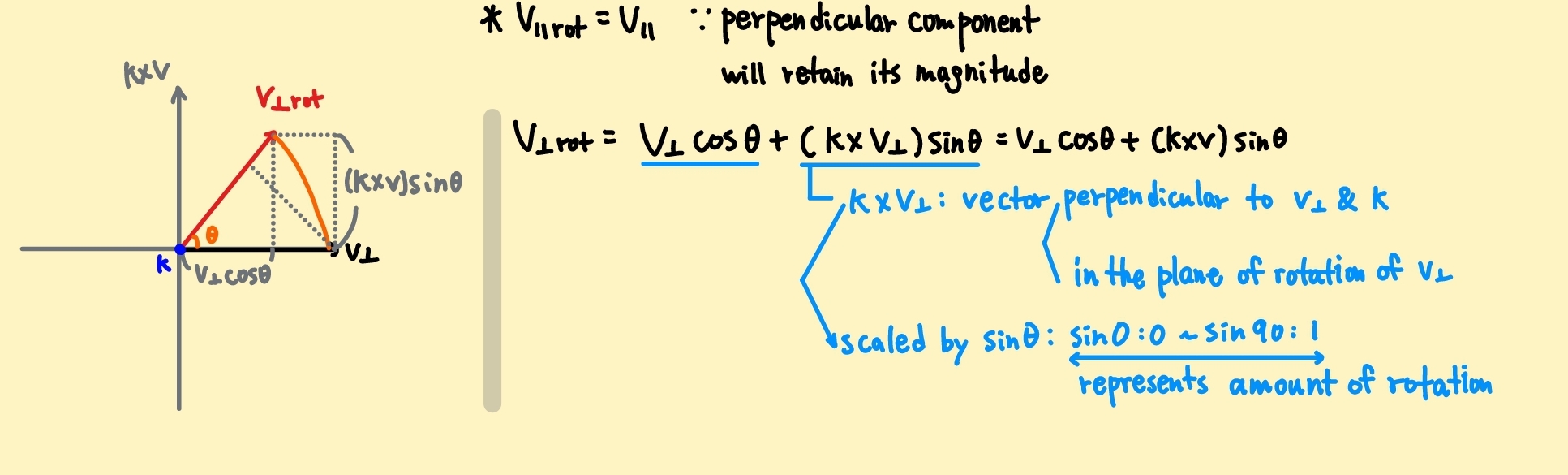
• 위의 그림은 k벡터를 기준으로 위에서 내려다 본 그림이다. v 직교 rot 벡터는 위의 그림에서 보이는 직각 삼각형의 빗변에 해당한다. 나머지 두 변의 벡터를 구하면, v 직교 rot 벡터도 구할 수 있다.
• 먼저, v 직교 벡터에 종속되어 있는 삼각형의 아랫변은 삼각형의 닮음을 사용해 구하면 v 직교 벡터에 cos값을 곱한 것이다.
• 그리고, 나머지 변은 k와 v(또는 v 직교 벡터)의 외적 값과 sin값의 곱이다. 외적 벡터는 k, v 벡터와 수직이면서 v 직교 벡터가 회전하는 면에 종속되어 있다. 외적 벡터에 v 직교 rot 벡터가 회전하는 정도를 표현(scaling)하는 sin값을 곱해서 구할 수 있다.
  
• 마지막으로, 지금까지 구한 값을 정리하면 Rogrigues' 회전 공식을 도출할 수 있다.
• 그리고, 이 공식을 외적 행렬(cross-product)로 변환하면 우리가 그래픽 라이브러리에서 사용하는 행렬을 도출해낼 수 있다.
  

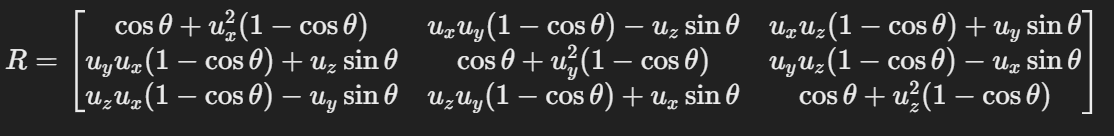
Summary

• 이 공식의 유도식을 정리하겠다고 마음 먹게 된 계기는 사소했다. OpenGL API로 모델 뷰어에 들어갈 커스텀 수학 라이브러리를 짜고 있는데, 회전 행렬을 연산하는 함수의 레퍼런스를 찾아보다가 이 공식을 발견했다. 제대로 알지 못하는 것을 사용하는 것 만큼 초심자에게 해로운 것이 없을 것이라는 믿음에 따라 1주일(......ㅠ)동안 ChatGPT와 위키피디아, linear Algebra 책을 읽어가면서 정리했다. 다른 분들도 이 공식에 대한 모호함이 조금이나마 해소되었으면 한다.
  https://github.com/GatsLee/Simple3DModelViewer