[SRCNN]

[Abstract]

• 이 논문은 Deep Learning을 이용하여 single image SR에 대해 설명하고 있다.
• direct로 low/high resolution image사이의 mapping 방법을 end-to-end로 학습시킨다.
• Mapping은 CNN을 이용하여 low-resolution의 input을 high-resolution의 output으로 만들어낸다.
• 모든 layer에 optimmize를 했다.
• deep CNN은 비록 가벼운 모델이지만, state-of-the-art의 quality를 보여준다.

[Introduction]

• Single Image Super Resolution은 "저해상도 영상을 고해상도 영상으로 복원하는 것"이다.
• 하나의 input으로부터 여러 result가 나올 수 있기 때문에 "ill-posed problem"이라고 한다.
• SRCNN은 low-resolution images로부터 High-resolution images로 직접 end-to-end mapping하는 방법을 학습하는 convolutional neural network를 제안한다.

[특징]

1. 구조는 매우 간단하지만, 다른 example-based SOTA 방법(Bicubic, sparse-coding based method)과 비교했을 때 뛰어난 성능을 보인다.
2. 적절한 filter와 layer를 사용하여 CPU에서도 온라인에 사용할 수 있을 만큼 빠르다.
3. 더 크거나 다양한 dataset이나 더 깊은 model을 사용시 성능이 향상될 것이다.

[Contribution]

1. Image super-resolution을 위한 fully convolutional neural net 제시했다.
2. Deep learning based SR과 Sparse-coding based SR 사이의 관계 설정했다.
3. DL이 super resolution이라는 컴퓨터 비젼문제에 유용하다는 것을 보여준다.

[추가한 것]

1. larger filter size in the non-linear mapping layer를 사용해서 SRCNN의 성능을 높였다.
2. SRCNN을 확장하여(?) 3 color channel을 동시 처리한다. (RGB&YCbCr)
3. 초기 결과에 분석과 직관적인 설명을 추가했다.(?)

[Convolutional Neural Networks For Super-Resolution]

1. Formulation

   Low resolution input image에 대해서 bicubic interpolation을 적용하여 image Y를 만드는 것이다. (image Y= input) ⇒ 목표는 high resolution image X와 최대한 유사하게 image Y를 mapping하는 F를 찾는 것이다. (image X=GT)

   

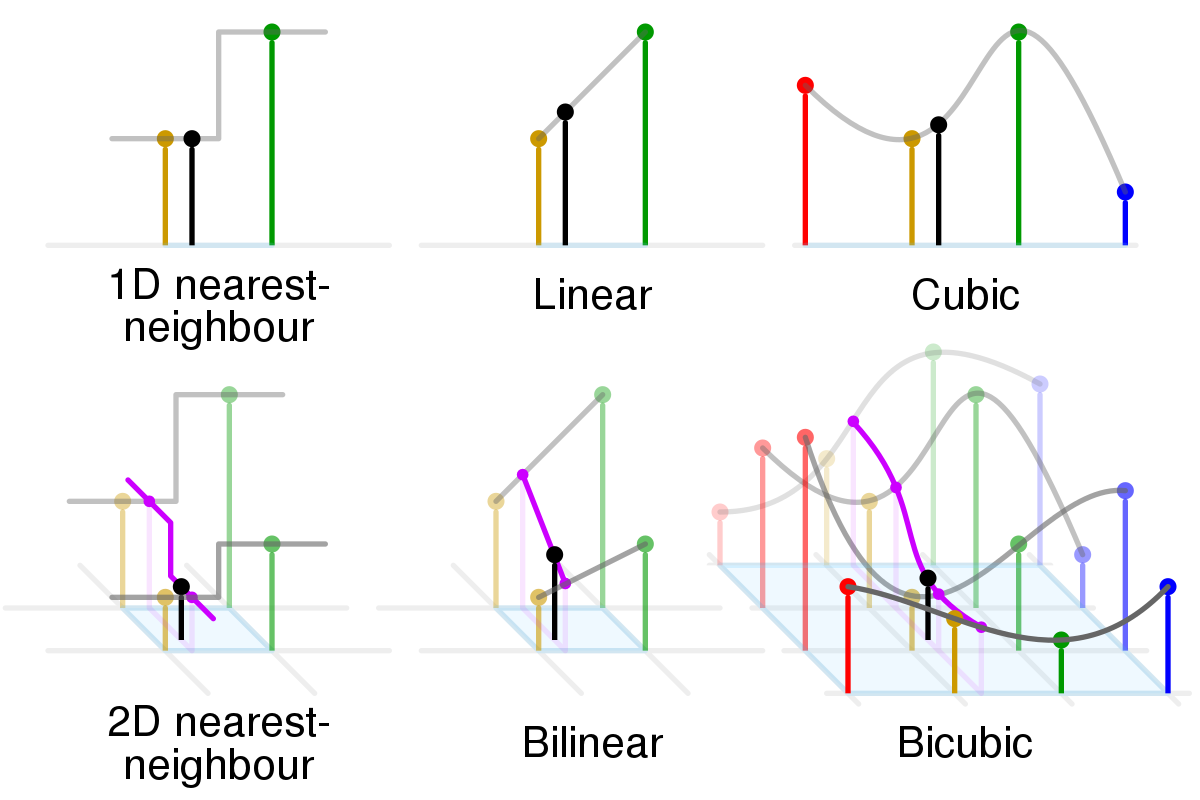
   Bicubic Interpolation이란?
   인접한 16개 화소의 화소값과 거리에 따른 가중치의 곱을 사용하여 결정하는 것.
   Cubic interpolation을 x축과 y축으로 각각 실행하여 구할 수 있음.
   ****다양한 interpolation option들이 존재하지만 해상도를 높이기 위해서는 보통 bicubic, bilinear, lanczos를 사용한다고 한다.

[Patch extraction and representation]

⇒ 즉, 저해상도 이미지에서 patch들을 추출하는 과정이다.

image Y로부터 patch를 추출하고, 각 patch에 대해서 CNN을 통과시켜 feature map을 생성한다.

각 patch는 high-dimensional vector로 representation한다. (이 vector들은 feature map)

첫 번째 layer는 F1으로 표현되고, 이후 ReLU를 적용한다.

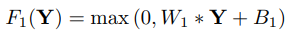
W1: filters (size: c×f1×f1×n1), B1: biases

c: the number of channels in the input image

f1 the spatial size of a filter

n: the number of filters

[Non-linear mapping]

⇒ 즉, 한 vector에서 다른 vector로 nonlinearly mapping한다. 각 mapped vector는 high-resolution patch를 나타낸다.

첫 번째 layer는 n1차원의 feature를 뽑고, Non-linear mapping에서는 n1 차원 벡터들을 n2 차원 벡터로 mapping 한다.

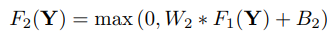
Non-linearity를 높이고 싶으면 conv layer를 더 쌓으면 된다.⇒ But complexity가 높아지게 되고, 결국 학습시간이 늘어나게 된다.

[Reconstruction]

앞에서 만든 patch들을 모아서 high-resolution image를 만든다.

이때 나온 image는 GT인 X와 비슷하게 나올 것이다.

기존의 방법들은 최종 이미지를 만들기 위해 patch의 평균을 구했는데, 이건 vector들을 flatten하게 만들기 때문에 다른 layer를 설계했다.

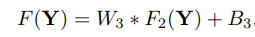
2. Relationship to Sparse-Coding-Based Methods

   

   Sparse-coding-based 방식과 다르게, SRCNN에서 non linear operation(patch extraction과 representation) 과정이 학습 과정 내에서 최적화가 이뤄진다. (?

   따라서 low resolution dictionary, high resolution dictionary, non-linear mapping 등이 모두 최적화 대상에 포함된다. `

   External example based 방식에 비해서 reconstruction을 위해 더 많은 정보가 사용되고, 이로 인해서 SRCNN이 더 좋은 성능을 낼 수 있다.

3. Training

   loss function : MSE

   metric : PSNR (MSE가 작아질수록 PSNR은 커져서 화질 개선을 더 잘할 수 있다.)

   Optimizer : SGD

   learning rate: 0.0001(1,2번째 layer) & 0.00001(3번째 layer)

   

   Bicubic, SC, SRCNN의 psnr 비교표를 봐도 월등히 좋은 성능을 내는 것을 볼 수 있다.

   Dataset: 91개의 images로 되어있는 작은 Dataset과 약 39만개로 되어있는 ImageNet detection training set을 사용하여 비교해보았다.

   

   image의 양이 많을수록 학습이 잘되는 것을 확인할 수 있다.

   

   filter의 수가 증가하면 PSNR이 증가하여 화질 개선이 잘 이뤄지지만, training time이 길어지는 것을 볼 수 있다.

   

   filter size가 커질수록 성능이 좋아지는 것을 확인할 수 있다.

   

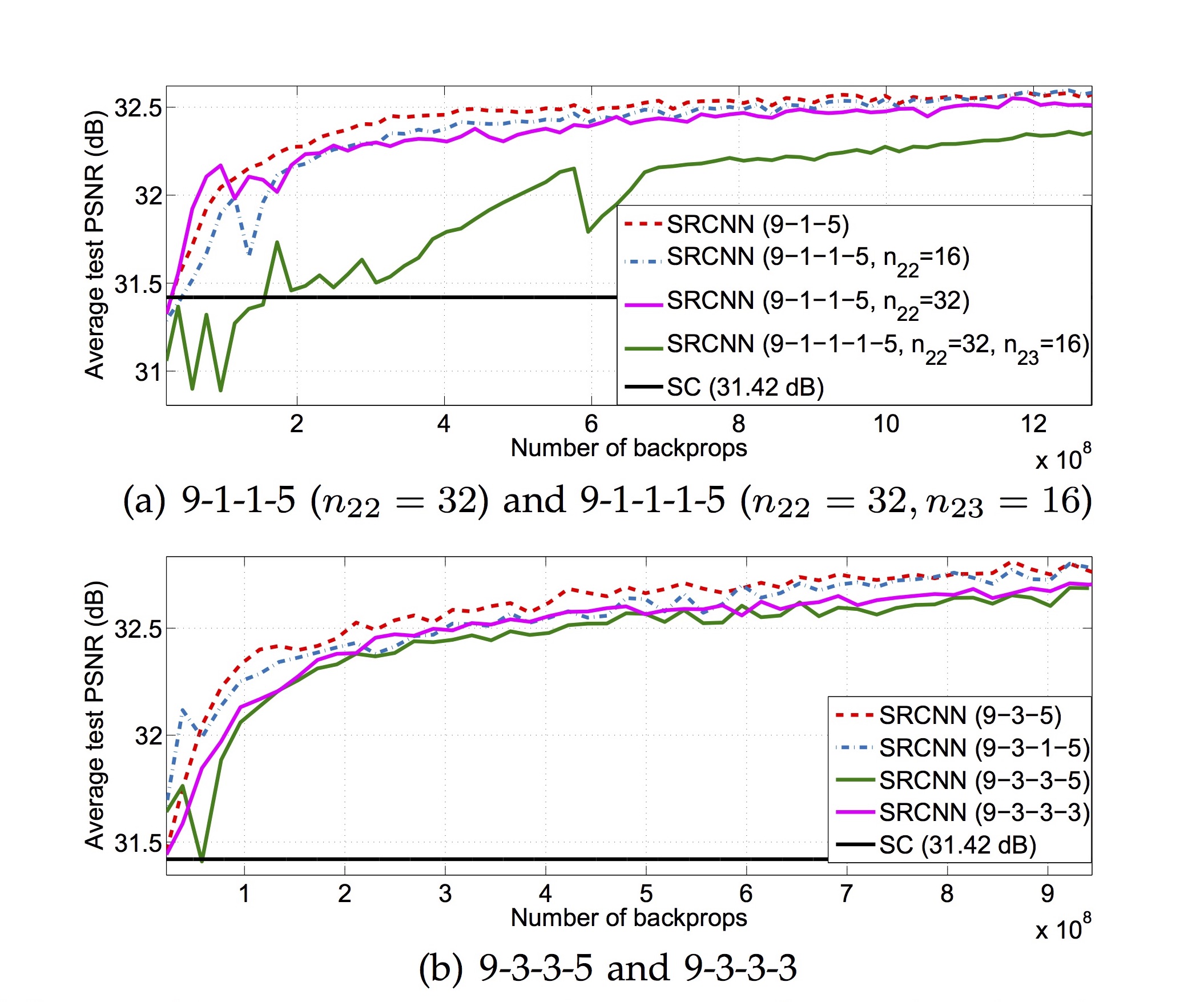
   layer의 깊이는 깊을수록 성능이 떨어진다.

   ⇒ 이 논문에서는 YCbCr에서 Y에만 적용시켰지만, 이후 연구에서 RGB 채널에 적용시켰을 때 더 좋은 결과를 나타냈다고 한다.

   

[FSRCNN]

[Abstract&Introduction]

SRCNN의 문제점

⇒ 이전의 다른 learning-based 방법들과 비교했을 때는 빠르지만 큰 이미지에서 속도가 느리다.

3가지의 방법을 도입했다.

1. bicubic interpolation 대신 deconvolution(transposed convolution)을 네트워크 후반에 활용하여, 저해상도의 입력 이미지와 고해상도의 출력 이미지간의 mapping이 End to End 로 학습 가능한 네트워크 구조를 만든다.
2. transposed convolution을 통해 feature map을 확장시키기 전에 input feature map의 차원을 축소시켜 latent feature를 추출할 수 있도록 한다.
3. 더 작은 필터 크기를 사용하여 연산량을 줄이고, 대신 더 많은 layer를 사용한다.

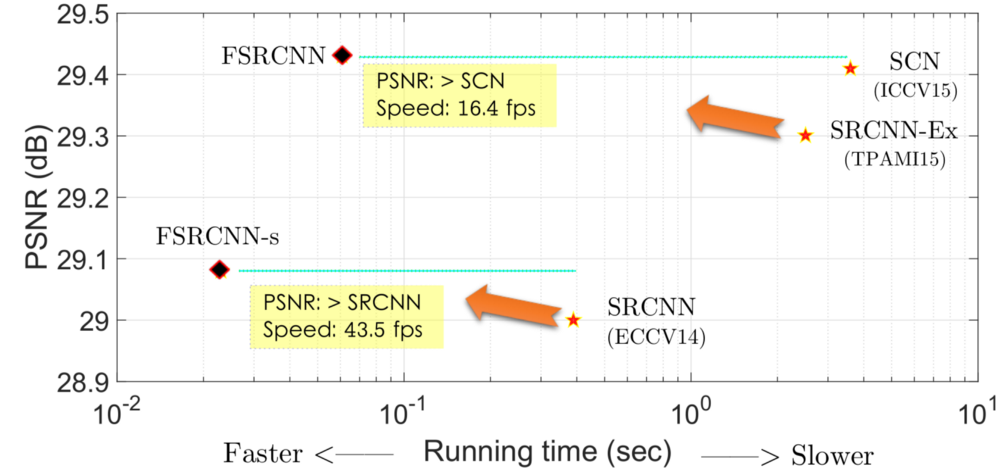
SRCNN은 real-time으로 결과를 내기에는 너무 느리다.

SRCNN의 속도 한계의 원인은 2가지다.

1. 전처리 단계에서 입력 LR 이미지는 bicubic interpolation을 통해 원하는 image size로 upsampling 되는데 이때 upsampling된 image에 대해서 convolution을 수행하면 계산 비용이 크게 증가한다. ⇒ transposed convolution을 사용한다. (original image에 대해서 convolution을 수행하기 때문에 n^2만큼 연산량을 줄일 수 있다.)

   ex) n배의 크기로 upsampling하는 경우, original image 대비 n^2배만큼 연산량이 증가한다.

2. SRCNN에서 다차원 LR feature space에서 또 다른 다차원 HR feature space로 mapping하는 non-linear mapping 단계에서 convolution layer의 너비를 늘릴 수록 좋은 accuracy를 얻을 수 있지만, 연산량이 증가한다. ⇒ pix2pix에서 그러듯 대칭적인 encoder-decoder구조를 사용한다. (called 모래시계구조)

FSRCNN의 장점

encoder 부분에 있는 모든 convolution의 layer가 decoder의 upscaling factor가 달라져도 동일하게 재사용이 가능하다 ⇒ 다양한 upsampling factor에 대해서 Train, Test가 용이하다.

따라서, 학습 과정에서 encoder의 convolution layer는 pretraining된 것을 그대로 사용하고, decoder의 transposed convolution만 upsampling factor에 맞게 fine-tuning하면 된다.

[FSRCNN]

총 5단계의 Network 구조를 가진다.

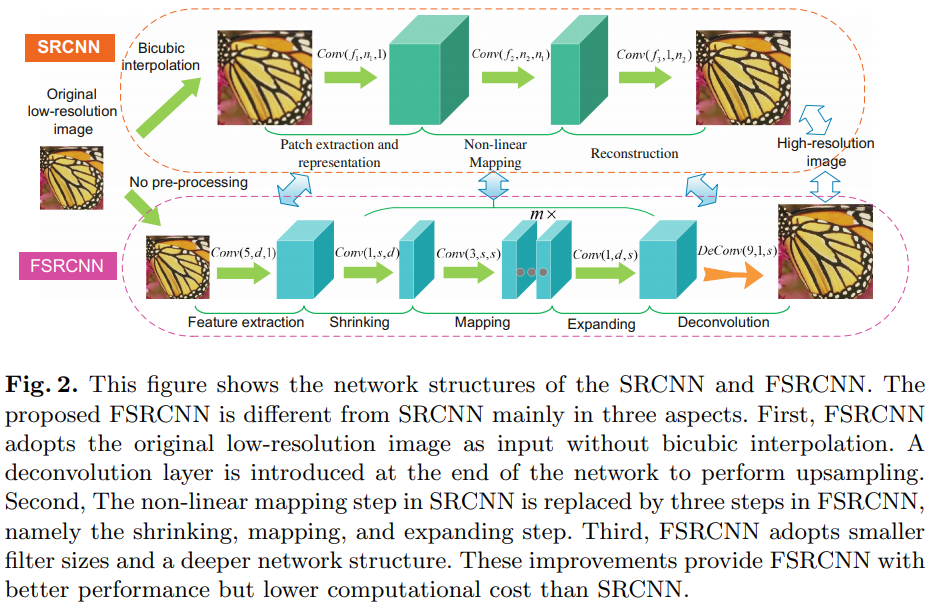
앞의 4개의 구조는 convolution layer이고, 뒤에 하나가 transposed layer이다.

1. Feature extraction

   SRCNN의 첫 번째 단계와 동일한 연산, But 입력 이미지가 bicubic interpolation을 거친 이미지가 아니라 original image이다.

   SRCNN에서는 첫 번째 레이어에서 9X9 filter를 사용하는데, 이는 interpolation을 통해 upscaling된 image라 그런거고, FSRCNN에 대해서는 5X5 filter를 적용한다.

2. Shrinking

   SRCNN에서 non-linear mapping 단계에서 LR feature space에서 HR feature space로의 mapping이 바로 이루어졌지만, 이러면 LR feature vector의 채널 수가 일반적으로 상당히 큰 값이어서 이대로 convolution 수행하면 연산 비용이 너무 커진다.

   ⇒ 1X1 convolution을 통해 채널 수를 줄여준다.(=오버헤드 감소)

3. Non-linear mapping

   이때 가장 중요한 요소가 filter 개수와 layer 개수다.

   SRCNN에서는 5X5 layer를 사용했을 때가 1X1 layer를 사용했을 때보다 좋은 성능이었지만 이건 layer 깊이가 얕을 때에 대해서만 실험한 것이다.

   FSRCNN은 1과 5 중간인 3을 filter크기로 잡고, 줄어든 연산량만큼 layer의 깊이를 늘렸다. 이 때 feature map 채널 수의 일관성을 위하여 filter 개수는 입력 채널수와 같게 잡는다.

4. Expanding

   Shrinking 단계에서는 1x1 conv을 통해서 채널 수를 줄여 연산량을 감소시켰으면,

   Expanding 단계에서는 SR 성능을 위해서 feature map 채널 수를 shrinking 이전으로 복원한다.

   ⇒ 이 때도, 연산량이 적은 1x1 convolution을 활용한다.

5. Transposed Convolution

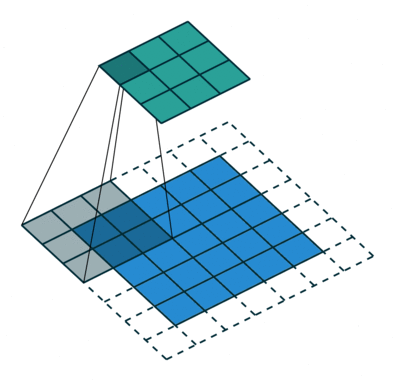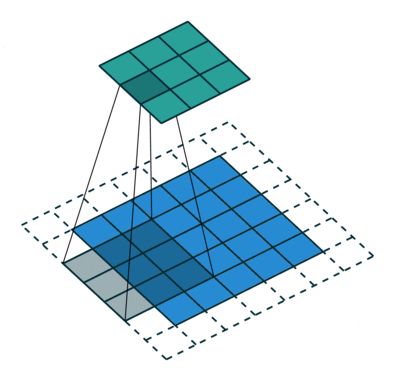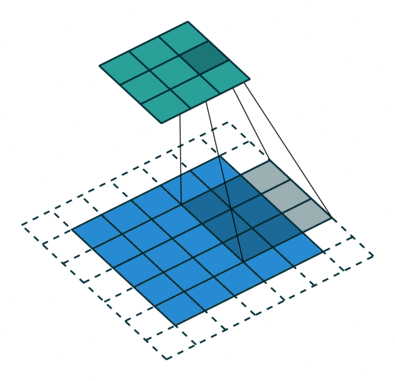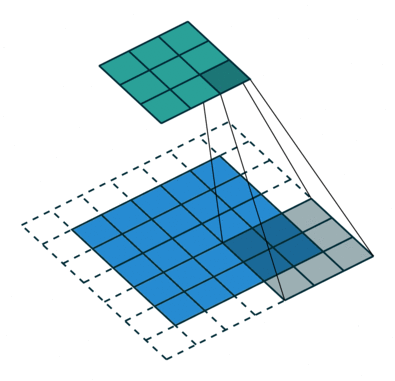
convolution

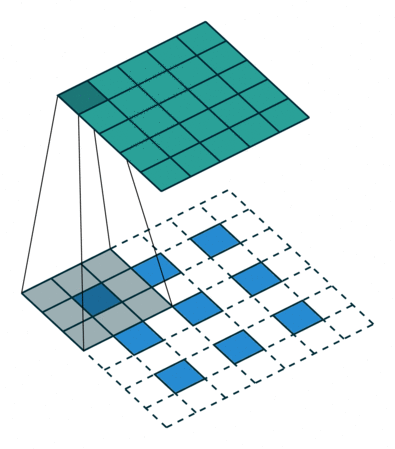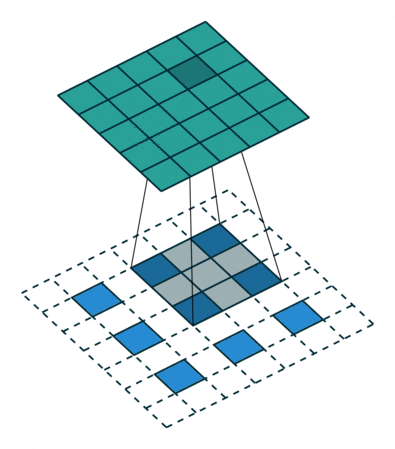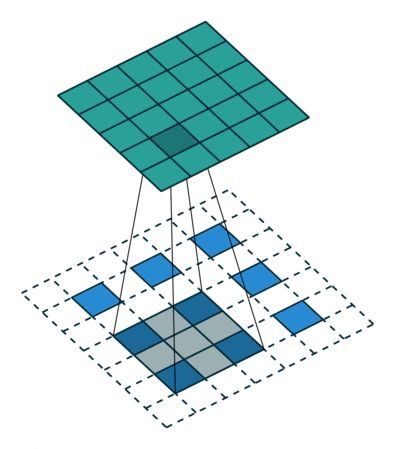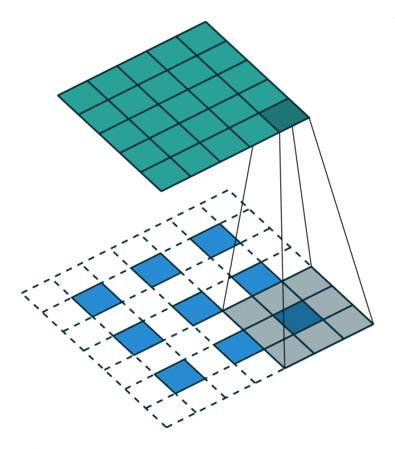
Transposed convolution (초록색이 출력, 파란색이 입력) stride=2, padding=1

Transposed conv는 conv를 통해 feature map을 다시 확장시키는 upsampling 기능을 한다.

Transposed conv에서는 출력 feature map의 크기가 stride 크기의 배수로 증가하기 때문에, stride가 곧 upsampling factor.

Transposed conv는 HR 이미지에서 feature를 추출하므로 9X9 filter를 사용했다. 이는 interpolation kernel들과는 달리 deconvolution layer는 upsampling kernel을 학습한다.

6. PReLU

ReLU를 사용할 때 zero gradient들로부터 만들어지는 dead feature를 없애기 위해 사용했다.

7. Overall Structure

Conv(5,d,1)−PReLU−Conv(1,s,d)−PReLU−m×Conv(3,s,s)−PReLU− Conv(1,d,s) −PReLU−Deconv(9,1,d)

8. Cost Funtion

   MSE 사용함.

[Differences against SRCNN : From SRCNN to FSRCNN]

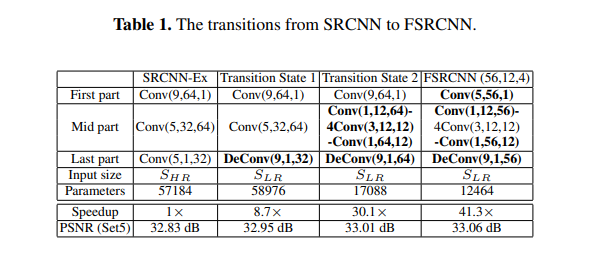
1. SRCNN-Ex: 57184 매개 변수를 사용하는 더 나은 버전의 SRCNN.
2. Transition state 1: Deconv를 사용하며, 58976개의 파라미터로 더 큰 PSNR를 가짐.
3. Transition state 2: 중간에 더 많은 convs이 사용되며, 17088개의 파라미터로 더 큰 PSNR을 가짐.
4. FSRCN(56, 12, 4): 필터 크기가 작고 필터 개수가 적으며, 12464개의 파라미터로 PSNR이 더 크다. 이러한 개선은 교육해야 할 매개변수가 적고 수렴이 용이하기 때문이다.

[Experiments]

Training dataset : 91-image dataset, new General-100 dataset that contains 100 bmp-format images(for fine-tuning)

Learning Rate : convolution⇒0.001, deconvolution⇒0.0001

Optimizer : SGD

d=LR feature dimension, s=the number of shrinking filters, m=mapping depth

[Result]

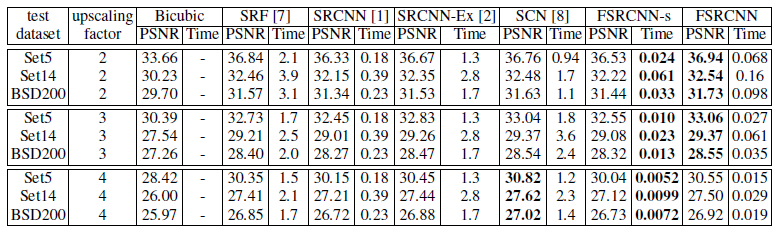
All-train

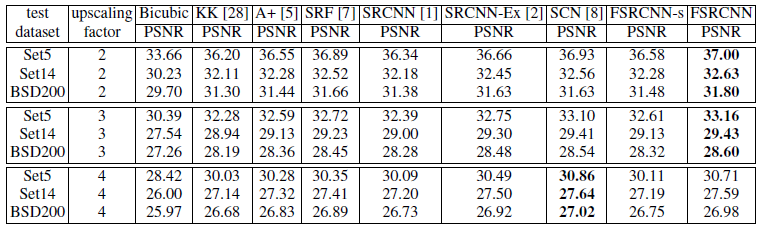
91 image train+100 dataset

upscaling factor 3으로 91 image dataset를 사용하여 네트워크를 처음부터 훈련한 다음 upscaling factor 2와 4로 General 100 dataset 만 추가하여 Transposed conv를 fine-tune했다.

upscaling factor를 4로 주었을 때 FSRCNN이 SCN보다 PSNR면으로 봤을 때 성능이 떨어지는 것을 확인할 수 있다.

upscaling factor 3

upscaling factor 3