Dataset : https://www.kaggle.com/yufengsui/mobile-games-ab-testing
Kaggle의 Cookie Cats 게임 데이터셋을 활용해 A/B test를 연습해보겠습니다.
먼저 데이터를 불러와 중복행을 제거하고 전체적인 구조를 확인해보겠습니다.
ab <- read.csv("cookie_cats.csv")
ab <- unique(ab)
str(ab)
str(ab)
'data.frame': 90189 obs. of 5 variables:
$ userid : int 116 337 377 483 488 540 1066 1444 1574 1587 ...
$ version : chr "gate_30" "gate_30" "gate_40" "gate_40" ...
$ sum_gamerounds: int 3 38 165 1 179 187 0 2 108 153 ...
$ retention_1 : logi FALSE TRUE TRUE FALSE TRUE TRUE ...
$ retention_7 : logi FALSE FALSE FALSE FALSE TRUE TRUE ...
데이터의 구조를 확인해 본 결과 5개의 변수와 90189개의 행으로 구성되어 있는 것을 알 수 있습니다.
각 변수에 대해 간략하게 설명을 하자면,
userid : 게임 플레이어의 고유 아이디
version : 게임 플레이어가 gate_30(control group) 혹은 gate_40에 해당하는 지 여부
sum_gamerounds : 게임 플레이어가 게임을 설치한 후 2주 동안 플레이한 횟수
retention_1 : 게임 플레이어가 게임을 설치한 후 하루 뒤에 다시 접속했는 지 여부
retention_7 : 게임 플레이어가 게임을 설치한 후 일주일 뒤에 다시 접속했는 지 여부
로 해석할 수 있습니다.
이제 데이터의 변수들을 각각의 타입에 맞게 변형한 뒤 간단한 EDA를 진행해보겠습니다.
ab$version <- factor(ab$version)
ab$retention_1 <- factor(ab$retention_1)
ab$retention_7 <- factor(ab$retention_7)ab %>% group_by(version) %>% count() %>% ggplot(aes(x=version, y=n, fill = version)) + geom_bar(stat = "identity") + geom_text(aes(label = n), size = 10)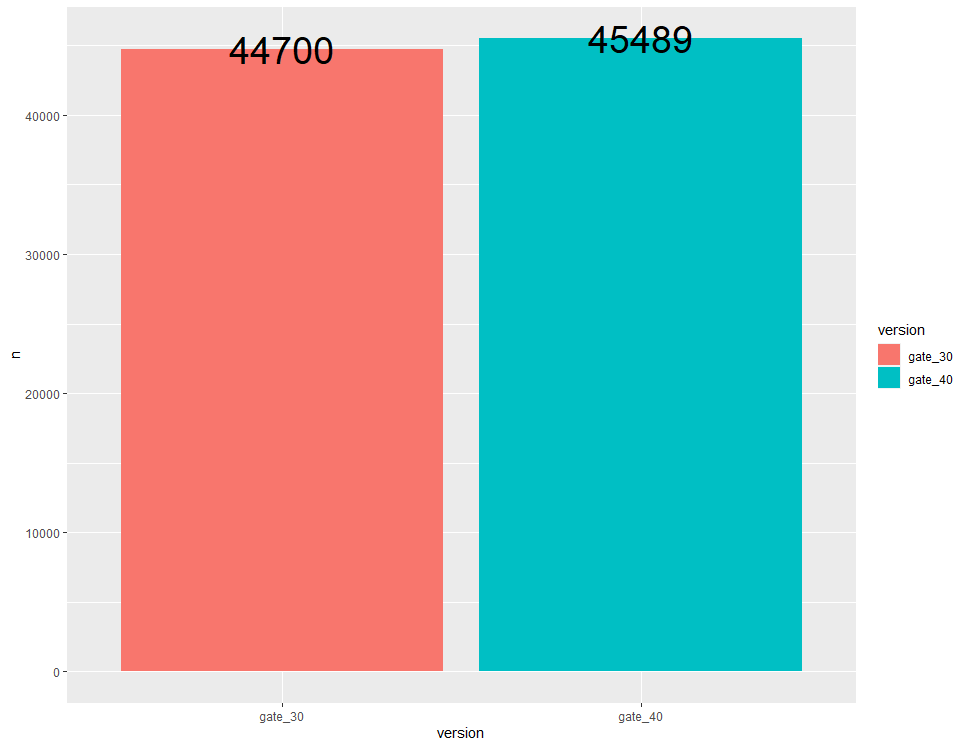
gate_40 그룹에 속하는 게임 플레이어 수가 gate_30 그룹에 속하는 게임 플레이어 수보다 아주 약간 많은 것을 확인할 수 있습니다.
ab %>% ggplot(aes(x=sum_gamerounds)) + geom_histogram()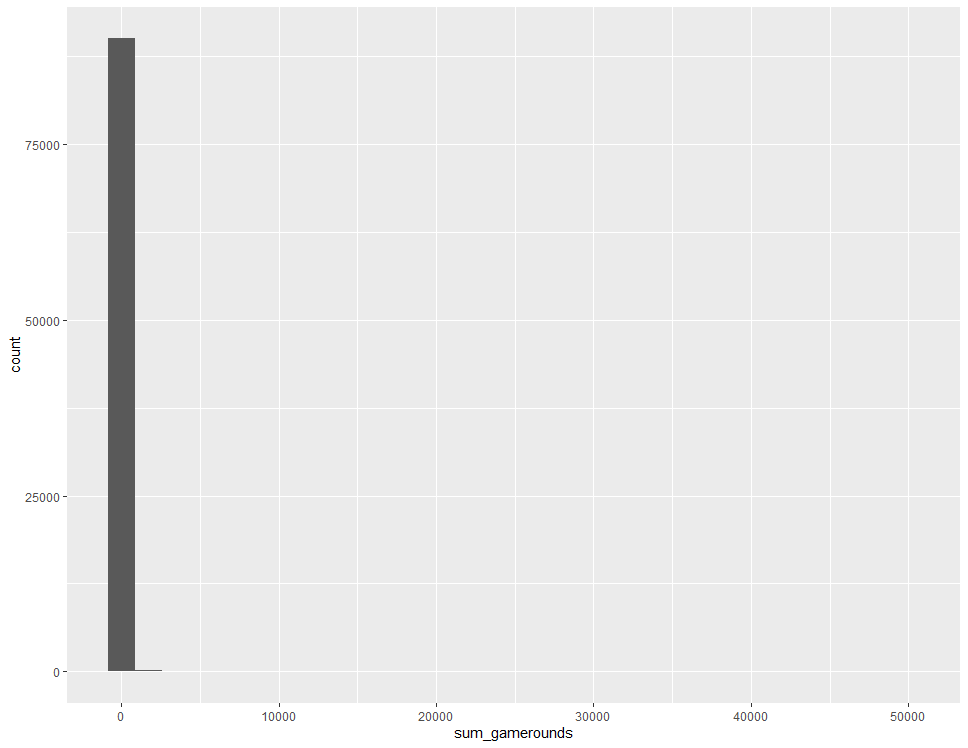
게임을 설치한 후 2주 동안 게임을 플레이 한 횟수에 대한 히스토그램을 보니 왼쪽으로 매우 치우친 형태를 보이고 있습니다.
아마도 게임의 경우, 게임을 플레이한 횟수가 플레이어에 따라 매우 많은 차이를 보이기 때문에 이러한 분포를 보이는 것으로 유추됩니다.
데이터가 정규분포가 아닌 경우에는 로그화 및 이상값 처리 등을 통해 해당 데이터를 정규분포화 해주는 것이 바람직하지만, 이번 연습에서는 생략하도록 하겠습니다.
ab %>% group_by(retention_1) %>% count() %>% ggplot(aes(x=retention_1, y=n, fill=retention_1)) + geom_bar(stat = "identity") + geom_text(aes(label = n), size = 10)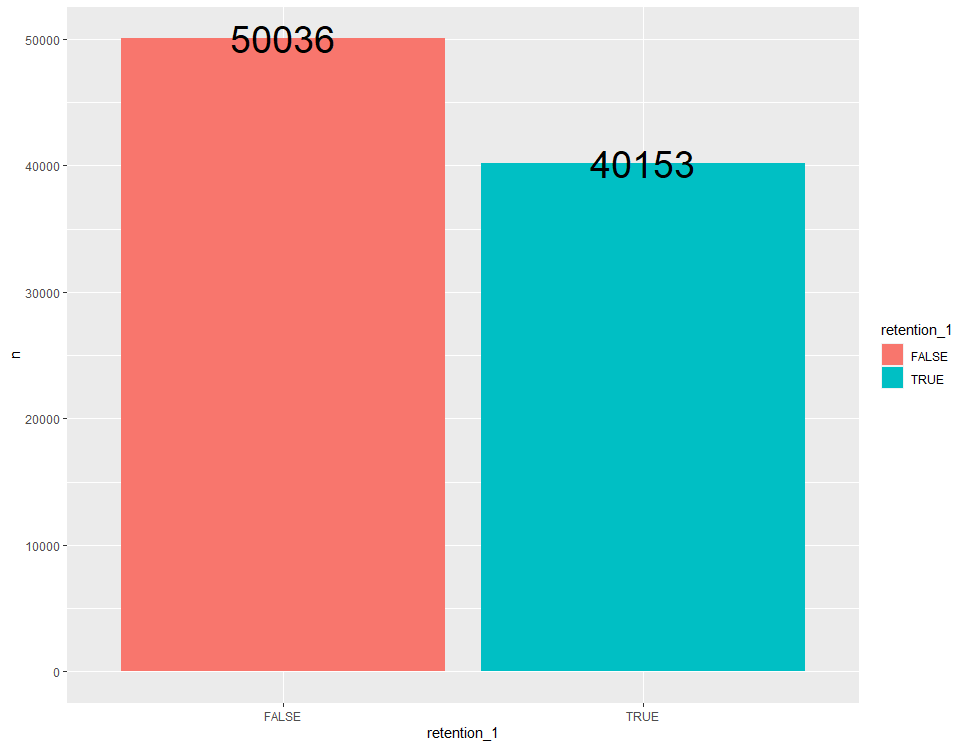
게임을 설치한 후 하루 뒤에 다시 접속했는 지 여부를 확인해보니 다시 접속한 플레이어 수가 다시 접속하지 않은 플레이어 수보다 적은 것을 알 수 있습니다만, 그 차이가 엄청나게 벌어지지는 않아 보입니다.
ab %>% group_by(retention_7) %>% count() %>% ggplot(aes(x=retention_7, y=n, fill=retention_7)) + geom_bar(stat = "identity") + geom_text(aes(label = n), size = 10)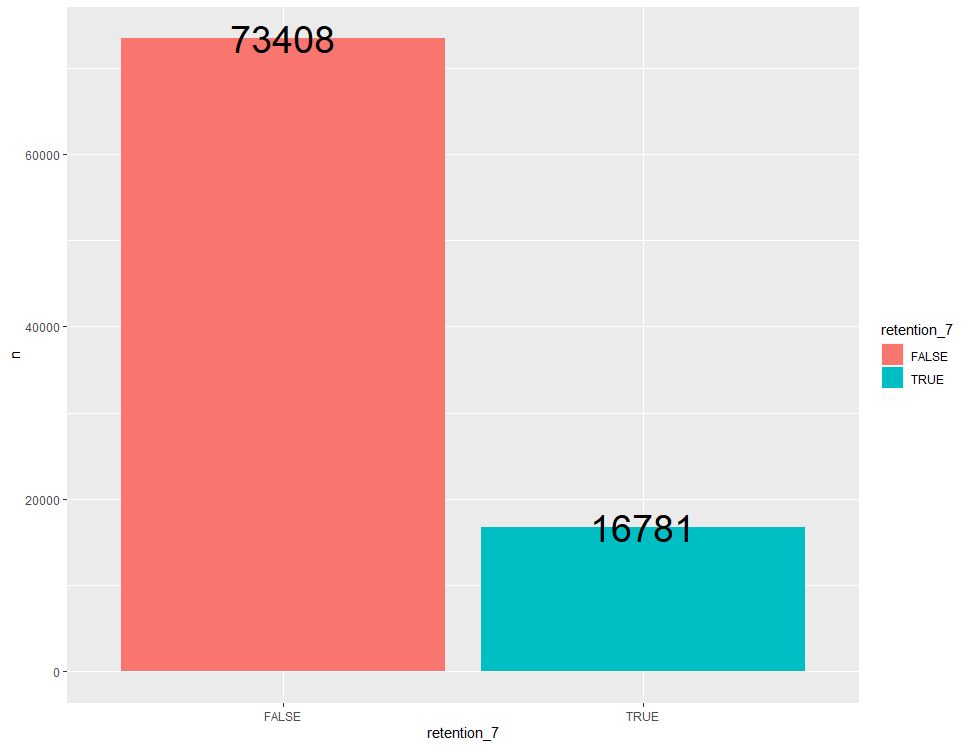
게임을 설치한 후 일주일 뒤에 다시 접속했는 지 여부를 확인해보니 다시 접속한 플레이어 수가 다시 접속하지 않은 플레이어 수보다 압도적으로 적은 것을 알 수 있습니다.
다만 하루 뒤에 다시 접속하는 것보다 일주일 뒤에 다시 접속한다는 것은 해당 게임에 대한 지속적인 관심과 선호가 있는 플레이어들에게만 해당되는 일이기 때문에 자연스럽게 시간이 지날 수록 다시 게임에 접속하는 플레이어 수는 줄어들기 마련입니다.
이렇게 간단한 EDA를 마쳐본 결과, 총 3가지 관점에서 A/B test를 적용해 볼 수 있을 것 같습니다.
gate_30은 구버전, gate_40은 약간의 수정을 가한 신버전이라고 해석할 수 있으니, 저희는 gate_30보다 gate_40에서 여러 지표가 향상되었는 가에 대해 관심을 가지게 됩니다.
-
gate_30에 해당하는 플레이어보다 gate_40에 해당하는 플레이어의 2주 동안 평균 게임 플레이 횟수가 더 많을 것이다.
-
gate_30에 해당하는 플레이어보다 gate_40에 해당하는 플레이어의 하루 뒤 다시 접속하는 비율이 더 높을 것이다.
-
gate_30에 해당하는 플레이어보다 gate_40에 해당하는 플레이어의 일주일 뒤 다시 접속하는 비율이 더 높을 것이다.
이렇게 총 3가지의 A/B 실험을 진행해보겠습니다.
1. gate_30에 해당하는 플레이어보다 gate_40에 해당하는 플레이어의 2주 동안 평균 게임 플레이 횟수가 더 많을 것이다.
plotmeans(sum_gamerounds ~ version, ab, mean.labels = T)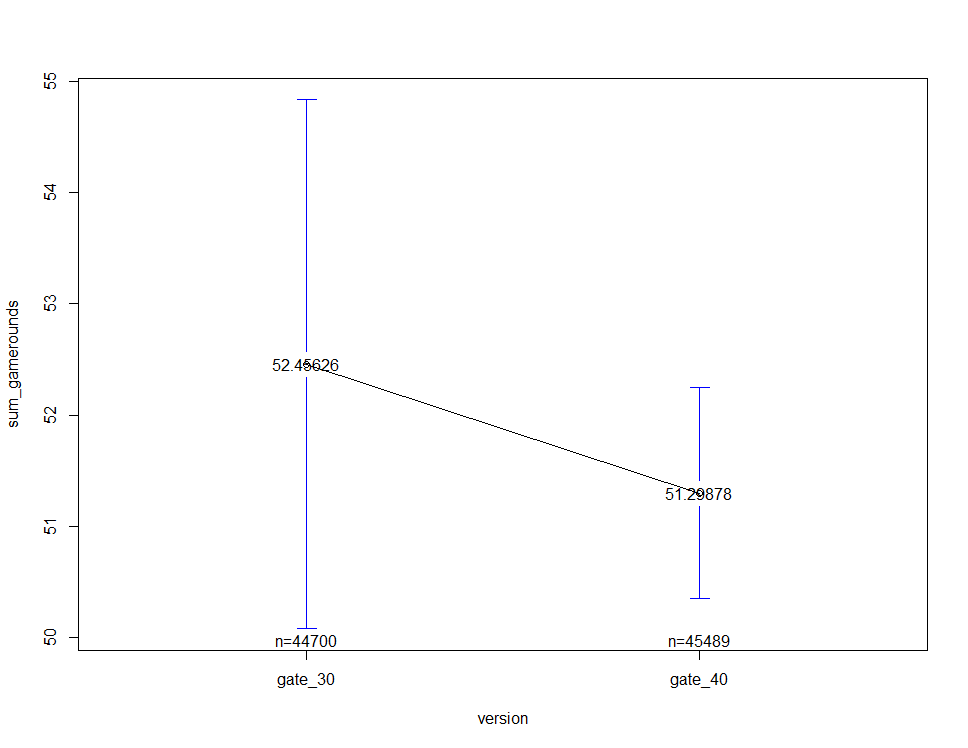
목표변수가 연속형 변수이니 독립표본 t 평균 검정을 사용하되, 먼저 각 그룹의 분산이 같은지 var.test() 함수를 통해 확인해보겠습니다.
(각 그룹의 속하는 데이터 수는 30개를 훌쩍 뛰어넘기 때문에 CLT에 의해 정규성 가정은 만족한다고 보겠습니다.)
var.test(sum_gamerounds ~ version, ab)F test to compare two variances
data: sum_gamerounds by version
F = 6.1767, num df = 44699, denom df = 45488, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
6.063685 6.291747
sample estimates:
ratio of variances
6.176659
등분산성 검정 결과 p-value가 0.05보다 작기 때문에 두 그룹의 분산은 동일하지 않다고 해석할 수 있습니다.
따라서 등분산성 가정을 만족하지 않는 독립표본 t 평균 검정을 수행하겠습니다.
t.test(sum_gamerounds ~ version, ab, var.equal = F, alter = "less")Welch Two Sample t-test
data: sum_gamerounds by version
t = 0.88544, df = 58595, p-value = 0.812
alternative hypothesis: true difference in means between group gate_30 and group gate_40 is less than 0
95 percent confidence interval:
-Inf 3.307758
sample estimates:
mean in group gate_30 mean in group gate_40
52.45626 51.29878
검정 결과 p-value가 0.812로써 0.05보다 매우 크게 나왔기 때문에 귀무가설을 채택하게 됩니다.
즉 gate_40에 해당하는 플레이어의 2주 동안 평균 게임 플레이 횟수는 gate_30에 비해 통계적으로 높다고 할 수가 없습니다.
2. gate_30에 해당하는 플레이어보다 gate_40에 해당하는 플레이어의 하루 뒤 다시 접속하는 비율이 더 높을 것이다.
ab %>% group_by(version, retention_1) %>% count() %>%
ggplot(aes(x=version, y=n, fill=retention_1)) + geom_bar(stat = "identity", position = "dodge") + geom_text(aes(label = n), size = 10)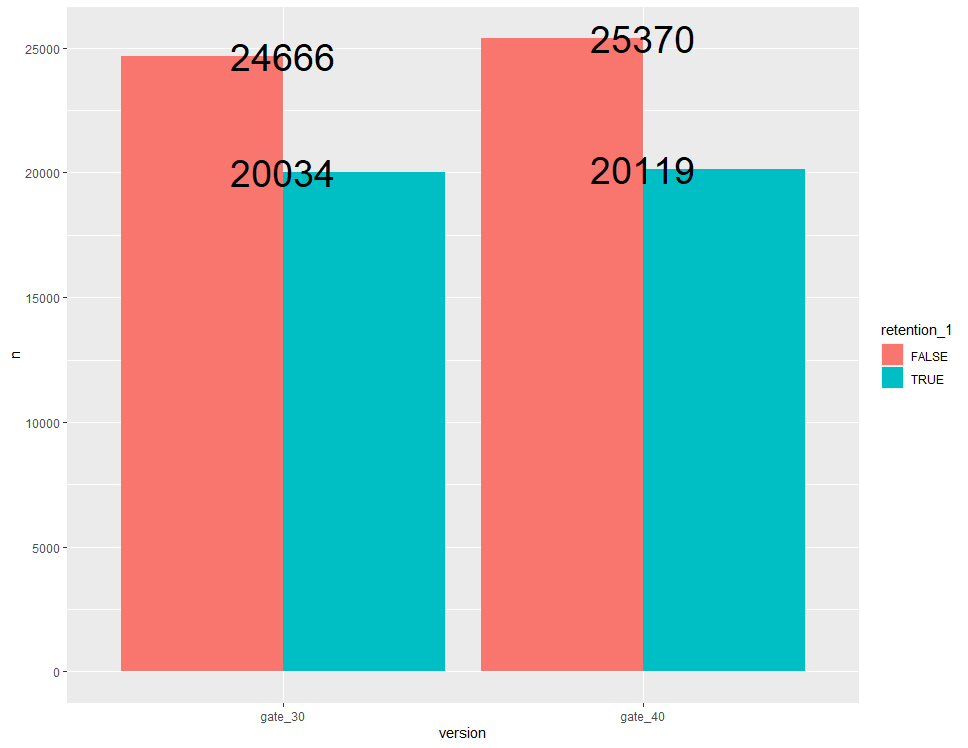
이번 가설검정에서는 목표변수가 False or True로 구성된 이항 범주형 변수입니다.
따라서 version과 retention_1 변수로 구성된 table 표를 만들어보겠습니다.
addmargins(table(ab$version, ab$retention_1), margin=2) FALSE TRUE Sum gate_30 24666 20034 44700
gate_40 25370 20119 45489
이 테이블 표에서 저희가 관심 있는 부분은 각 그룹에서의 TRUE(하루 뒤에 다시 접속한 플레이어의 수)의 비율입니다.
따라서 prop.test() 함수를 통해 두 그룹의 모비율 차이에 대한 검정을 수행하도록 하겠습니다.
prop.test(x=c(20034, 20119), n=c(44700, 45489), alter = "less")2-sample test for equality of proportions with continuity correction
data: c(20034, 20119) out of c(44700, 45489)
X-squared = 3.1591, df = 1, p-value = 0.9622
alternative hypothesis: less
95 percent confidence interval:
-1.00000000 0.01137164
sample estimates:
prop 1 prop 2
0.4481879 0.4422827
검정 결과 p-value가 0.9622로 0.05보다 매우 크기 때무에 귀무가설을 채택하게 됩니다.
즉 gate_40에 해당하는 플레이어가 하루 뒤 다시 접속하는 비율이 gate_30에 해당하는 플레이어에 비해 통계적으로 높다고 할 수 없습니다.
3. gate_30에 해당하는 플레이어보다 gate_40에 해당하는 플레이어의 일주일 뒤 다시 접속하는 비율이 더 높을 것이다.
ab %>% group_by(version, retention_7) %>% count() %>%
ggplot(aes(x=version, y=n, fill=retention_7)) + geom_bar(stat = "identity", position = "dodge") + geom_text(aes(label = n), size = 10)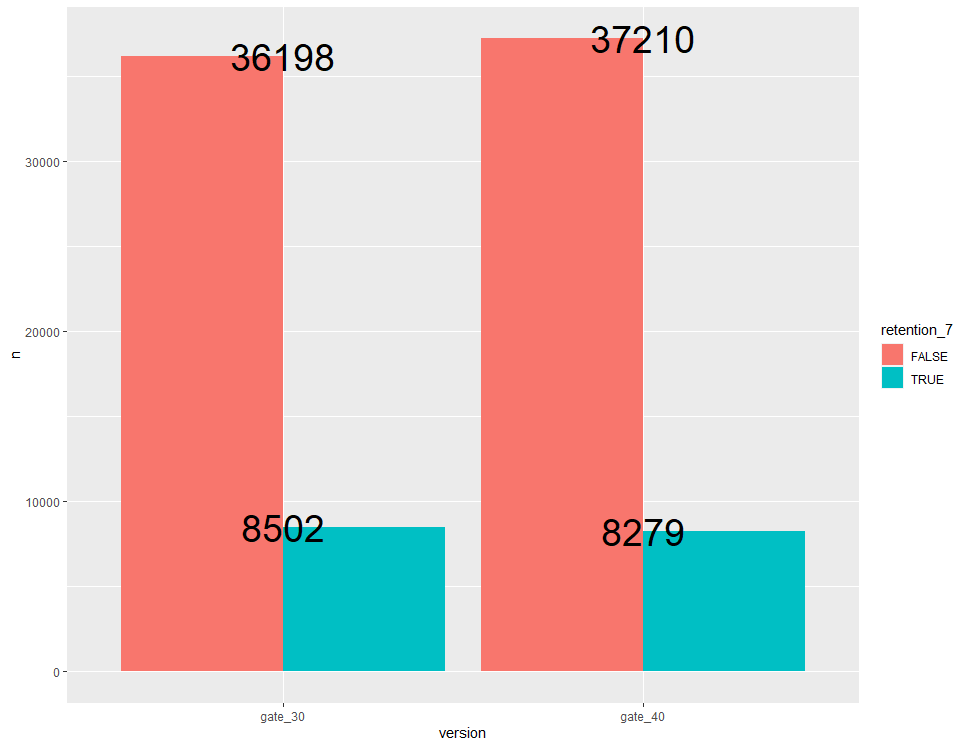
이번 가설검정 역시 목표변수가 이항 분포의 범주형 변수이기 때문에 version과 retention_7 변수로 구성된 table 표를 만들겠습니다.
addmargins(table(ab$version, ab$retention_7), margin = 2) FALSE TRUE Sum gate_30 36198 8502 44700
gate_40 37210 8279 45489
역시 마찬가지로 저희가 관심 있는 부분은 각 그룹에서 TRUE(일주일 뒤에 다시 접속한 플레이어의 수)의 비율이기 때문에 prop.test() 함수를 통해 두 그룹의 모비율 차이에 대한 검정을 수행하겠습니다.
prop.test(x=c(8502, 8279), n=c(44700, 45489), alter = "less")2-sample test for equality of proportions with continuity correction
data: c(8502, 8279) out of c(44700, 45489)
X-squared = 9.9591, df = 1, p-value = 0.9992
alternative hypothesis: less
95 percent confidence interval:
-1.00000000 0.01248696
sample estimates:
prop 1 prop 2
0.1902013 0.1820000
검정 결과 p-value가 0.9992로 0.05보다 매우 크기 때문에 귀무가설을 채택합니다.
즉 gate_40에 해당하는 플레이어가 일주일 뒤 다시 접속하는 비율이 gate_30에 해당하는 플레이어에 비해 통계적으로 높다고 할 수 없습니다.
A/B test의 결과를 최종적으로 정리하자면 gate_30 버전에 비해 gate_40 버전의 2주 동안 평균 게임 플레이 횟수, 하루 뒤 다시 접속하는 비율, 일주일 뒤 다시 접속하는 비율 모두 통계적으로 높다고 할 수 없는 결과가 나왔습니다.
이는 다시 말해 수정한 버전이 여러 지표들의 향상에 유의한 영향을 미치지 못했음을 의미하며, 따라서 기존의 A버전을 유지하던지 혹은 B버전에 사용된 수정 사항들 대신 다른 수정을 계획하는 것이 합리적이라고 판단됩니다.
이상으로 Cookie Cats 데이터셋을 활용한 A/B test 연습을 마치겠습니다. 감사합니다.
