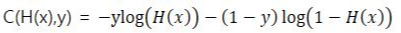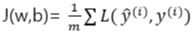이번에는 Logistic Regression이 무엇인지 배워보았습니다. 이전에 배웠던 Superviced Learning의 BinaryClassification의 대표적인 예로 이미지 분류가 있었습니다.
한 사진을 가지고 고양이인지 아닌지 Binary Classification을 하는 과정에 대해 설명할 것입니다.
Binary Classification
컴퓨터는 이미지를 Pixel의 RGB값을 데이터로 받아옵니다. 컴퓨터 화면은 많은 화소들로 구성되어있으며, 각 화소에는 빛의 3원색인 Red,Green,Blue로 조합을 하여 수많은 색을 만들어낼 수 있는 것입니다.
RGB값은 (0,0,0)부터 (255,255,255)까지 있으며 이 숫자는 빛의 세기를 의미합니다.
(255,255,255)는 흰색이 됩니다. RGB의 경우 세 가지 채널의 조합이고, 무채색 같은 경우 한 개의 채널이 존재합니다.
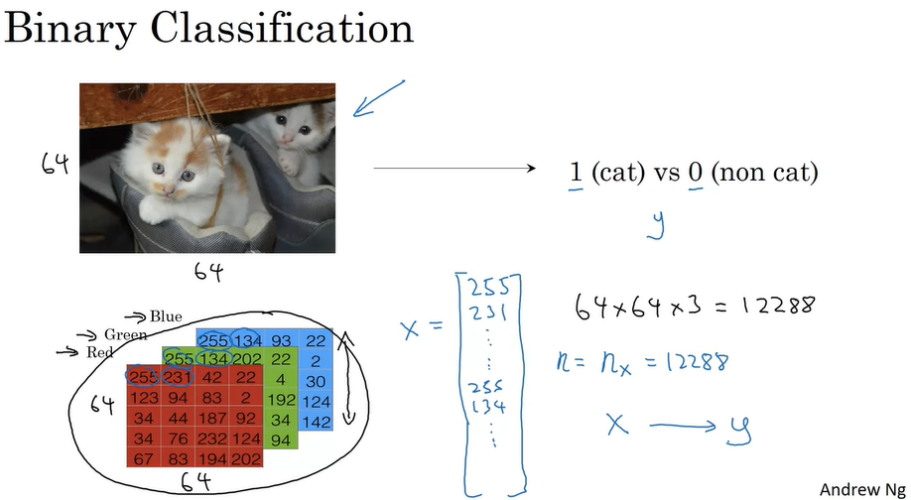
모니터에 64×64개의 픽셀이 있다고 하면 R,G,B 라는 세 개의 채널이 있고, 컴퓨터는 이미지를 인식할 때 각 화소의 출력값을 인식합니다. 이 때 각화소의 출력값은 n_x by 1의 Matrix로, 즉 1-D Array로 저장됩니다. (Red-Green-Blue 순으로)
이 개념을 기억하면서 Logistic Regression에 대해 살펴볼 것입니다.
딥러닝이란 (x,y)로 묶인 Trading data를 주고 컴퓨터가 f(x)를 계산하도록 하는 것인데,
이 때 input값인 x를 feature라 하고, output값인 y를 label이라고 하겠습니다.
이 경우 label은 y그 자체를 고양이인지의 여부가 되는 것이고, class는 y값의 종류로 1(Cat) 0(Non-cat) 2가지가 있는 것 입니다.
class가 두 개만 있어서 binary classfification가 되는 것입니다.
고양이 그림에서 64×64개의 픽셀이 있고 각 픽셀당 R,G,B의 3가지 값이 있기 때문에 12288개의 input data가 생기고, 이 12288개의 숫자는 12288 × 1 matrix로 저장이 되고 이 값은 feature의 개수로 n_x로 표기됩니다.
그러면 Training data가 많아진다면 어떤 식으로 표기가 될까요?
지금까지는 1개의 이미지 값에 대한 픽셀 데이터를 1-D array로 표현되는 것을 보았지만, m개의 Training data가 있는 경우, 즉 고양이 사진이 m장 있는 경우를 생각해보겠습니다.
-표기법(Notation)-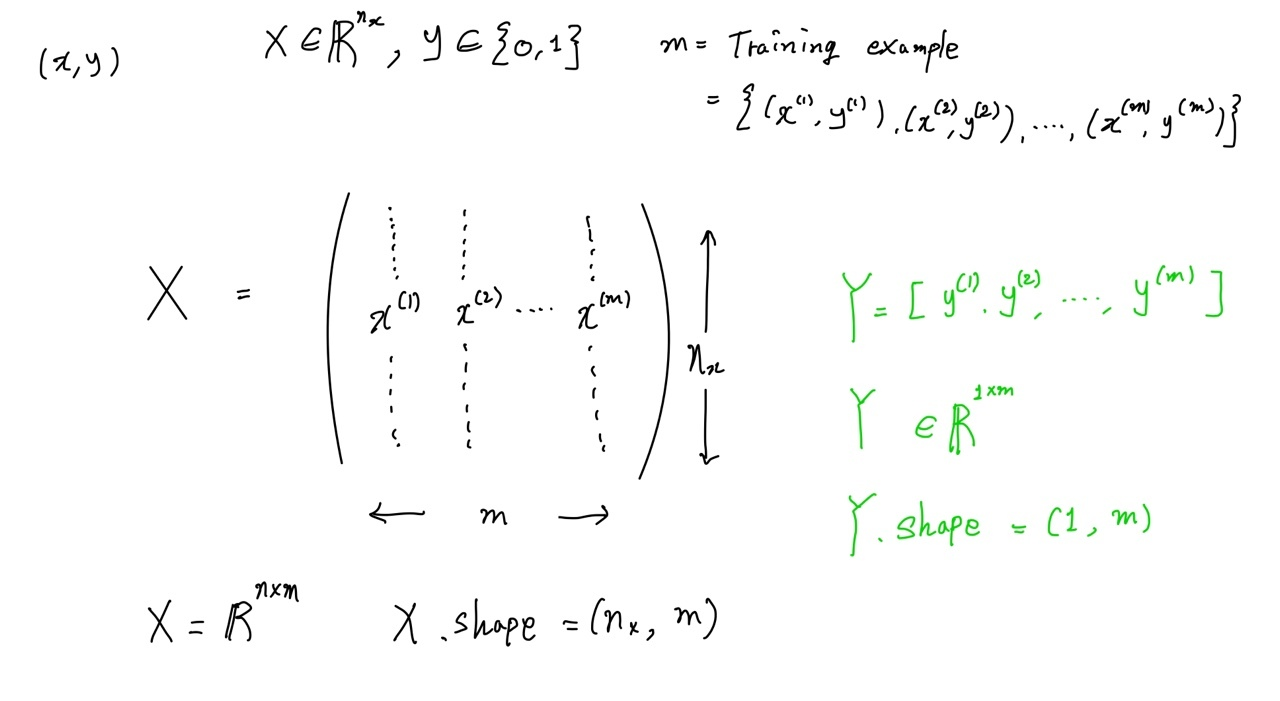
- Training Set이나 Test Set을 표시하기 위해 m{train},m{test}로 쓰기로 합니다.
- 모든 입력 x를 나타내기 위한 행렬을 대문자 x로 표기합니다.
- 출력 label y또한 행렬로 나타내며 대문자 Y로 표기합니다.
Logistic Regression의 5개 Setp
① Initialization
② Forward Propagation
③ Compute cost function
④ Backward Propagation
⑤ Gradient Descent
앞의 예시처럼 고양이를 판별할 때 feature값으로 한 개의 pixel값만 받아들이고 output으로 고양이인지의 결과가 출력되는데요. 여기에 한 가지 전제를 덧 붙이면 이해하기 쉬운 상황을 만들 수 있는데, 실제 고양이인지 판단하는 기준이 있다고 가정해봤습니다. 즉, 모든 고양이 사진은 실제로 100이 넘는 X값을 가지고 있다고 가정해봤습니다.

고양이 사진은 이 분포를 분포를 따릅니다. 그리고 딥러닝은 100이라는 기준값을 찾아내는 것이다. 그러기 위해 어떤 함수가 모델링 되는 메커니즘이 Logistic Regression이라고 할 수 있습니다.
1. Initialization (임의의 w,b값 설정)
실제로는 다변수 함수지만 w,b에만 의존하는 최적의 직선을 찾는다고 했을 때 그 최적의 직선이 되는 일차 함수를 z=f(w,b)=wx+b라고 해봅시다. 여기서 w,b의 값을 찾아주는 작업이 Initializtion입니다. (0,0)으로 잡을 경우 zero initailization이라고 하며, initailization을 어떻게 하는지에 따라 모델의 효율이 달라집니다.

z1은 zero initialization의 경우인데요. Logistic Regression을 통해 w,b값을 개선시켜 나갑니다.
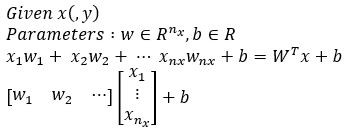
하지만 W^Tx + b의 치역이 0과 1을 넘기 때문에 밑의 자료 중에 Sigmoid라는 Activation Function으로 0과1 사이로 제한해줍니다.
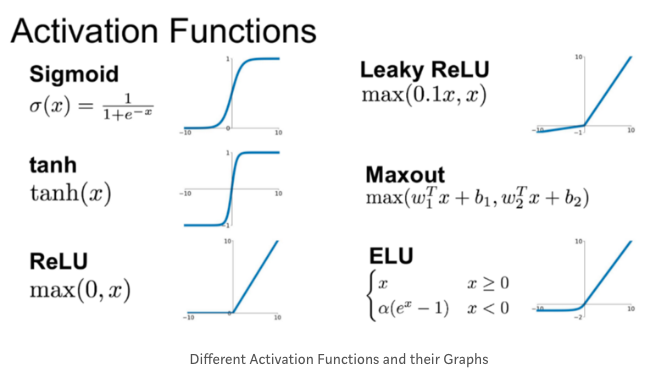
Sigmoid 함수는 0~1사이의 값만 다뤄지므로 Chain rule을 이용해 계속 값을 곱해나간다고 했을 때 0에 수렴할 수 밖에 없다는 한계를 가지고 있는데요. 그러므로 1보다 작아지지 않게 하기 위한 대안으로 ReLU라는 함수가 널리 사용되고 있습니다.
2.Forward Propagation
(Y_hat의 설정 == 가설 설정 -> 신경망의 출력값을 계산)
Initialization의 과정에서는 치역이 실수 전체인 점과, 실제 y값이 0 또는 1로 discrete하지만 z값은 continuous하다는 점이 문제가 있습니다.
치역의 문제는 앞서 언급했듯이 Sigmoid function으로 치역을 0~1사이로 만들어 해결할 수 있었습니다.
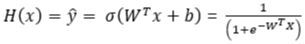


Sigmoid function은 위와 같으며 z를 넣어서 치역을 맞춥니다. (y_hat은 고양이인지 아닌지 추측하는 확률함수가 된다)
z가 Continuous한 점은 y_hat이 0.5미만일 경우는 0, 이상일 경우는 1로 반올림을 통해 해결할 수 있습니다.
3. Compute the cost function (loss function의 평균이 cost function)
y_hat을 구했다면 확률모델이 좋은 모델인지 cost function을 통해 판단해야합니다.(w,b값이 적절한지 판단합니다.)
어떤 function을 사용하는지에 다라 달라질 수 있는데요. MSE(Mean Square Error)를 사용하면 문제가 생깁니다.
이것은 Non-Convex function이기 때문에 global minimum을 보장하지 않습니다.
그러므로 Losgistic Regression은 Binary Cross Entrophy를 Cost Function으로 사용하게되는 것입니다.
Loss(error) function [1개]
Cost function [m개]
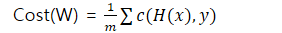
J = Cost Function, L = Loss function
4. Backward Propagation(기울기 계산)
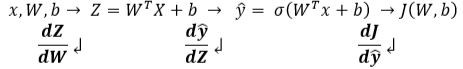
Cost Function으로 Binary Cross Entrophy를 사용해 구하고, Gradient Descent를 구하면 됩니다. 하지만 chain rule을 이용해 dJ/dw를 구해야하는데 그 과정에서 Backward Proagation단계가 진행됩니다.
이로써 forward propagation과 backward propagation이 왜 진행되는 것인지 알 수 있었습니다. 이후 마지막 단계로 Gradient Descent 과정을 반복하면 w,b값의 최솟값을 정할 수 있게 됩니다.
5. Gradient Descent
해당 함수의 최소값 위치를 알아내기 위해 Cost function의 기울기를 조금씩 이동하여 Optimal Parameter를 찾으려는 방법입니다.
여기서 기울기는 파라미터에 대해 편미분한 벡터를 의미하며 이 파라미터를 반복적으로 조금씩 움직이며 찾는 것입니다.
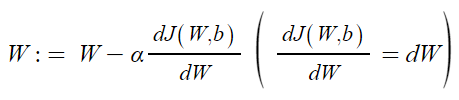
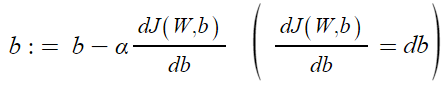
Logistic Regression derivatives (단일 샘플만)
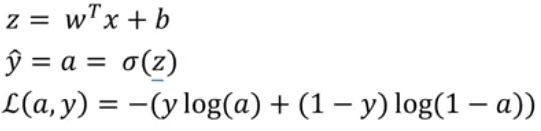
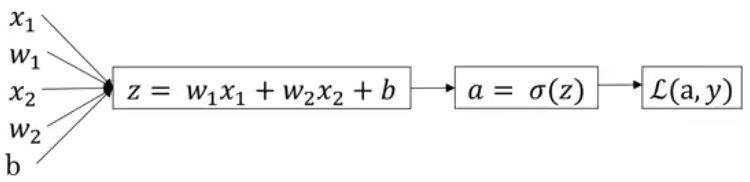
-
Step 1) 손실함수 L(a,y)의 도함수 구하기
- 역방향으로 가서 a에 대한 손실 함수의 도함수를 계산합니다.
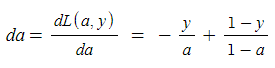
- 역방향으로 가서 z에 대한 손실 함수의 도함수를 계산
- 역방향으로 가서 a에 대한 손실 함수의 도함수를 계산합니다.
-
Step 2) w,b를 얼마나 바꿔야 하는 지 계산
- 단일 샘플에 대해 Gradient descent사용
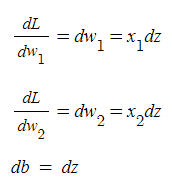
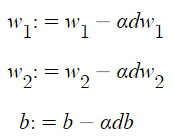
Gradient descent on m examples
위의 계산식을 적용하여 n개의 예제를 학습할 때 (n=2) :
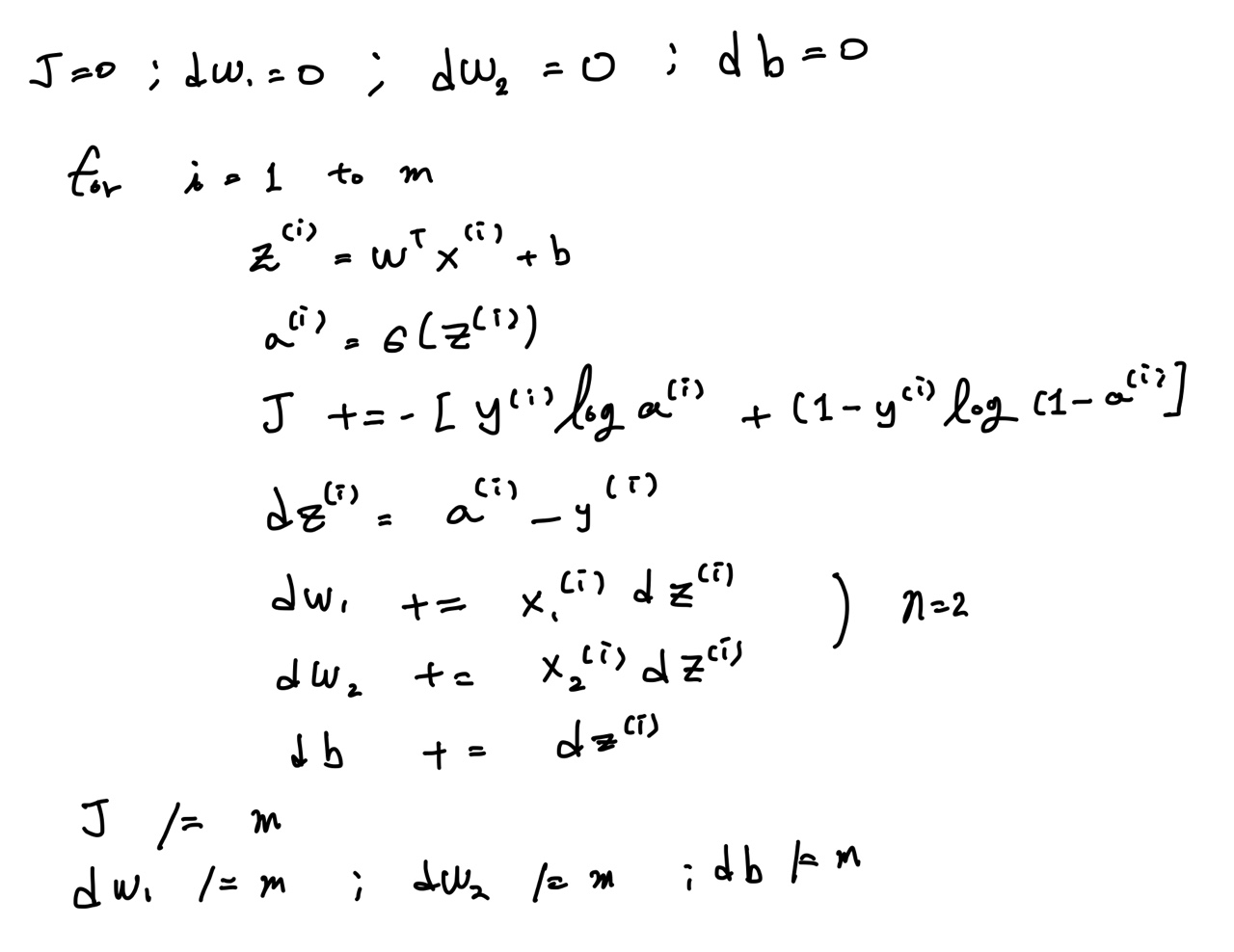
하지만 n이 많이 커지게 될 때(feature의 개수 증가) 중첩 for문을 써야하는 문제가 생깁니다.
그러므로 코드가 알고리즘을 비효율적으로 만들어 속도도 느려지는데요. 이 문제점을 위해 Vectorization이라는 개념이 필요합니다.
Vectorization
for문을 사용하면 코드의 양도 늘며 속도까지 느려집니다.
그러므로 행렬의 연산으로 변환하여 여러개의 연산을 한번에 진행하도록 하게 합니다. (Numpy를 사용)

이외에도 Numpy를 이용해 간단한 연산과 for문을 vectorization으로 변경하여 사용하면 연산시간이 얼마나 차이나는지 등을 비교해볼 수 있습니다.