직선

• 아핀 공간에서 점의 조합
  아핀 공간에서는 점과 점의 연산은 불가능했는데,
  두 스칼라 값 a, b를 점들에 각각 곱하여
  마지막 차원 값인 a+b가 1이 된다면 사용할 수 있다.
  $P(a) = a \cdot P1 + (1-a) \cdot P2$

• 아핀 조합
  모든 계수의 합이 1인 n 개의 스칼라 값을 사용한 점의 조합

이미지 출처

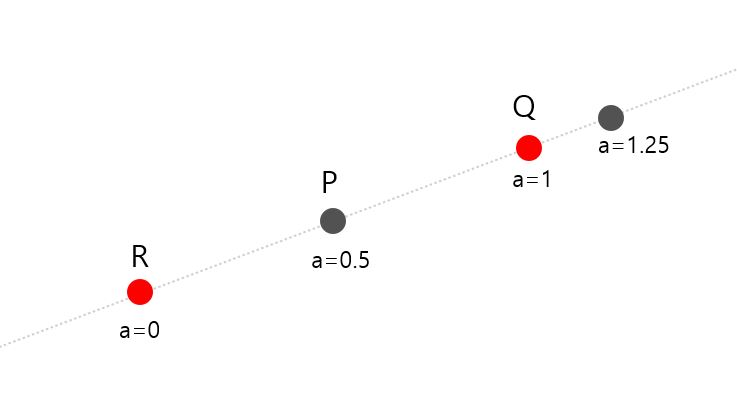
계수에 따라 무한한 점들이 직선을 만들어 냄

• 선의 종류
  직선 (Line) $-\infty < a < \infty$
  반직선 (Ray) $0 <= a < \infty$
  선분 (Line segment) $0 <= a <= 1$

스크린 좌표계

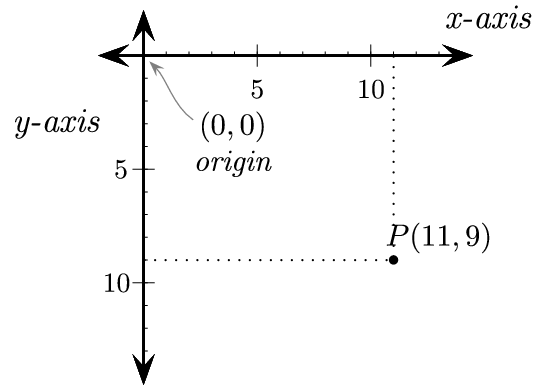
이미지 출처

• 특징
  양의 정수 H
  왼손 좌표계(우하방향 증가)
  이산성

픽셀화 (Rasterization)
물체의 형상을 픽셀로 변환해 표현

픽셀화 규칙
해상도가 짝수일 때, 원점 등의 점을 어떻게 찍을 것인가,
픽셀을 벡터로 변환할 때, 픽셀 영역의 대표값은 어디로 할 것인가 등

---

• 선 그리기 알고리즘
  (브레젠험, mid-point)
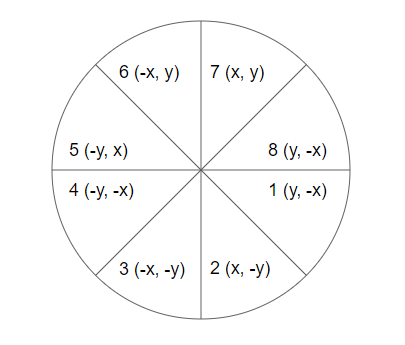
  좌표계를 8분면으로 나눠 분면마다의 기울기 특징을 이용

직선의 방정식
y = ax + b

스크린 좌표계에서 두 점이 주어졌을 때 다음 정보들을 얻을 수 있음
너비 (width) x1 - x0
높이 (height) y1 - y0
시작점 x0, y0

$y0 = (h/w)x0 + b \\ b = y0 - (h/w)x0$

1팔분면은 기울기가 1을 넘을 수 없음 => 평행 이동이나 1칸 아래로만 이동
직선의 방정식 우변이 좌변보다 낮으면 위 픽셀(평행 이동), 크면 아래 픽셀을 칠한다.

판별식을 정리하면 2h - w 가 된다.
판별식이 0보다 작을 시 평행이동, 클 시 아래 이동을 한다.
평행 이동 시 2h를 증가시키고, 아래 이동 시 2h-2w만큼 증가시킨다.

이를 시작점에서 끝점에 도달할 때까지 반복하는 것이 알고리즘이다.

2팔분면은 x가 증가하지 않고 y를 증가시키는 방향으로 전개
x와 y를 바꾼 상태로 동일하게 진행 판별식은 2w - h

남은 3 ~ 8팔분면은 경사와 x, y 방향에 따라

1팔분면 판별식을 쓰고 +-를 바꾸거나 2팔분면 판별식을 쓰고 +-를 바꾸어서 표현할 수 있음