게임수학강의
1.수의 구조

왜 수에 대해 알아야 하지?\-> 게임 세계는 벡터로 구성되고, 이 벡터는 수로 만들어져 있음\-> 수를 이해해야 시스템을 이해할 수 있다.실수 집합 R수 사이에 빈틈 없이 연속된 무한의 요소들로 구성된 수의 집합수의 직선실수 집합 R의 요소들을 점으로 나열하면 연속한
2.함수

게임은 대부분 화면을 통하여 새로운 공간을 보여주고,이를 위하여 공간과 공간의 변환이 이루어짐이러한 공간 변환을 설명하는 이론이 함수라고 할 수 있음함수집합 X의 모든 요소가 집합 Y에 1:N 대응정의역 (Domain)집합 X공역 (Codomain)집합 Y치역 (Ran
3.벡터

수 직선의 확장데카르트 좌표계 (Cartesian Coordinate system)두 실수 집합을 직교하도록 교차시켜 평면을 표현R $\\times$ R의 원소를 좌표 (x, y)라 표현 벡터체 집합 F의 곱집합을 벡터공간 V라하고 이 스칼라의 순서쌍인 원소를 벡터라
4.선형독립

선형 조합 (Linear combination)벡터의 기본 연산을 사용해 새로운 벡터 생성선형 의존(종속)선형 조합으로 새로운 벡터를 생성할 때 0이 아닌 계수로 0 벡터를 만들 수 있는 경우선형 독립선형 조합으로 새로운 벡터를 생성할 때 0 벡터를 만들려면 계수가 0
5.삼각함수

직각삼각형의 삼요소밑변 높이 빗변삼각비sin, cos, tan삼각함수삼각비를 집합의 관점에서 함수로 나타낸 것정의역: 실수 집합공역: -1 ~ 1삼각함수의 성질사인 함수는 축을 기준으로 포개면 반대 값을 가지게 됨코사인 함수는 축을 기준으로 대칭으로 값이 같음탄젠트 함
6.선형성

선형성가산성과 1차 동사성을 모두 만족 시가산성: f(x+y) = f(x) + f(y)1차 동사성: af(x) = f(ax)=> y = axy = ax + b 일 경우 만족하지 않음=> b라는 인자가 순수한 1차 비례 관계를 깨버림사상 (Mapping)함수: 집합과 집
7.행렬
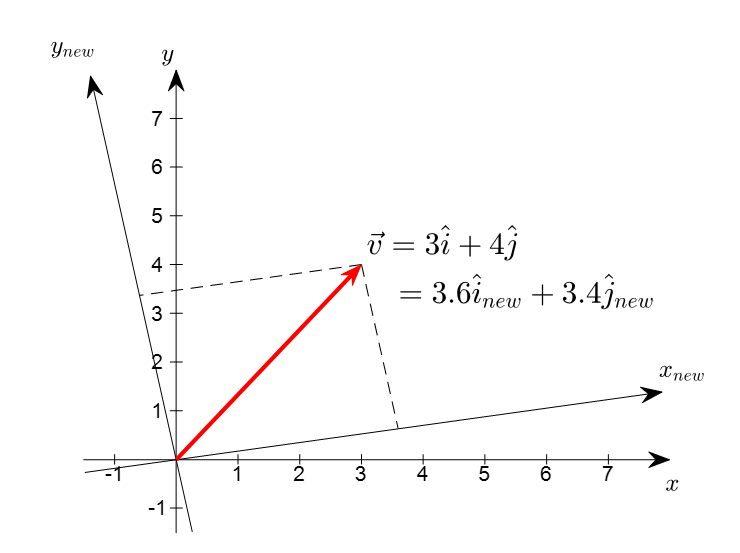
행렬수를 행과 열에 맞춰 배열=> 선형 변환의 표현행과 열의 수가 같은 행렬 : 정방 행렬행렬은 결합, 분배 법칙을 만족하지만 교환 법칙을 만족하지 않음행렬 곱의 전치 연산$(A \\cdot B)^T = A^T \\cdot B^T$선형 변환과 행렬정방 행렬 M = $\
8.역행렬

항등 행렬 (Identity matrix)선형 변환의 결과가 변함없는 행렬$I = \\begin{bmatrix} 1 & 0 \\ 0 & 1 \\end{bmatrix}$역행렬선형 변환된 결과를 거꾸로 돌려주는 선형 변환변형전 행렬과 역행렬을 곱할 시 항등 행렬이 나온다.
9.아핀 공간

이동 변환의 문제점원점에서부터 시작하는 벡터의 특성상 기저벡터를 원점으로부터 분리해 이동시킬 수 없음밀기 변환의 활용2차원에서 밀기 변환 시 기저 벡터와 평행한 벡터는 1차원적으로 이동하게 된다.=> 3차원에서 밀기 변환 시 평면 이동이 가능해짐3차원 정방 행렬을 통한
10.내적

벡터의 연산벡터와 벡터의 곱(a,b,c) $\\cdot$ (d,e,f) = (ad, be, cf)벡터의 내적(a, b) $\\cdot$ (c, d) = ac + bd벡터의 외적 (3차원 한정)벡터 내적의 성질교환, 분배 법칙이 성립하지만 결합 법칙은 성립하지 않음벡터
11.직선
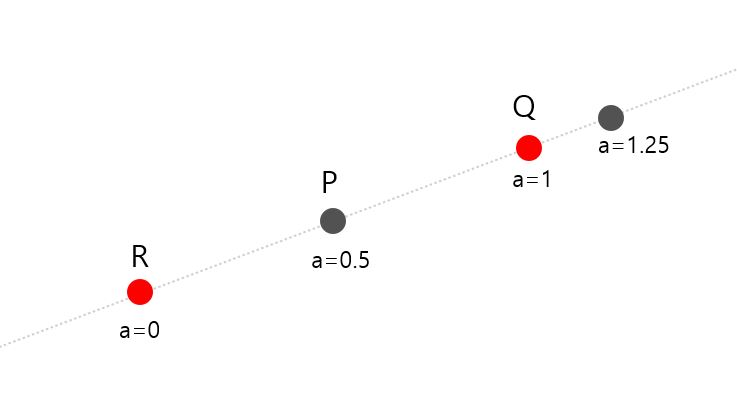
아핀 공간에서 점의 조합아핀 공간에서는 점과 점의 연산은 불가능했는데,두 스칼라 값 a, b를 점들에 각각 곱하여 마지막 차원 값인 a+b가 1이 된다면 사용할 수 있다.$P(a) = a \\cdot P1 + (1-a) \\cdot P2$아핀 조합모든 계수의 합이 1인
12.삼각형
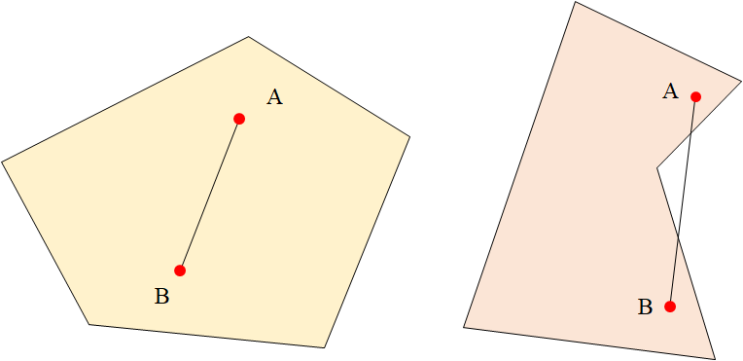
세 점의 아핀 조합$P = s \\cdot P1 + t \\cdot P2 + (1-s-t) \\cdot P3$$P - P3 = s(P1 - P3) + t(P2 - P3) \\\\vec{w} = s\\vec{u} + t\\vec{v}$벡터 u와 v가 선형 독립이라면세 점
13.텍스쳐 매핑
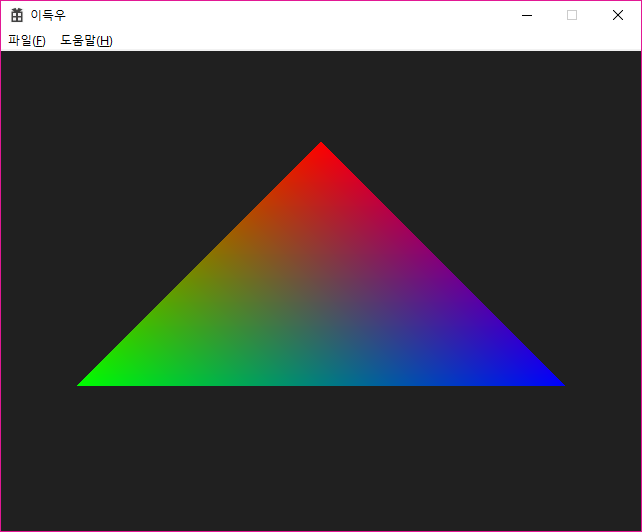
삼각형 칠하기무게중심 좌표 (1-s-t, s, t)P1과 P2, P3는 모두 0.333$\\cdots$의 영향력을 가지고 있음메시 구조 데이터에서 정점 버퍼에 색상 정보를 추가좌표마다 색상이 영향력에 따라 정해짐이미지 출처텍스쳐 매핑이미지(텍스쳐)를 불러들여 삼각형을
14.게임 엔진

로컬 공간과 월드 공간여러 점들이 모여 하나의 물체를 생성물체는 (0,0,1)을 중심으로 상대적인 위치로 나타내어 짐이 물체를 그리는데 사용하는 공간을 로컬 공간(Local space)이라고 함게임은 플레이어가 움직이며 공간을 탐험하는데 이 별도의 공간을 월드 공간(w
15.뷰 공간

뷰 공간플레이어가 월드 공간을 탐험할 때, 일정한 영역을 모니터에 표현해야 한다.월드 공간의 일부를 화면에 보여주기 위해 재배치한 공간을 뷰 공간이라 한다.한마디로 뷰 공간은 화면을 찍는 카메라를 원점으로 월드 공간을 재배치한 공간이다.월드에 배치된 오브젝트 좌표가 뷰
16.3차원 공간
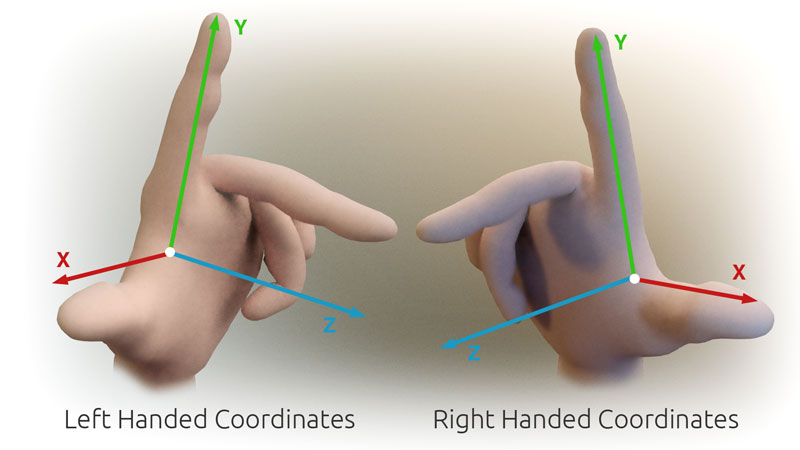
왼손, 오른손 좌표계이미지 출처왼손 좌표계는 모니터 기준 안쪽이 +축이고, 오른손 좌표계는 바깥쪽임위로 향하는 방향은 시선 벡터로부터 회전 행렬을 만들 때 참고하기 때문에일반적으로 z축 방향과 Up 방향을 정하여 좌표계를 규정이미지 출처3차원 트랜스폼2차원의 트랜스폼을
17.오일러각

오일러각x, y, z 로컬 기저 축을 중심으로 축마다 회전된 각도 가짐$R = ( \\theta_x , \\theta_y, \\theta_z)$기존 회전 행렬을 가지고 나타낼 때는 9개의 데이터가 필요했고 이를 대체yaw, roll, pitch오른손 좌표계 기준 y,
18.외적

외적3차원 벡터에서 이뤄지는 연산결과값으로 벡터가 나옴$u=(u_x,u_y,u_z),\\ v=(v_x,v_y,v_z)$$u\\times v=(u_yv_z-v_yu_z,\\ u_zv_x-v_zu_x,u_xv_y-v_xu_y)$분배 법칙만 성립하고 교환, 결합 법칙이 성립
19.원근 투영

원근 투영세상은 3차원이지만 눈은 사각뿔 형태로 세상을 바라본다고 생각할 수 있다.해당 공간에서 평면의 크기는 카메라로부터의 거리에 따라 달라진다.이 때 눈과 평면의 거리를 초점거리라고 하고, 평면은 투영 평면이라 한다.NDC (Normalized Device Coor
20.깊이 값

깊이 값의 필요성3차원 공간에서 다수의 물체를 그릴 때, 그리는 순서를 고려하지 않으면나중에 그려지는 물체가 먼저 그려진 물체보다 무조건 앞에 그려지게 됨절두체 (Frustum)카메라로 만들어지는 사영 공간의 z 값에 범위를 설정하여사각뿔에서 꼭지가 잘라진 육면체를 만