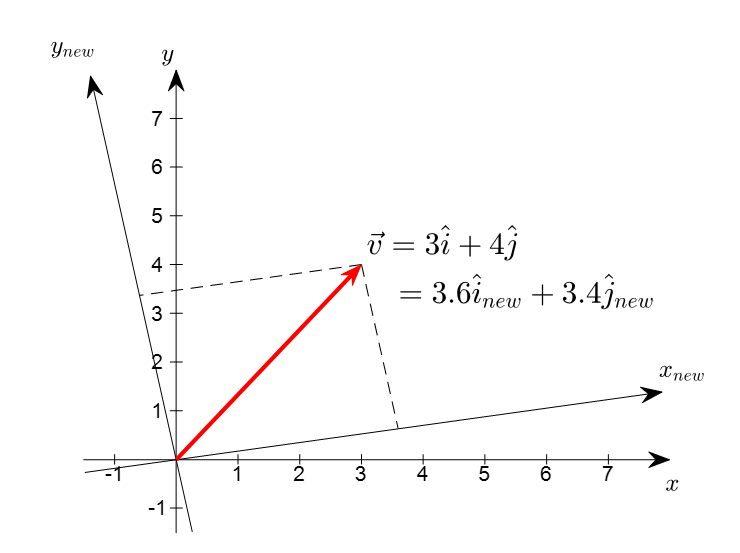
행렬

행렬
수를 행과 열에 맞춰 배열
=> 선형 변환의 표현

행과 열의 수가 같은 행렬 : 정방 행렬

행렬은 결합, 분배 법칙을 만족하지만 교환 법칙을 만족하지 않음

행렬 곱의 전치 연산
$(A \cdot B)^T = A^T \cdot B^T$

---

선형 변환과 행렬

정방 행렬 M = $\begin{bmatrix} a & b \\ c & d \end{bmatrix}$

열벡터 v = $\begin{bmatrix} x \\ y \end{bmatrix}$

M $\cdot$ v = $\begin{bmatrix} ax + by \\ cx+dy \end{bmatrix}$

=>

f(x, y) = (ax + by, cx + dy)

정방 행렬은 같은 차원의 공간이 서로 대응되는 선형 변환을 의미
열벡터는 벡터 공간의 벡터를 의미

열기반 행렬 (Column major matrix)
OpenGL, 수학에서 사용하는 기본 방식

행기반 행렬 (Row major matrix)
DirectX 및 게임 엔진에서 사용하는 방식

$\begin{bmatrix} x & y \end{bmatrix} \cdot \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} ax + by & cx+dy \end{bmatrix}$

열기반과 행기반은 전치 관계일 뿐 결과는 동일

---

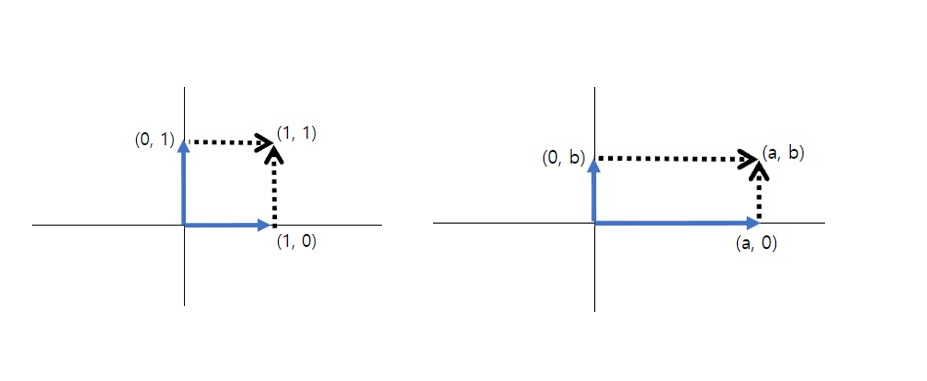
원 벡터 공간의 선형 변환
(x, y) = x(1, 0) + y(0, 1)

=> $\times\begin{bmatrix} a & b \\ c & d \end{bmatrix}$

x(a, c) + y(b, d) = (a + b, c+ d)

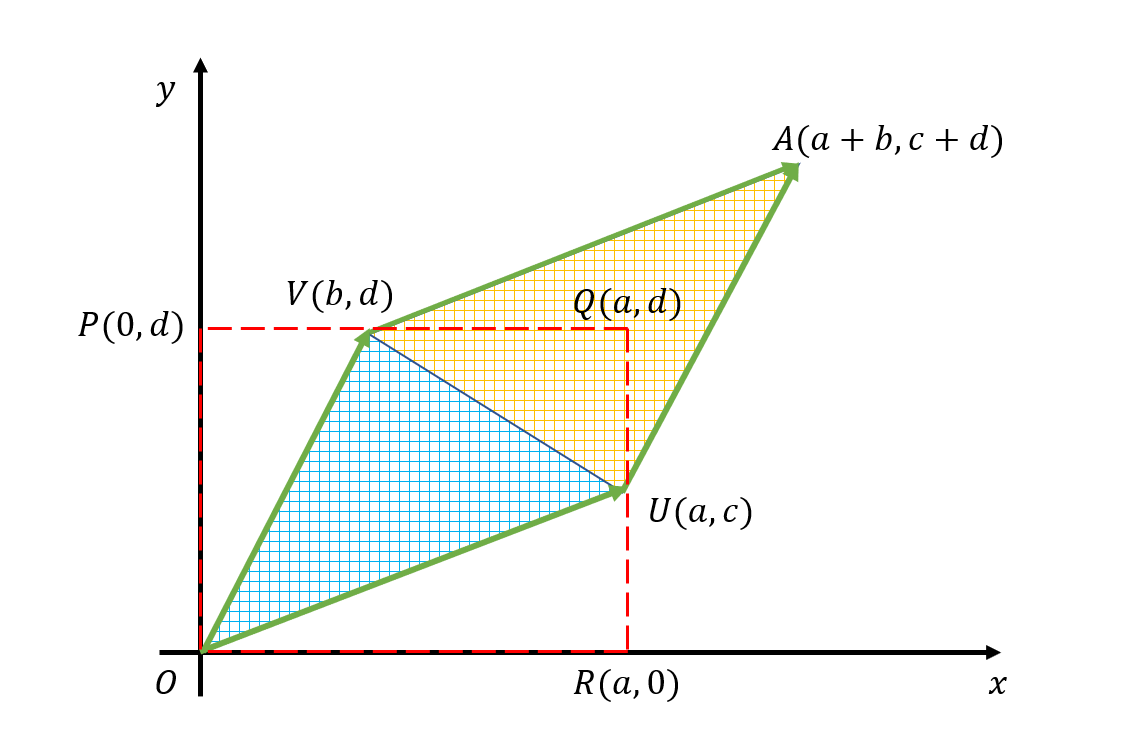
이미지 출처

선형 변환된 첫번째 표준 기저 벡터 e1 = (a, c)
선형 변환된 두번째 표준 기저 벡터 d2 = (b, d)
$\begin{bmatrix} \begin{pmatrix}a \\ c \end{pmatrix} \begin{pmatrix}c \\ d \end{pmatrix} \end{bmatrix}$

---

크기 변환

$\times\begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix}$

밀기 변환
$\times\begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix}$

90도 회전(시계)
$\times\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$

90도 회전(반시계)
$\times\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$

임의의 각도 $\theta$만큼 회전
$\times\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$

---

행렬의 곱

두 행렬을 곱한 식 ($A \cdot B$)는 벡터 공간 V에서 벡터 공간 W로 직행하는 합성 변환을 의미하며, 함수 $A \circ B$와 동일하다.

삼각함수 합의 공식을 회전 행렬 2개의 곱으로 유도할 수 있음
(a각 회전 + b각 회전은 (a+b)각 회전으로 나타낼 수 있음)

주로 사용하는 선형 변환은 5가지이다
Scale(S), Ratoation(R), Translation(T), View(V), Projection(P)

변환이 고정되어 있다면 PVTRS를 미리 계산해두고 새로 들어오는 벡터와 곱해주기만 하면 된다.