Gradient Boosting Classifier

Introduction

Gradient Boosting Classifier is a powerful machine learning algorithm that belongs to the ensemble methods family, specifically to boosting techniques. It works by sequentially adding predictors (typically decision trees), where each one corrects its predecessor. Unlike other boosting methods that adjust the weights of observations, Gradient Boosting focuses on minimizing the loss function, a differentiable function that measures the error of the model.

Background and Theory

Gradient Boosting combines multiple weak learners (models that perform slightly better than random guessing) to create a strong learner in a sequential manner. The core principle is to construct new models that predict the residuals or errors of prior models and then add these new models to the ensemble.

Mathematical Foundations

Let's denote our data set as $(x_i, y_i)$, where $x_i$ represents the features and $y_i$ the target variable for the $i^\text{th}$ observation. The goal is to find a function $F(x)$ that maps input features $x$ to predictions as close as possible to the target values $y$.

The algorithm starts with a model that makes constant predictions:

where $L(y_i, \gamma)$ is the loss function evaluated at the initial prediction $\gamma$ and the true target value $y_i$.

At each stage $m = 1$ to $M$, where $M$ is the total number of trees, the algorithm fits a new model $h_m(x)$ to the negative gradient of the loss function evaluated at the previous model's predictions:

Then, it finds the best-fit model $h_m(x)$ to these residuals. The model $h_m(x)$ is typically a decision tree.

Next, it computes a multiplier $\gamma_m$ for the model $h_m(x)$ that minimizes the loss when added to the existing model $F_{m-1}(x)$:

The model is then updated:

where $\nu$ is the learning rate, a parameter that scales the contribution of each $h_m(x)$.

The process repeats for $M$ iterations or until a stopping condition is reached, resulting in a final model:

Algorithmic Contemplation

Let’s try generalizing the problem Gradient Boosting algorithm is about to solve. We want to find the function $\hat{F}\in\mathcal{H}$ which minimizes the expected loss function in terms of $p$-dimensional loss function $L$, where $\mathcal{H}=\{F\mid F:\mathbb{R}^p\rightarrow\mathbb{R}\}$.

Unfortunately, $\mathcal{H}$ is an enormous set for the algorithm to find optimal $\hat{F}$. Therefore, some constraints are needed, which constrains $\mathcal{H}$ to:

where $M$ is a natural number.

In short, a structure which can be expressed through a linear combination of a constant and several functions is added, rather than a simple generic function.

Moreover, since the distributions of $x,y$ are unknown, it is highly demanding to figure out the expected loss. Therefore, we have to find $\hat{F}$ that minimizes the experienced loss function, which can be derived by utilizing a finite amount of data $(x_i,y_i),~i=1,\ldots,n$.

This can be found by following several steps:

At this point, Gradient Boosting reforms the last equation by substituting the minimizing part with the gradient descent method as following:

$F_m$ can be approximated with respect to the positive integer $\gamma$. This is the reason why the term Gradient is included in the name of this boosting algorithm.

Here, the gradient can be computed as:

which in most cases(except for MSE loss), are very complitated to compute. Therefore, we take the 1st-order Taylor approximation with respect to $f_m$, which necessarily requires the loss function to be differentiable.

If we differentiate the right-hand term of the above equation with respect to $f_m(x_i)$, we can approximate the $\nabla L(y_i,F_{m-1}(X_i)+f_m(x_i))$ by:

And therefore:

Additionaly, we can optimize $\gamma$ in order to minimize the residuals:

As a result, we can define the pseudo-residual $r_{im}$ as following:

For the next step, we train a new function $g_m$, which accepts $x_i$ as an input variable and $r_{im}$ as an output variable, by approximating $r_{im}$ with respect to $x_i$. Then we can redefine $\gamma_m$ as following:

Consequently, $F_m$ can be finally set as $F_m(x)=F_{m-1}(x)+l\cdot\gamma_m\cdot g_m(x)$ by adopting $l$, which is for the prevention of overfitting.

From previous explanations, $h_i(x),~i=1,\ldots,M$ are in fact $\gamma_i\cdot g_i(x)$.

Loss Functions

In the Gradient Boosting Classifier, the choice of the loss function is crucial as it directly influences the model's performance by determining how well the predictions fit the actual data. Here are two popular loss functions and their mathematical integration into the algorithm:

Binary Cross-Entropy Loss

For a binary classification with target variable $y \in \{0,1\}$ and predicted probability $p = \sigma(F(x))$ where $\sigma(\cdot)$ is the sigmoid function, the Binary Cross-Entropy loss for a single observation is given by:

In the context of Gradient Boosting, the gradient (negative gradient of the loss with respect to $F(x)$) that we fit the next model to is:

where $p_i = \sigma(F_{m-1}(x_i))$ is the predicted probability based on the model at iteration $m-1$.

Multinomial Deviance Loss

For a classification problem with $K$ classes, let $y$ be the true class encoded as a one-hot vector $(y_1, y_2, \ldots, y_K)$, where $y_k = 1$ for the correct class and $y_j = 0$ for all $j \neq k$. Let $p_k = P(Y = k \mid X = x)$ be the predicted probability that observation $X = x$ belongs to class $k$. The Multinomial Deviance Loss for a single observation is given by:

The gradient of this loss function with respect to the model's output $F_k(x)$ for class $k$ is:

where $p_k = {e^{F_k(x)}}/{\sum_{j=1}^{K} e^{F_j(x)}}$ is the predicted probability for class $k$, computed using the softmax function over the outputs for all classes.

Exponential Loss

For a binary classification problem with target variable $y \in \{-1,1\}$ (note the difference in encoding compared to the binary cross-entropy loss, where targets are usually $0$ and $1$), and a prediction model $F(x)$, the Exponential Loss for a single observation is given by:

The negative gradient of this loss function with respect to the prediction $F(x)$, which is what the next model in the sequence will predict, is given by:

This formulation effectively weights the update of each point by how poorly it was predicted by the previous model: the worse the prediction (in terms of sign and magnitude of the margin $y F(x)$), the higher the weight of the corresponding point for the next model to focus on.

Procedural Steps

1. Initialization: Start with a constant model $F_0(x)$.
2. For $m = 1$ to $M$:
   • Compute the residuals $r_{im}$, the negative gradient of the loss function.
   • Fit a model $h_m(x)$ to these residuals.
   • Find the optimal multiplier $\gamma_m$.
   • Update the model $F_m(x) = F_{m-1}(x) + \nu \gamma_m h_m(x)$.
3. Output: The final model $F_M(x)$.

Implementation

Parameters

• base_estimator: Estimator, default = DecisionTreeRegressor()
  Base estimator for training multiple models
  
• n_estimators: int, default = 100
  Number of base estimators to fit
  
• learning_rate: float, default = 0.1
  Shrinking factor of the contribution of each estimator
  
• subsampling: float, default = 1.0
  Fraction of samples to be used for fitting each estimator
  

Examples

Test on standardized and reduced($\mathbb{R}^{n\times64}\rightarrow\mathbb{R}^{n\times2}$) digits dataset with only 5 classes:

from luma.ensemble.boost import GradientBoostingClassifier
from luma.preprocessing.scaler import StandardScaler
from luma.model_selection.split import TrainTestSplit
from luma.reduction.linear import KernelPCA
from luma.visual.evaluation import DecisionRegion, ROCCurve

from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import numpy as np

np.random.seed(42)

X, y = load_digits(n_class=5, return_X_y=True)
indices = np.random.choice(X.shape[0], size=500)

X_sample = X[indices]
y_sample = y[indices]

sc = StandardScaler()
X_sample_std = sc.fit_transform(X_sample)

kpca = KernelPCA(n_components=2, gamma=0.01, kernel='rbf')
X_kpca = kpca.fit_transform(X_sample_std)

X_train, X_test, y_train, y_test = TrainTestSplit(X_kpca, y_sample, 
                                                  test_size=0.3).get

gb = GradientBoostingClassifier(n_estimators=100,
                                learning_rate=0.1,
                                subsample=1.0,
                                max_depth=3)

gb.fit(X_train, y_train)

X_cat = np.concatenate((X_train, X_test))
y_cat = np.concatenate((y_train, y_test))

score = gb.score(X_cat, y_cat)

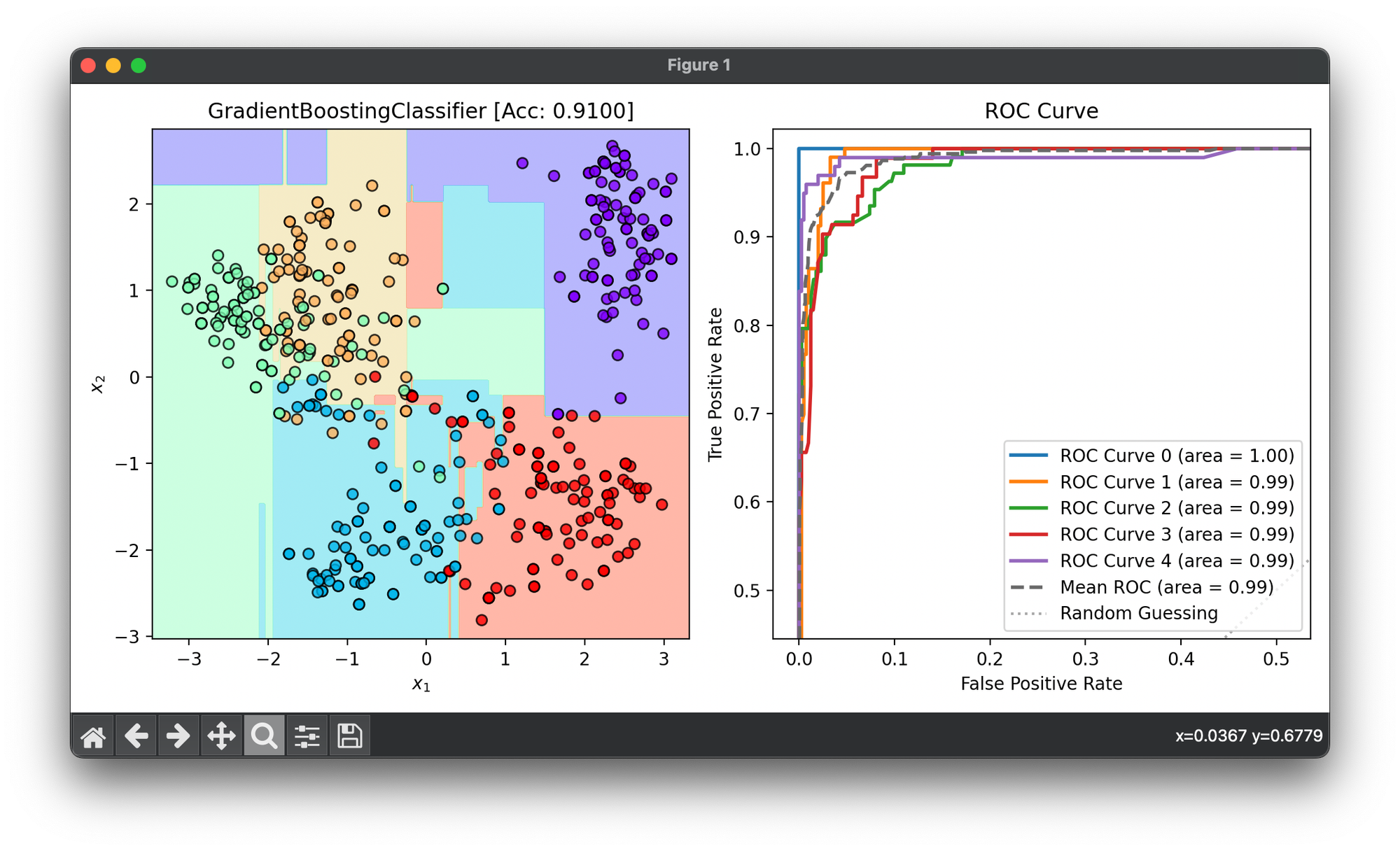
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

dec = DecisionRegion(gb, X_cat, y_cat)
dec.plot(ax=ax1)
ax1.set_title(f'GradientBoostingClassifier [Acc: {score:.4f}]')

pr = ROCCurve(y_cat, gb.predict_proba(X_cat))
pr.plot(ax=ax2, show=True)

Applications

Gradient Boosting Classifier is used in a variety of domains due to its flexibility and accuracy. Common applications include but are not limited to:

• Fraud detection in banking.
• Customer churn prediction.
• Disease outbreak prediction.
• Demand forecasting in retail.

Strengths and Limitations

Strengths

• Highly Accurate: Often provides very high accuracy across a wide range of applications.
• Flexibility: Can handle different types of data and is adaptable to various loss functions.

Limitations

• Prone to Overfitting: Especially with noisy data and without proper regularization.
• Computationally Intensive: Can be slower to train due to the sequential nature of boosting.
• Parameter Tuning: Requires careful tuning of parameters and stopping criteria to avoid overfitting and underfitting.

Advanced Topics

• Regularization Techniques: Techniques like shrinkage (learning rate) and stochastic gradient boosting can help prevent overfitting.
• Loss Functions: Beyond the typical use with classification and regression tasks, custom loss functions can be implemented for specific applications.

References

1. Friedman, J. H. (2001). "Greedy Function Approximation: A Gradient Boosting Machine." Annals of Statistics.
2. Natekin, A., & Knoll, A. (2013). "Gradient boosting machines, a tutorial." Frontiers in Neurorobotics.