Random Forest Classifier

Introduction

The Random Forest Classifier is a powerful and versatile machine learning algorithm used for classification tasks. It operates by constructing a multitude of decision trees at training time and outputting the class that is the mode of the classes (classification) of the individual trees. Random forests correct for decision trees' habit of overfitting to their training set, providing a more generalized model.

Background and Theory

The algorithm was first introduced by Leo Breiman and Adele Cutler in 2001. Random Forests belong to the ensemble learning family, which means they use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone.

A Random Forest Classifier builds multiple decision trees and merges them together to get a more accurate and stable prediction. The core concept behind random forests is the idea of "bagging" or Bootstrap Aggregating, where multiple models (in this case, trees) are trained on different parts of the same training set and then averaged to improve the stability and accuracy.

Mathematical Foundations

Each tree in the forest is built from a sample drawn with replacement (i.e., a bootstrap sample) from the training set. Additionally, when splitting a node during the construction of the tree, the split that is chosen is no longer the best split among all features. Instead, the split that is picked is the best split among a random subset of the features. As a result, the correlation between trees in the forest is decreased, leading to a decrease in the forest's variance without an increase in bias.

Procedural Steps

1. Bootstrap sampling: Randomly select N samples from the training data with replacement to create a subset of the data. This is done for each tree to be trained.
2. Tree building: For each bootstrap sample, grow a decision tree. At each node:
   • Randomly select $m$ features from the total features.
   • Choose the best split from these $m$ features to split the node.
   • Split the node into child nodes.
3. Repeat the process for a specified number of trees.
4. Voting for classification: For classification tasks, each tree votes, and the most popular class is chosen as the final outcome for the input data.

Mathematical Formulations

Given a training set $X = x_1, x_2, \ldots, x_n$ with corresponding labels $Y = y_1, y_2, \ldots, y_n$, a random forest classifier constructs a collection of decision trees $\{T_1, T_2, \ldots, T_k\}$, each trained on a bootstrap sample of the training data.

The prediction of the random forest, $f(x)$, for an input sample $x$ is given by:

where $\text{mode}\{\cdot\}$ denotes the statistical mode (i.e., the most frequent label among the predictions of the individual trees).

Implementation

Parameters

• n_trees: int, default = 100
  Number of trees in the forest
  
• max_depth: int, default = 10
  Maximum depth of each trees
  
• criterion: Literal['gini', 'entropy'], default = ‘gini’
  Function used to measure the quality of a split
  
• min_samples_split: int, default = 2
  Minimum samples required to split a node
  
• min_samples_leaf: int, default = 1
  Minimum samples required to be at a leaf node
  
• max_features: int, default = None
  Number of features to consider
  
• min_impurity_decrease: float, default = 0.0
  Minimum decrement of impurity for a split
  
• max_leaf_nodes: int, default = 1
  Maximum amount of leaf nodes
  
• bootstrap: bool, default = True
  Whether to bootstrap the samples of dataset
  
• bootstrap_feature: bool, default = False
  Whether to bootstrap the features of each data
  
• n_features: int Literal['auto'], default = ‘auto’
  Number of features to be sampled when bootstrapping features
  

Examples

Test on standardized and reduced($\mathbb{R}^{n\times64}\rightarrow\mathbb{R}^{n\times2}$) digits dataset with only 5 classes:

from luma.ensemble.forest import RandomForestClassifier
from luma.preprocessing.scaler import StandardScaler
from luma.model_selection.split import TrainTestSplit
from luma.reduction.linear import KernelPCA
from luma.visual.evaluation import DecisionRegion, ConfusionMatrix

from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import numpy as np

np.random.seed(42)

X, y = load_digits(n_class=5, return_X_y=True)
indices = np.random.choice(X.shape[0], size=500)

X_sample = X[indices]
y_sample = y[indices]

sc = StandardScaler()
X_sample_std = sc.fit_transform(X_sample)

kpca = KernelPCA(n_components=2, gamma=0.01, kernel='rbf')
X_kpca = kpca.fit_transform(X_sample_std)

X_train, X_test, y_train, y_test = TrainTestSplit(X_kpca, y_sample, 
                                                  test_size=0.3).get

forest = RandomForestClassifier(n_trees=10,
                                max_depth=100,
                                criterion='gini',
                                min_impurity_decrease=0.01,
                                bootstrap=True)

forest.fit(X_train, y_train)

X_cat = np.concatenate((X_train, X_test))
y_cat = np.concatenate((y_train, y_test))

score = forest.score(X_cat, y_cat)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

dec = DecisionRegion(forest, X_cat, y_cat, cmap='Spectral')
dec.plot(ax=ax1)
ax1.set_title(f'RandomForestClassifier [Acc: {score:.4f}]')

conf = ConfusionMatrix(y_cat, forest.predict(X_cat), cmap='BuPu')
conf.plot(ax=ax2, show=True)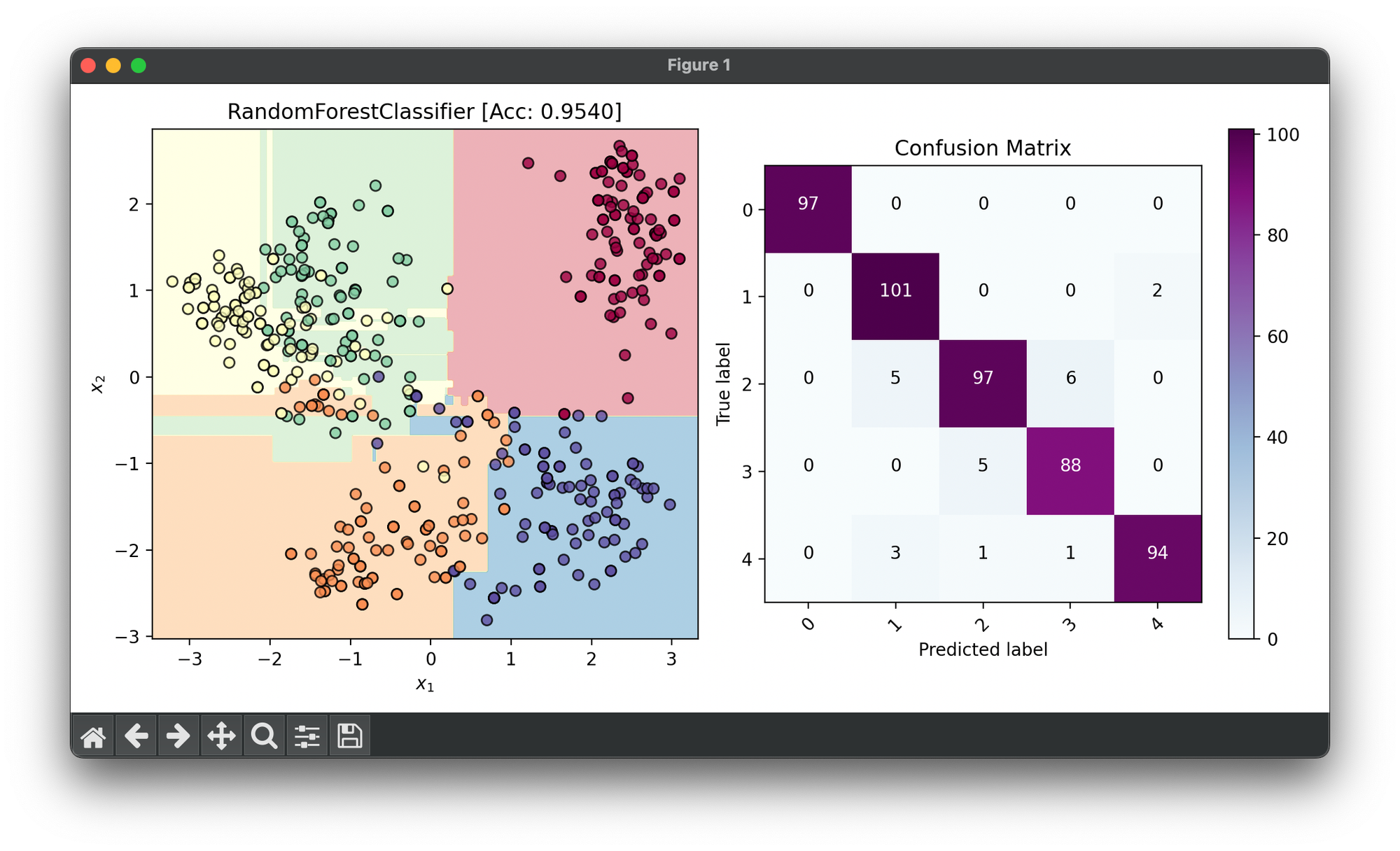

Applications

• Medical Diagnosis: Random Forests are used for diagnosing diseases by analyzing patient data.
• Financial Market Analysis: They can predict stock market movements by analyzing historical data.
• E-Commerce: For recommendation systems, determining a customer's likelihood to purchase a product.
• Fraud Detection: Identifying fraudulent activities in banking and insurance.

Strengths and Limitations

Strengths

• Versatility: Can be used for both classification and regression tasks.
• Handles Large Data Sets: Efficiently processes large databases.
• Automatic Feature Selection: Offers insights into feature importance.

Limitations

• Complexity: More complex and computationally intensive than decision trees.
• Model Interpretability: The model is not as easy to interpret as a single decision tree.
• Overfitting with Noisy Data: While it is resistant to overfitting, random forests can still overfit noisy datasets.

Advanced Topics

• Feature Importance: Random Forests can be used to rank the importance of variables in a regression or classification problem.
• Handling Missing Values: They can handle missing data by surrogate splits in the trees.
• Parallelization: Training of the trees can be easily parallelized, as each tree is built independently.

References

1. Breiman, L. (2001). Random forests. Machine learning, 45(1), 5-32.
2. Liaw, A., & Wiener, M. (2002). Classification and regression by randomForest. R News, 2(3), 18-22.