Linear Discriminant Analysis Classifier

Introduction

Linear Discriminant Analysis (LDA) is widely used in machine learning and statistics for pattern classification and dimensionality reduction. It works by maximizing the ratio of between-class variance to the within-class variance in any particular data set, thereby ensuring maximum separability.

Background and Theory

LDA is based on the concept of searching for a linear combination of variables (features) that best separates two or more classes. This concept can be traced back to Ronald A. Fisher in 1936 with the introduction of Fisher's linear discriminant.

The mathematical foundation of LDA considers two key statistical properties:

• The mean vectors (centroids) of the classes.
• The variance within each class and between the classes.

How the Algorithm Works

Mathematical Formulation

Given a dataset with $d$ dimensions and $N$ samples, suppose we have $C$ classes. Let $\mathbf{x}_i$ be a sample with class label $y_i$. The goal of LDA is to project $\mathbf{x}_i$ onto a lower-dimensional space $S$ that maximizes the class separability.

The within-class scatter matrix $S_W$ and the between-class scatter matrix $S_B$ are defined as follows:

• Within-class scatter matrix $S_W$
  $S_W = \sum_{c=1}^{C} S_{W_c} = \sum_{c=1}^{C} \sum_{\mathbf{x}_i \in \text{class}_c} (\mathbf{x}_i - \mathbf{\mu}_c)(\mathbf{x}_i - \mathbf{\mu}_c)^T$
  where $\mu_c$ is the mean vector of class $c$.
  
• Between-class scatter matrix $S_B$
  $S_B = \sum_{c=1}^{C} N_c (\mathbf{\mu}_c - \mathbf{\mu})(\mathbf{\mu}_c - \mathbf{\mu})^T$
  where $N_c$ is the number of samples in class $c$ and $\mathbf{\mu}$ is the overall mean of the dataset.
  

The objective is to maximize the Fisher criterion, which is defined as the ratio of the determinant of the between-class scatter matrix to the within-class scatter matrix.

where $W$ is the matrix of the projection vectors.

Solving for W

The optimal $W$ can be found by solving the eigenvalue problem:

Implementation

Parameters

No parameters.

Examples

Test with the iris flower dataset:

from luma.classifier.discriminant import LDAClassifier
from luma.preprocessing.scaler import StandardScaler
from luma.model_selection.split import TrainTestSplit
from luma.reduction.linear import PCA
from luma.visual.evaluation import DecisionRegion, ConfusionMatrix

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import numpy as np


X, y = load_iris(return_X_y=True)

X_train, X_test, y_train, y_test = TrainTestSplit(X, y,
                                                  test_size=0.2, 
                                                  random_state=42).get

sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.fit_transform(X_test_std)

lda = LDAClassifier()
lda.fit(X_train_pca, y_train)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

X_trans = np.concatenate((X_train_pca, X_test_pca))
y_trans = np.concatenate((y_train, y_test))

dec = DecisionRegion(lda, X_trans, y_trans)
dec.plot(ax=ax1)

conf = ConfusionMatrix(y_trans, lda.predict(X_trans))
conf.plot(ax=ax2, show=True)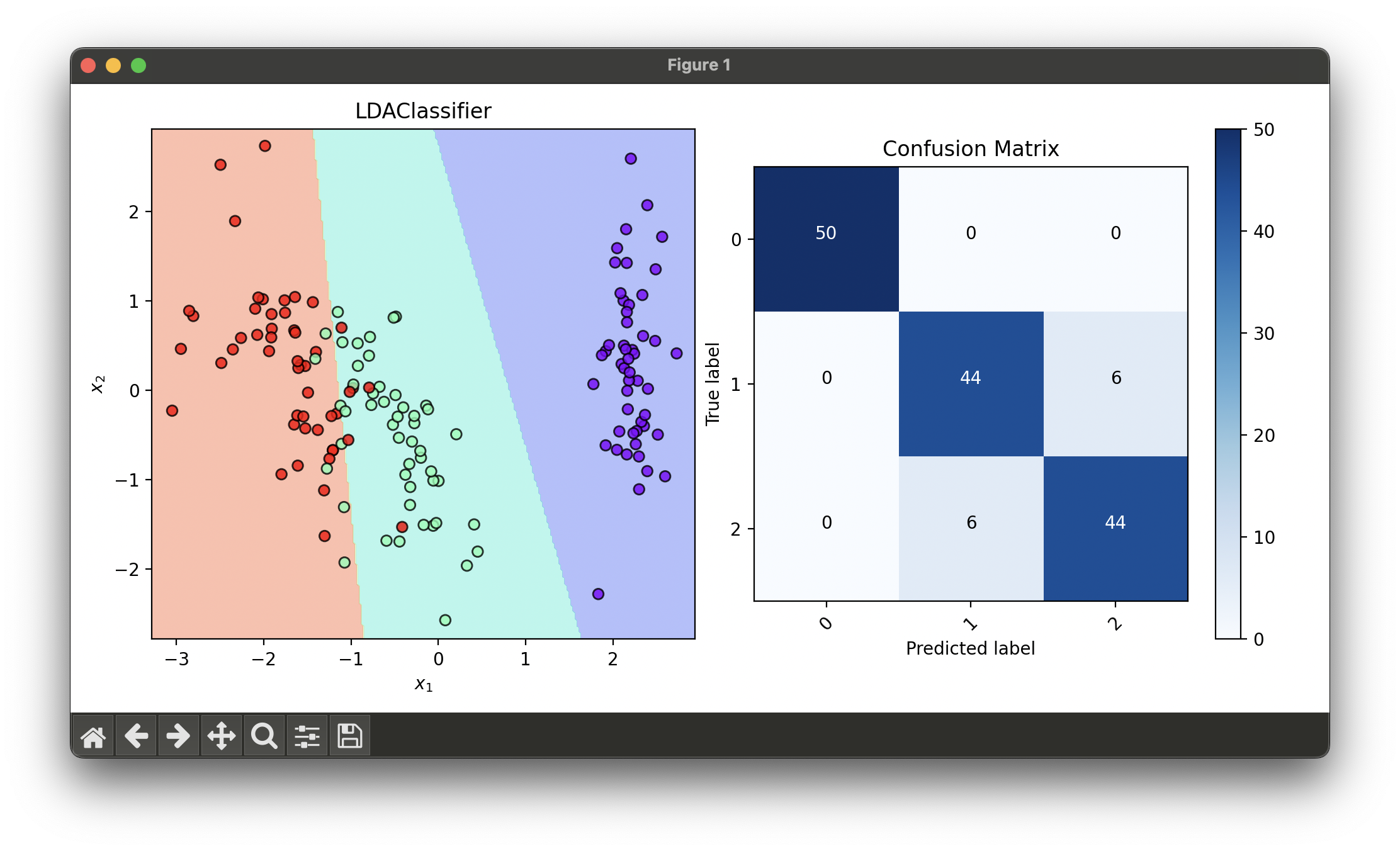

Notes

• To use LDA for dimensionality reduction, refer to luma.reduction.linear.LDA

Application and Use Cases

LDA is used in various fields such as facial recognition, medical diagnosis, and financial fraud detection, where it helps in reducing the number of features while retaining the characteristics that contribute most to the classification.

Strengths and Limitations

• Strengths
  • Reduces computational costs by lowering the dimensionality
  • Minimizes the risk of overfitting
• Limitations
  • Assumes that the data is normally distributed
  • Assumes that the classes have identical covariance matrices
  • Less effective if the mean vectors are not well separated

Advanced Topics and Further Reading

For those interested in exploring beyond basic LDA, topics such as Quadratic Discriminant Analysis (QDA) and Regularized Discriminant Analysis (RDA) offer more flexibility by relaxing some of LDA's assumptions.

References

1. Fisher, Ronald A. "The use of multiple measurements in taxonomic problems." Annals of Eugenics, vol. 7, no. 2, 1936, pp. 179-188.
2. Duda, Richard O., Peter E. Hart, and David G. Stork. Pattern Classification. 2nd ed., Wiley-Interscience, 2001.