ReLU (Rectified Linear Unit) Function

Introduction

The Rectified Linear Unit (ReLU) function is a fundamental activation function used in the field of machine learning, particularly within neural networks. It has gained widespread popularity due to its simplicity and effectiveness in facilitating faster and more efficient training of deep neural networks. The ReLU function is defined mathematically as:

This means that the function outputs the input itself if the input is greater than zero, otherwise, it outputs zero. The simplicity of this function contributes significantly to reducing the computational complexity and mitigating the vanishing gradient problem commonly encountered in deep neural networks.

Background and Theory

Activation functions in neural networks serve to introduce non-linearity into the network, enabling it to learn complex patterns in the data. Prior to the advent of ReLU, sigmoid and hyperbolic tangent (tanh) functions were commonly used. However, these functions are prone to the vanishing gradient problem, where gradients become increasingly small as they propagate back through the network, making it difficult to train deep networks effectively.

The ReLU function addresses this issue by providing a linear response for positive inputs and zero for non-positive inputs, which helps in maintaining the strength of the gradient even in deep networks. This characteristic has been shown to significantly accelerate the convergence of stochastic gradient descent compared to sigmoid and tanh functions.

Procedural Steps

1. Initialization: When designing a neural network, choose ReLU as the activation function for the neurons in one or more layers.
2. Forward Pass:
   • For each input $x$ to a neuron, apply the ReLU function: $f(x) = \max(0, x)$.
   • This will output $x$ itself if $x > 0$, otherwise, it outputs $0$.
3. Backward Pass (During Training):
   • Compute the gradient of the ReLU function with respect to its input. The derivative is $1$ for $x > 0$ and $0$ for $x \leq 0$.
   • Use this gradient in the backpropagation algorithm to update the weights in the network.

Mathematical Formulation

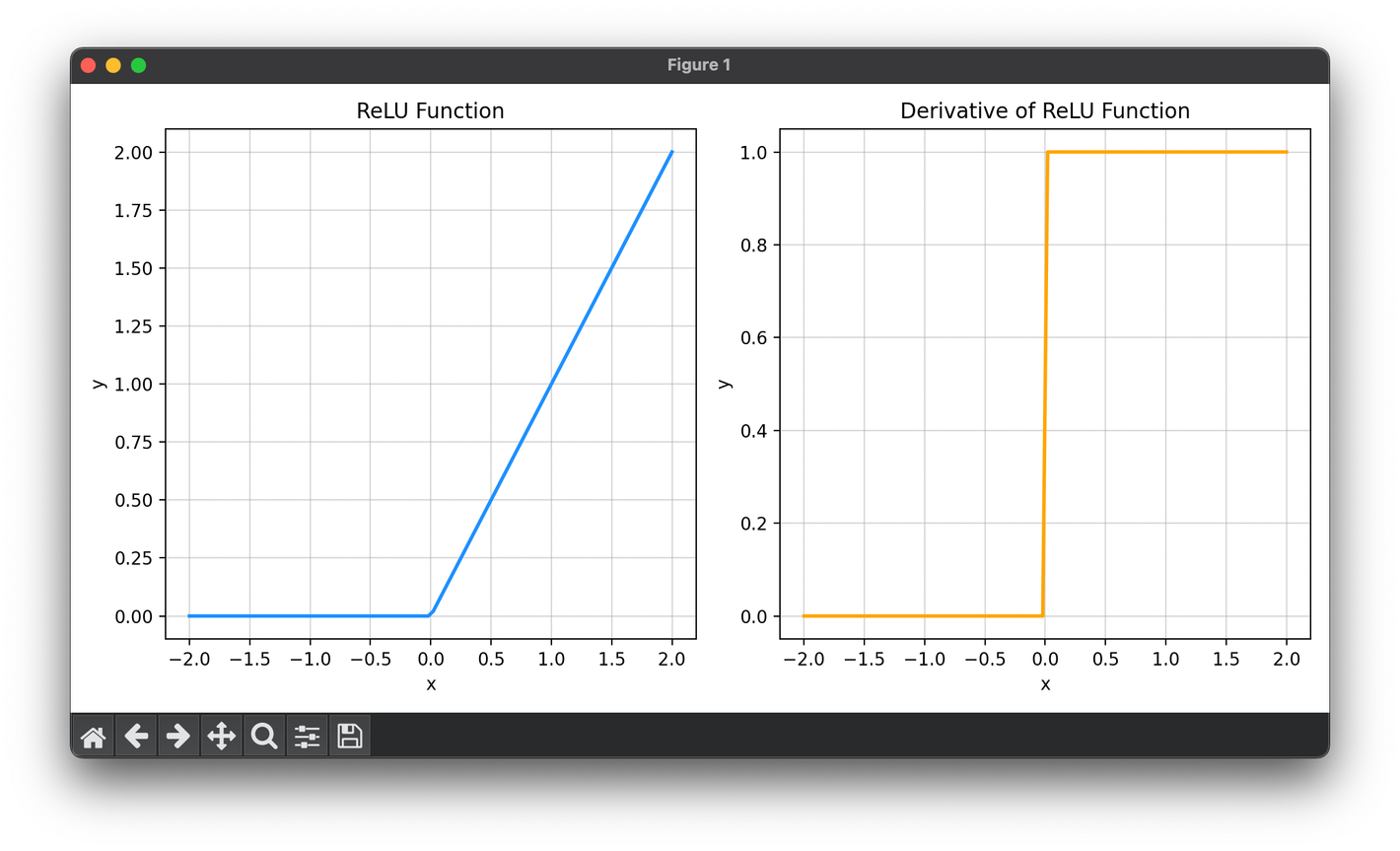
The ReLU function can be mathematically described as:

The derivative of the ReLU function, which is used in the backward pass of network training, is:

Applications

ReLU and its variants are widely used in various types of neural networks, including:

• Convolutional Neural Networks (CNNs): ReLU is extensively used in CNNs for tasks like image classification, object detection, and more.
• Fully Connected Networks: ReLU is a common choice for activation functions in the hidden layers of fully connected networks.
• Autoencoders: ReLU helps in learning compressed representations in autoencoders.
• Deep Reinforcement Learning: ReLU functions facilitate the training of deep neural networks used in reinforcement learning algorithms.

Strengths and Limitations

Strengths:

• Computational Efficiency: ReLU's simple max operation is computationally less expensive than exponential functions like sigmoid or tanh.
• Mitigation of Vanishing Gradient Problem: ReLU helps in maintaining strong gradients during training, which is beneficial for deep networks.

Limitations:

• Dying ReLU Problem: Neurons can become "dead" if they stop outputting anything other than 0. This can occur if a large gradient flowing through a ReLU neuron updates the weights in such a way that the neuron's output is always negative.
• Non-zero Centered Output: ReLU’s output is not zero-centered, which can potentially slow down convergence.

Advanced Topics

Variants of ReLU

Several variants of the ReLU function have been developed to address its limitations, including:

• Leaky ReLU: Introduces a small slope for negative values, preventing neurons from dying.
• Parametric ReLU (PReLU): Allows the slope for negative inputs to be learned during training.
• Exponential Linear Unit (ELU): Reduces the vanishing gradient problem and helps in achieving faster convergence.

Applications in Deep Learning

ReLU and its variants are critical in the success of deep learning models across a wide array of applications, from natural language processing to computer vision, due to their ability to maintain activation over a large range of inputs and facilitate faster training.

References

1. Nair, Vinod, and Geoffrey E. Hinton. "Rectified Linear Units Improve Restricted Boltzmann Machines." Proceedings of the 27th International Conference on Machine Learning (ICML-10). 2010.
2. Maas, Andrew L., et al. "Rectifier Nonlinearities Improve Neural Network Acoustic Models." Proc. ICML. Vol. 30. No. 1. 2013.
3. Clevert, Djork-Arné, Thomas Unterthiner, and Sepp Hochreiter. "Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)." arXiv preprint arXiv:1511.07289 (2015).