Leaky ReLU (Rectified Linear Unit)

Introduction

Leaky Rectified Linear Unit (Leaky ReLU) is an activation function commonly used in deep learning models, particularly in neural networks. It represents an improved version of the basic ReLU (Rectified Linear Unit) function, designed to allow a small, non-zero gradient when the unit is not active and thus not strictly zero. The primary motivation behind the Leaky ReLU is to solve the "dying ReLU" problem, where neurons can sometimes become inactive and cease contributing to the learning process.

Background and Theory

The ReLU Activation Function

ReLU is defined mathematically as:

It outputs the input directly if it is positive; otherwise, it outputs zero. This simplicity leads to fast computation and less vanishing gradient problem compared to sigmoid or tanh functions. However, during the training process, some neurons can permanently output zeros for all inputs, essentially "dying" and contributing nothing to the model's learning.

Introduction to Leaky ReLU

Leaky ReLU aims to address the dying ReLU issue by introducing a small slope $\alpha$ (usually 0.01) for negative input values. Thus, it maintains a gradient for negative values, albeit small. The mathematical representation of Leaky ReLU is:

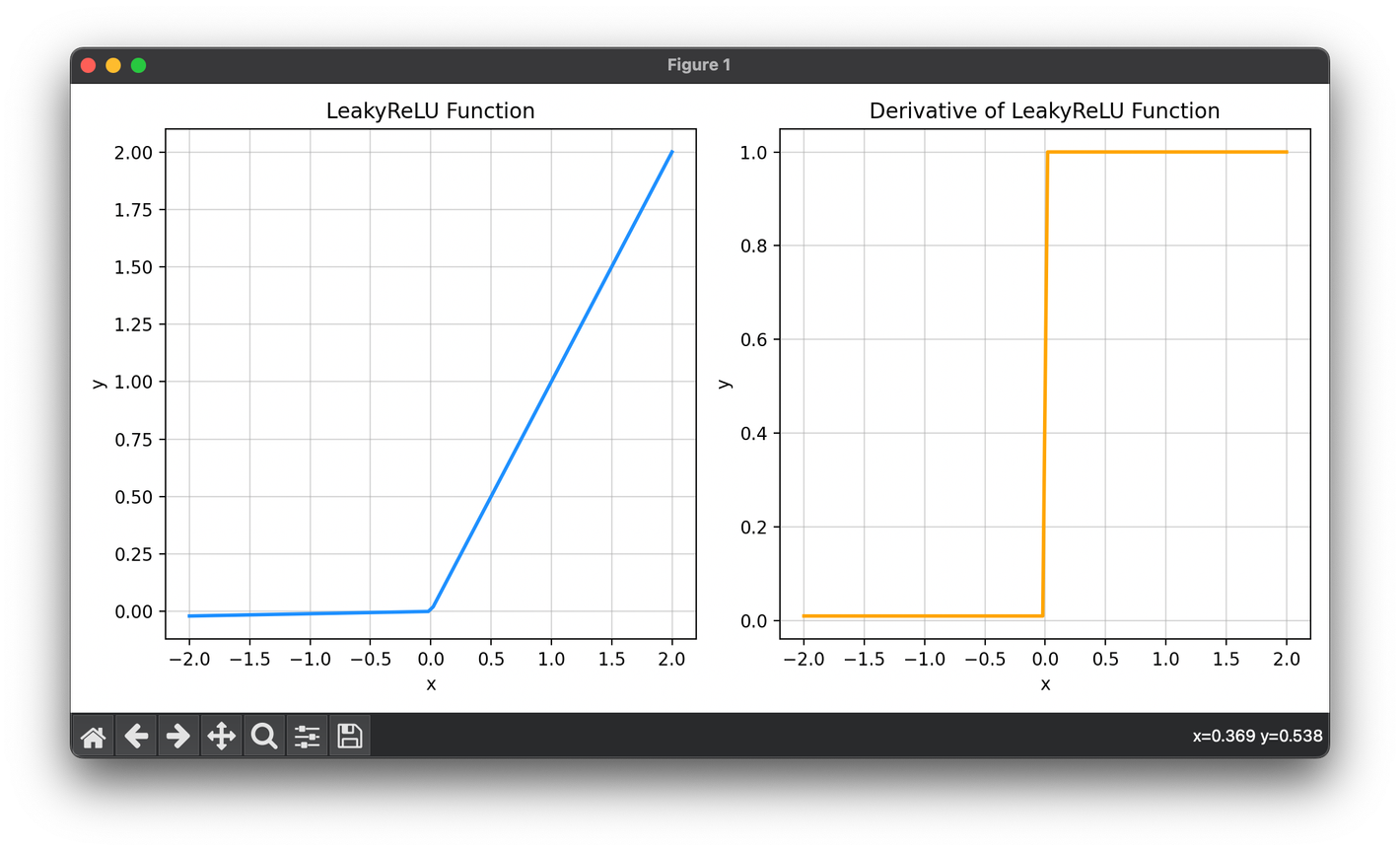
where $\alpha$ is a small constant.

Mathematical Formulation

By allowing a small gradient when $x \leq 0$, Leaky ReLU ensures that all neurons remain "alive" and continue learning. This slight modification can significantly impact the network's ability to converge and learn complex patterns.

For a given input vector $\boldsymbol{x} = [x_1, x_2, \ldots, x_n]$, the Leaky ReLU activation of this vector is calculated element-wise as:

where each $f(x_i)$ is computed using the Leaky ReLU function defined above.

Applications

Leaky ReLU finds applications across a broad spectrum of deep learning models, including:

• Convolutional Neural Networks (CNNs): Used in layers to introduce non-linearity without significantly impacting the computational complexity.
• Fully Connected Networks: Enhances the ability of dense layers to learn complex patterns without the risk of "dying neurons."
• Generative Adversarial Networks (GANs): Helps in stabilizing the training of GANs, where maintaining the flow of gradients is crucial.
• Recurrent Neural Networks (RNNs): Applied in some variations of RNNs to mitigate vanishing gradient issues.

Strengths and Limitations

Strengths

• Mitigates the Dying ReLU Problem: By allowing a small gradient for negative inputs, it keeps all neurons in the network active to some extent.
• Simple and Efficient: Like ReLU, it remains computationally efficient while adding a slight improvement for negative inputs.
• Improves Learning: Has been shown to enhance learning in deep networks by maintaining active participation of more neurons.

Limitations

• Parameter Tuning: The $\alpha$ parameter needs careful tuning, and the optimal value can vary between applications.
• Potential for Unbounded Activation: While rare, the non-zero gradient for negative inputs means that activations can potentially grow large negatively, which might require additional considerations during training.

Advanced Topics

Parametric ReLU (PReLU)

An extension of Leaky ReLU is the Parametric ReLU (PReLU), where $\alpha$ is not a fixed value but a parameter that the model learns during training. This approach allows the network to adaptively learn the most appropriate "leakiness" for each neuron, potentially leading to more flexible and powerful models.

Other Variants

Other variants of ReLU, such as ELU (Exponential Linear Unit) or SELU (Scaled Exponential Linear Unit), offer different takes on handling the negatives and zero-gradient issues, enriching the family of activation functions available for deep learning models.

References

1. Maas, Andrew L., et al. "Rectifier nonlinearities improve neural network acoustic models." Proc. icml. Vol. 30. No. 1. 2013.
2. He, Kaiming, et al. "Delving deep into rectifiers: Surpassing human-level performance on imagenet classification." Proceedings of the IEEE international conference on computer vision. 2015.
3. Clevert, Djork-Arné, Thomas Unterthiner, and Sepp Hochreiter. "Fast and accurate deep network learning by exponential linear units (elus)." arXiv preprint arXiv:1511.07289 (2015).