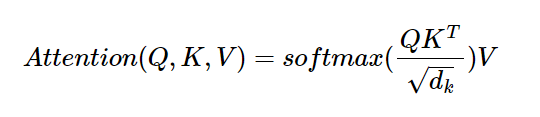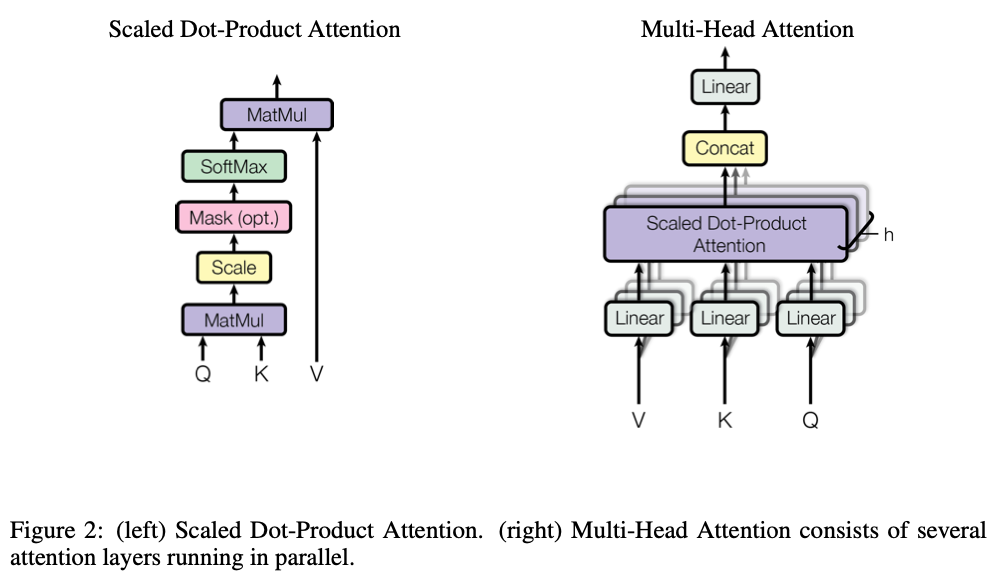
1. 셀프 어텐션 (SDPA(Scaled Dop-Product Attention))

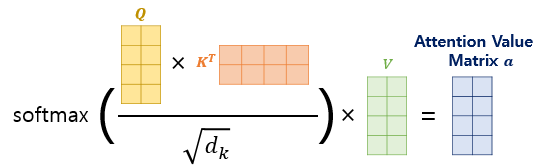
• 수식의 구현 Flow

  • [1] Query벡터와 transpose한 Key벡터의 내적
  • [2] Key벡터의 차원의 루트 값으로 나누어 주어 정규화
  • [3] softmax를 취해주어 도합 1 사이의 확률 벡터로 변환
  • [4] 지금까지 구한 값을 활용해 Value벡터에 가중치 합을 구해줌
    
    

• code

class ScaledDotProductAttention(nn.Module):
    def forward(self,Q,K,V,mask=None):
        d_K = K.size()[-1] # key dimension
        
        scores = Q.matmul(K.transpose(-2, -1)) / np.sqrt(d_K) ## ([1] Query벡터와 transpose한 Key벡터의 내적) / ([2] Key벡터의 차원의 루트 값으로 나누어 주어 정규화)


        if mask is not None: ## option인 Masking 안 했을 경우
            scores = scores.masked_fill(mask==0, -1e9)


        attention = F.softmax(scores,dim=-1) ## ([3] softmax를 취해주어 도합 1 사이의 확률 벡터로 변환)
        out = attention.matmul(V) ## ([4] 지금까지 구한 값을 활용해 Value벡터에 가중치 합을 구해줌)

        return out, attention

• 특징
  • SDPA는 멀티 헤드 어텐션을 support한다.
  • Key 벡터와 Value 벡터의 크기는 같아야 한다.

2. 멀티 헤드 어텐션 (MHA(Multi-Head Attention))

• 특징

  • 멀티헤드의 수로 나눈 크기만큼 배치로 처리가 이뤄진다.
  • dropout 옵션은 논문의 설명에서 포함되어 있지 않지만, 모든 코드에 적용되어 있음
  • 층은 총 4개 (Query/Key/Value 벡터가 곧 하나의 layer + Linear Layer)

    • [1] Query 벡터 층
    • [2] Key 벡터 층
    • [3] Value 벡터 층
    • [4] 연산을 output하기위한 Dense 층

  • 셀프 어텐션과 달리 멀티 어텐션에서는 d_feature를 전체 멀티헤드의 수로 나눈 크기만큼 입력 임베딩 벡터를 split하여 접근
  • 이들로부터 독립적(independent)으로 각 Attention의 matmul을 통한 score 값을 구한 뒤,
  • 멀티헤드 수만큼 구한 각 셀프 어텐션 결과를 다시 d_feature 크기로 concat 해준 것이 최종 결과물 !
  
  

• code

class MultiHeadAttention(nn.Module):
    def __init__(self, d_feat=128, n_head=5, actv=F.relu, USE_BIAS=True, dropout_p=0.1, device=None):
        """
        :param d_feat: feature dimension
        :param n_head: number of heads
        :param actv: activation after each linear layer
        :param USE_BIAS: whether to use bias
        :param dropout_p: dropout rate
        :device: which device to use (e.g., cuda:0)
        """

        super(MultiHeadAttention,self).__init__()

        if (d_feat%n_head) != 0: ## feature dimension이 멀티헤드의 수로 나누어지지 않을 경우 에러 던지기
            raise ValueError("d_feat(%d) should be divisible by b_head(%d)"%(d_feat,n_head)) 


        self.d_feat = d_feat
        self.n_head = n_head
        self.d_head = self.d_feat // self.n_head ## 멀티헤드의 수로 나눈 크기만큼 배치 처리
        self.actv = actv
        self.USE_BIAS = USE_BIAS
        self.dropout_p = dropout_p # prob. of zeroed ## dropout 옵션은 논문의 설명에서 포함되어 있지 않지만, 모든 코드에는 적용되어 있음

        self.lin_Q = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS) ## [1] Query 벡터 층
        self.lin_K = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS) ## [2] Key 벡터 층
        self.lin_V = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS) ## [3] Value 벡터 층
        self.lin_O = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS) ## [4] 연산을 output하기위한 Dense 층

        self.dropout = nn.Dropout(p=self.dropout_p) ## Drop-out 설정
    


    def forward(self,Q,K,V,mask=None):
        """
        :param Q: [n_batch, n_Q, d_feat]
        :param K: [n_batch, n_K, d_feat]
        :param V: [n_batch, n_V, d_feat] <= n_K and n_V must be the same 
        :param mask: 
        """

        n_batch = Q.shape[0]
        Q_feat = self.lin_Q(Q) 
        K_feat = self.lin_K(K) 
        V_feat = self.lin_V(V)
        # Q_feat: [n_batch, n_Q, d_feat]
        # K_feat: [n_batch, n_K, d_feat]
        # V_feat: [n_batch, n_V, d_feat]


        # Multi-head split of Q, K, and V (d_feat = n_head*d_head)
        Q_split = Q_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
        K_split = K_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
        V_split = V_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
        # Q_split: [n_batch, n_head, n_Q, d_head]
        # K_split: [n_batch, n_head, n_K, d_head]
        # V_split: [n_batch, n_head, n_V, d_head]

        # Multi-Head Attention
        d_K = K.size()[-1] # key dimension
        
        scores = torch.matmul(Q_split, K_split.permute(0, 1, 3, 2)) / np.sqrt(d_K)
        ## 셀프 어텐션과 달리 멀티 어텐션에서는 d_feature를 전체 멀티헤드의 수로 나눈 크기만큼 입력 임베딩 벡터를 split하여 접근
        ## 이들로부터 독립적(independent)으로 각 Attention의 matmul을 통한 score 값을 구한 뒤,
        ## 멀티헤드 수만큼 구한 각 셀프 어텐션 결과를 다시 d_feature 크기로 concat 해준 것이 최종 결과물 !





        if mask is not None:
            scores = scores.masked_fill(mask==0,-1e9)


        attention = torch.softmax(scores,dim=-1)
        x_raw = torch.matmul(self.dropout(attention), V_split) # dropout is NOT mentioned in the paper
        # attention: [n_batch, n_head, n_Q, n_K]
        # x_raw: [n_batch, n_head, n_Q, d_head]



        # Reshape x
        x_rsh1 = x_raw.permute(0,2,1,3).contiguous()  ## (torch.permute()함수로 차원에 순서를 주어 모든 차원을 서로 맞교환(?) 해줌과 동시에 contiguous()함수를 불러주어, contiguous tensor로 안전하게 설정해줌)
        # x_rsh1: [n_batch, n_Q, n_head, d_head]

        x_rsh2 = x_rsh1.view(n_batch,-1,self.d_feat) ## 다시 원래 차원인 d_featur로 view()함수를 통해 차원을 축소시켜 줌.
        # x_rsh2: [n_batch, n_Q, d_feat]



        # Linear
        x = self.lin_O(x_rsh2)
        # x: [n_batch, n_Q, d_feat]

        out = {'Q_feat':Q_feat,'K_feat':K_feat,'V_feat':V_feat,
               'Q_split':Q_split,'K_split':K_split,'V_split':V_split,
               'scores':scores,'attention':attention,
               'x_raw':x_raw,'x_rsh1':x_rsh1,'x_rsh2':x_rsh2,'x':x}
        return out

❓

torch.transpose(input, int dim0, int dim1)

• Key벡터와 transpose된 Key벡터를 출력해본 결과
  

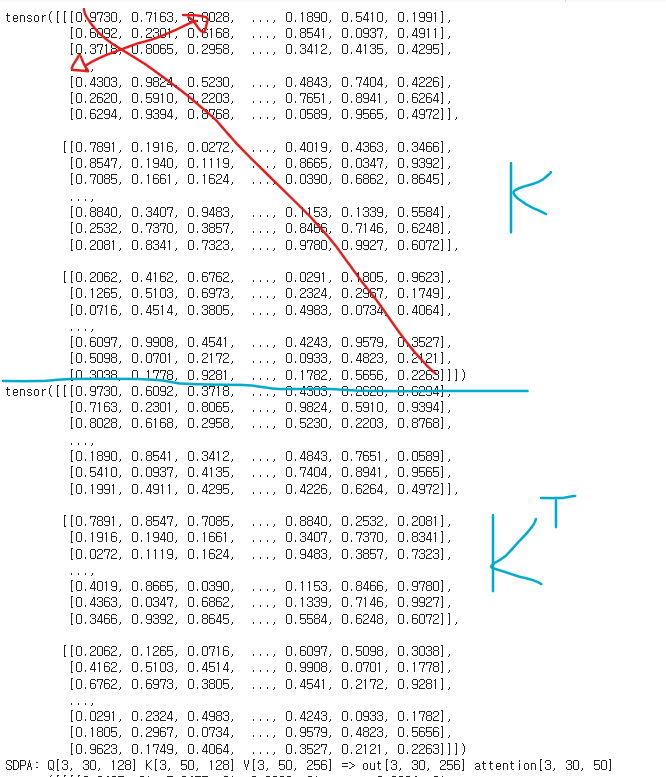
torch.matmul()

• 두 텐서 간의 Matrix product(행렬 곱)
• 두 텐서의 차원의 크기(dimension)에 따라 적용되는 연산이 달라지는데,

  • [5] 두 tensor 모두 1 dimensional이상이고 하나의 tensor가 3이상의 N dimensional이면, batched matrix multiply가 수행된다. 첫번째 tensor가 1 dimensional이면 1차원이 앞에 추가되어 batched matrix multipy를 수행하고, 수행후에 추가된 dimension은 사라진다. non-matrix dimension (batch)는 broadcast된다. 예를 들면 첫번째 tensor가 (j x 1 x n x n) tensor이고, 두번째 tensor가 (k x n x n) tensor일 때, output은 (j x k x n x n) tensor가 된다. broad casting logic은 input이 broadcast 가능할 때에 batch dimension에만 해당된다. 예를 들면 첫번째 tensor가 (j x 1 x n x m) tensor이고, 두번째 tensor가 (k x m x p) tensor일 때 matrix dimension이 달라도 broadcasting이 유효하다. output은 (j x k x n x p) tensor가 된다.
    (참고: https://velog.io/@optjyy/torch.matmul)

📝 회고

• 🙋‍ [1]Query 벡터와 transpose한 Key 벡터 간의 "내적" & [2]softmax 함수를 취한 일종의 가중치와 Value 벡터 간의 "가중치 합(Weighted Sum)"
  ➡️ 둘다 구현코드에서는 동일하게 torch.matmul() 사용 ❓
  • Attention 매커니즘의 이론을 설명할 때에는 "내적"과 "가중치 합" 이라고 표현하지만, 계산은 동일하게 matmul 함수를 통해 이뤄질 수 있는 것 같다.

• 💡 Attention 매커니즘에서 각 Query 벡터/Key 벡터/Value 벡터 , 그리고 결과로 출력되는 Attention Value(어텐션 값) 행렬의 크기에 대한 고찰

  • 

  
  

  • 

  • 각 time-step의 i번째 요소에 대해 representation(재현성 개념?)을 계산한 결과 Attention Value(어텐션 값)는 스칼라 값이 아니라 벡터(리스트)이다..! ✨
  • 그리고 전체 Attention Value(어텐션 값) 행렬은 이들이 합쳐진 Matrix다..! ✨

기타 참고

• 코드 구현 시 사용되는 PyTorch 함수들이 잘 정리된 글 참고 ✨

  • [[PyTorch] view, reshape, transpose, permute함수의 차이와 contiguous] https://sanghyu.tistory.com/3
    
    

• 위키독스

  • https://wikidocs.net/31379

• Query 벡터/Key 벡터/Value 벡터 행렬 계산해본 예제
  • https://ratsgo.github.io/nlpbook/docs/language_model/tr_self_attention/