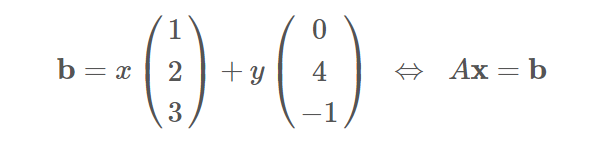벡터공간(vector space)
참고: https://gaussian37.github.io/math-la-linekej_12/
다음 조건을 만족하는 벡터 집합 V를 벡터공간(Vector Space)라고 정의한다.
하지만 다음 10가지 조건 중, 3가지 조건을 통해 벡터공간인지 아닌지를 빠르게 판별할 수 있다.
문제 1.
답 : (2)
v1, v2, v3가 집합을 이루는 각각의 원소일때, zero vector가 존재하는지부터 확인한다.
(1) v1+v2 = 0.
v1, v2, v3 = (0,0,0), (1,-1,0), (3,-3,0) ...
1) zero : (0,0,0)
2) v+w < V
(1,-1,0) + (3,-3,0) = (4,-4,0), (4,-4,0)는 v1+v2 = 0이므로, 집합 V에 속한다.
3) kv < V
2(1,-1,0) = (2,-2,0), (2,-2,0)는 v1+v2 = 0이므로, 집합 V에 속한다.
(2) v1+v2+v3 = 1
1) zero: (0,0,0), (0,0,0)은 v1+v2+v3 = 1을 만족하지 않으므로 벡터공간이 아님.
(3) 2v2 = v3, v1+v3 = 0
1) zero: (0,0,0), 위의 식 만족.
2) v+w < V, (0,0,0), (-2,1,2)일때, 위의 식을 만족하면서 조건2 만족.
3) kv < V, 2(-2,1,2) = (-4,2,4)일때, 위의 식을 만족하면서 조건3 만족.
(4) v1 = 2v2 = 3v3
1) zero: (0,0,0), 위의 식 만족.
2) v+w < V, (0,0,0), (6,3,2)일때, 위의 식을 만족하면서 조건2 만족.
3) kv < V, 2(6,3,2) = (12,6,4)일때, 위의 식을 만족하면서 조건3 만족.
부분공간 (Subspace)
& V(전체공간)의 부분공간에는 반드시 {0}과 자기 자신 V가 존재한다.
-> 부분공간의 조건(벡터공간의 조건)을 만족하기 때문에.
문제 2.
(1) a,b를 지나는 직선
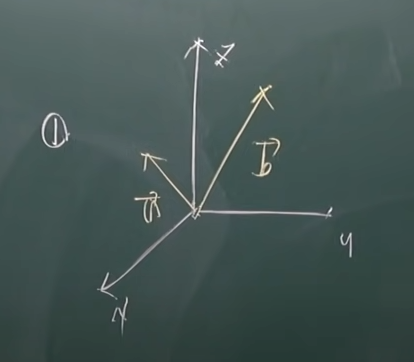
원점(0,0,0)을 지나지 않음 = 벡터공간의 조건을 만족하지 않으므로 부분공간 아님.
(2) a,b,c를 지나는 직선
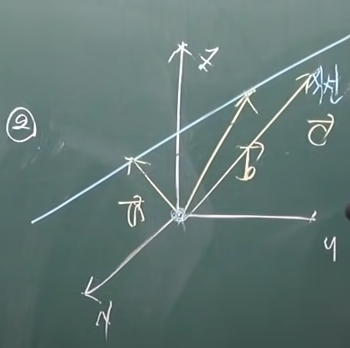
원점(0,0,0)을 지나지 않음 = 벡터공간의 조건을 만족하지 않으므로 부분공간 아님.
(3) a,b,c에 모두 직교하는 벡터들의 집합
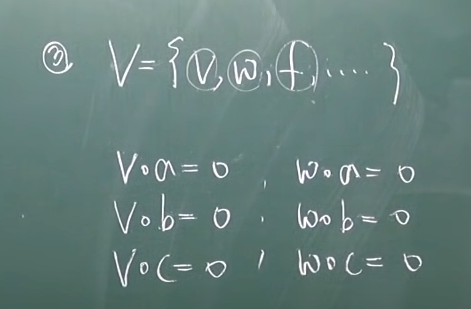
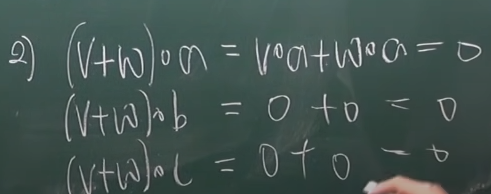
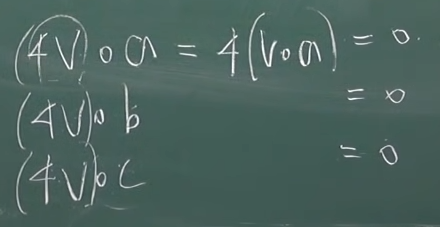
(4) {x<R**3 : (a.x, b.x, c.x) = (0,0,-1)} (a.x = 내적기호)
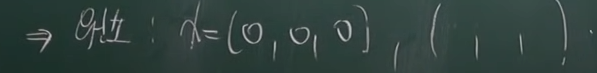
(0,0,0)이 존재할 수 없음 = 벡터공간의 조건을 만족하지 않으므로 부분공간 아님.
문제 3.
답: ㄹ
ㄱ. 직선이 없으므로
ㄴ. 직선이 없으므로
ㄷ. 원점을 지나는 직선이 없으므로
또한, R3의 부분공간은 {0}, {R3}, 원점을 지나가는 직선 뿐이다
-> 틀림.
원점을 지나가는 평면도 포함될 수 있음.
2. 공간
2-1. 열공간(Column space) & 행공간 (Row space)
행벡터(row vector)와 열벡터(column vector)
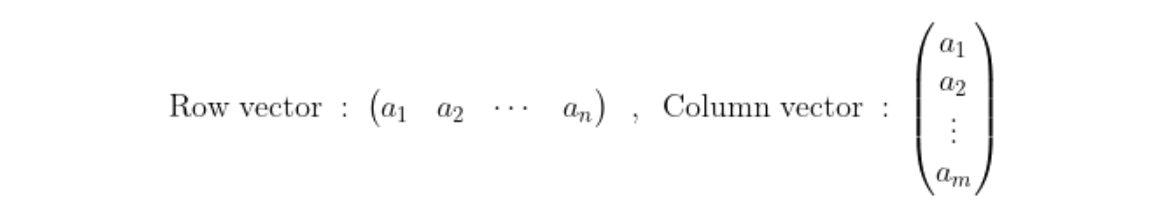
행공간이란?
에 대하여, A의 m개 행들
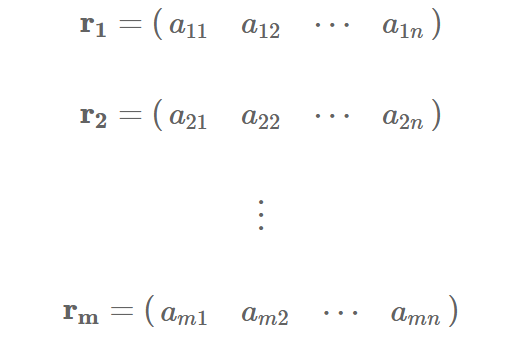
의 선형결합으로 생성(span)된 부분공간 R(A) = {r1, r2, ... , rm}를 행렬 A의 '행공간(Row Space)'이라 부른다.
열공간이란?
A의 n개의 열들
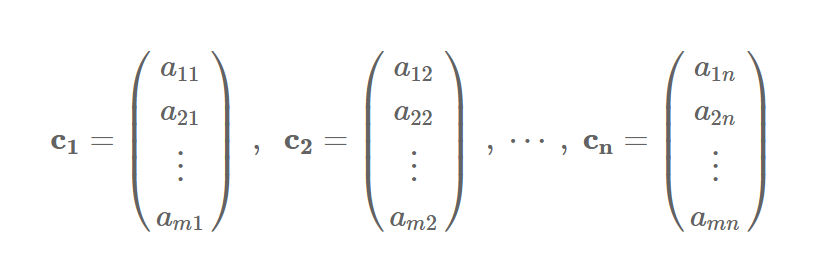
의 선형결합으로 생성(span)된 부분공간 C(A) = {c1, c2, ... , cn}을 행렬 A의 '열공간(Column space)'이라 부른다.
2-2. 영공간(Nullspace)
방정식 Ax = 0의 해집합으로, 모든 해를 포함하며, N(A)로 표기한다. 이 해집합의 벡터들 x는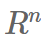 
에 속한다.
열공간과 비교하였을 때, 영공간 N(A)는 Rn의 부분공간이고,
열공간 C(A)는 Rm의 부분공간이다.
[행렬의 영공간을 구하고 동차방정식 푸는 법]
Rank of matrix (행렬의 랭크)
행공간과 열공간의 차원은 행렬의 랭크와 같다.
임의의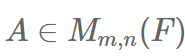 
에 대하여 행렬 A의 랭크(rank)는 A의 행랭크(=열랭크)로 정의되고, 다음이 항상 성립한다.
[Rank(랭크)의 정의]
랭크에 대한 정의는 크게 4가지로 분류할 수 있다.
2개는 Linear transform(선형변환)과 관련된 정의이고, 나머지 2개는 matrix(행렬)와 관련된 것이다.
행렬에 관한 정의
행렬 A의 랭크는 rank(A)로 표기하고 다음이 가르키는 것과 같다.
1. 행렬의 일차독립인 행 또는 열의 최대 개수
Ex) m x n 행렬에서 m개의 행과 n개의 열이 있다.
모든 열이 서로 일차독립이라면, 행렬의 랭크는 n, 모든 행이 서로 일차독립이라면 행렬의 랭크는 m이 된다.
단 모든 행끼리, 모든 열끼리 서로 일차독립인 경우는 없다
전문적인 말로는 '한 행렬의 열공간의 차원과 행공간의 차원은 같다'
2. 행렬 A의 pivots의 개수
Ex)
피벗설명글 참고
3. 그 행렬의 열벡터들에 의해 생성된 벡터공간의 차원(dimension).
연립방정식 Ax = b의 해가 존재한다 <=> 벡터 b는 열 A의 열공간(Column space)의 원소이다.
연립방정식이 다음과 같이 주어져있을 때,이것을 만족하는 해 b는 어떻게 구할까(어떻게 표현할 수 있는가?)
=> 행렬 곱의 선형결합적 관점에서 바라보면 b는 행렬 A의 열벡터들이 만들어내는 벡터공간의 원소가 되어야 한다.
즉,이는 b가 A의 열공간에 포함되어 있어야 한다는 것을 의미한다.
