Scalar (스칼라)
- 정의 : 크기만을 나타내는 물리량.
크기와 방향 모두 나타내는 물리량인 벡터와 반대되는 개념.
Ex) x = 2
Vector (벡터)
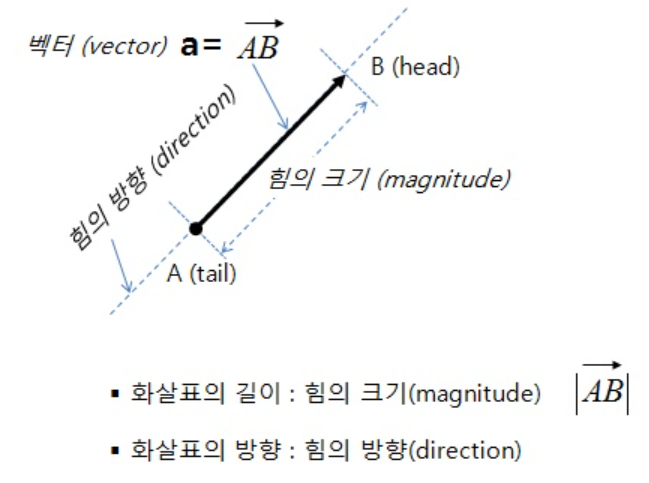
- 정의 : 크기와 방향 모두 나타내는 물리량.
(벡터 AP = 시점 A에서 종점 P로 가는 유향성분 AP.) - 특징:
- scalar(스칼라)의 집합, matrix(행렬)을 구성하는 기본 단위
- 알파벳 두개로 시작점과 끝점을 나타내지만,
일반적으로 A벡터, B벡터라고 일컬어지는 벡터들은 원점 O에서 시작함.
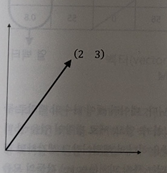
Ex) 2차원 벡터
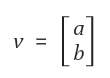
=> a, b = 벡터의 성분(component), v= 벡터.
=> 위에서 정의한 벡터 v는 2차원에서 정의된 벡터, 정확히 말하면 2차원의 Column Space에 존재하는 벡터.
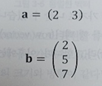
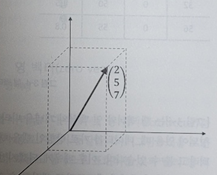
Ex) 3차원 벡터
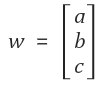
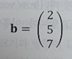
벡터의 종류
1. 영벡터
정의: 크기가 0인 벡터.
어떤 벡터에 더해져도 원래 벡터 그대로가 되게 하는 벡터 = 벡터공간에서의 덧셈에 대한 '항등원'이 되는 벡터.

2. 헹벡터
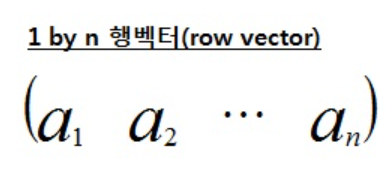
3. 열벡터

4. 단위벡터
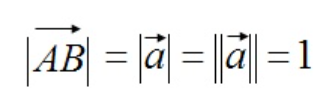
벡터의 연산
다음과 같은 벡터 v, w가 있을 때,
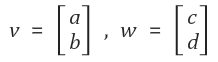
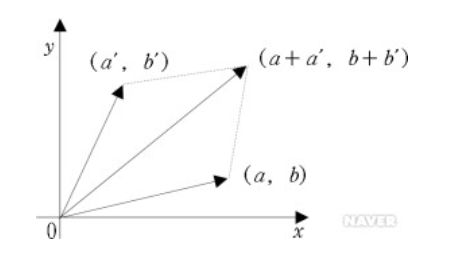
1. 벡터의 합
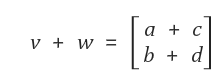
2. 벡터의 스칼라곱
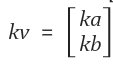
3. 벡터의 내적
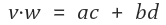
Matrix (행렬)
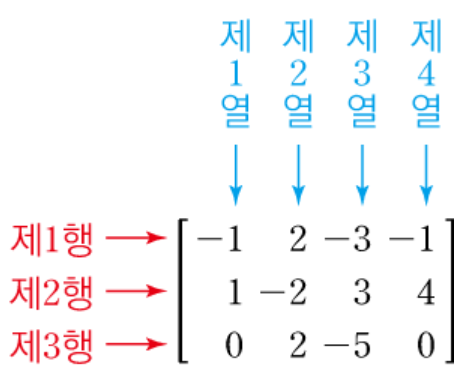
- 정의: 수 또는 변수 등의 일련의 개체들을 행(Row)과 열(Column)에 맞추어 직사각형 모양으로 순서 있게 배 열하여 괄호[ ]로 묶은 것.
행렬의 연산
1. 행렬의 덧셈과 뺄셈
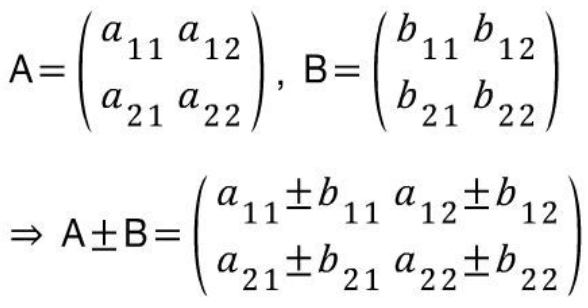
2. 행렬의 곱셈-스칼라곱셈
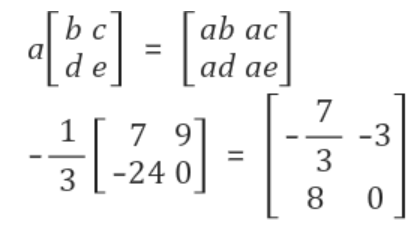
2. 행렬의 곱셈-행렬의 곱셈
- 조건 : 앞행렬의 열의 개수와 뒤행렬의 행의 개수가 같아야 함.
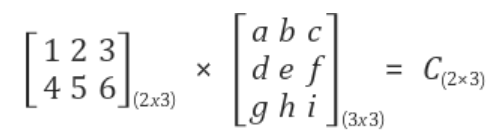
행렬 연산의 성질

다양한 행렬
1. 전치 행렬 (transposed matrix)
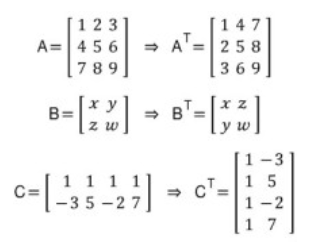
- 정의 : 기존 행렬의 행과 열을 바꾼 행렬
- 성질:
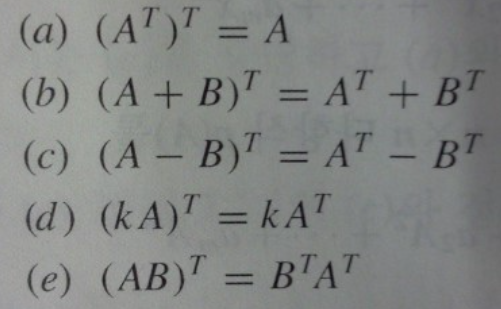
2. 대칭행렬
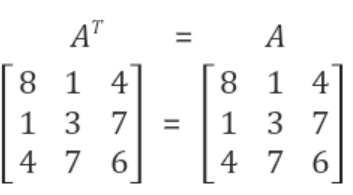
- 정의: 기존 행렬과 전치 행렬이 동일한 정사각 행렬.
- 성질: 대칭행렬의 덧셈, 뺄셈, 제곱도 모두 대칭행렬이 됨.
3. 대각행렬

- 정의 : 행렬의 주 대각 원소가 아닌 원소가 0인 정사각 행렬.
- 성질 : 대각행렬과 어떤 행렬을 곱했을 때, 대각 행렬을 왼쪽에 위치시키면 어떤 행렬의 행이 대각 원소의 배수만큼 변환됨.
4. 단위행렬
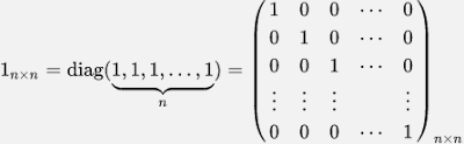
- 정의: 주 대각 원소가 1이고 그 밖의 나머지 원소는 모두 0인 대각 행렬.
- 특징 : 단위행렬에 어떤 행렬을 곱해도 그 어떤 행렬과 동일함.
5. 삼각행렬
정의: 행렬의 구성 원소가 삼각형 형태를 띠는 행렬.
성질: 삼각 행렬 간 덧셈, 뺄셈, 행렬 곱의 결과는 모두 삼각 행렬임.
5-1. 상 삼각행렬
5-2. 하 삼각행렬

6. 토플리츠 행렬
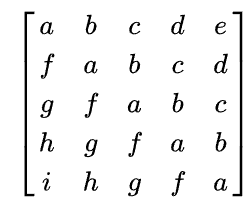
선형대수학에서 오토 토플리츠의 이름을 딴 토우플리츠 행렬이나 대각선 정수 행렬은 각각 왼쪽에서 오른쪽으로 대각선으로 내려가는 행렬이 일정함.