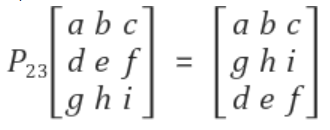1. 단위행렬(Identity Matrix)
행렬의 주대각 원소(Diagonal Component)가 모두 1이고, 나머지 원소는 모두 0인 대각행렬
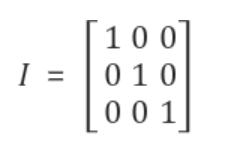
1-1. 단위 행렬의 성질
행렬 곱 위치와 상관없이 기존 행렬에 단위 행렬은 곱한 결과는 기존 행렬과 동일하다.
AI = IA = A
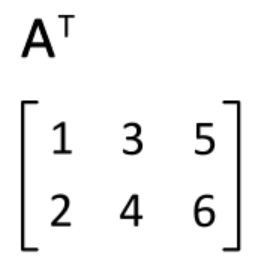
2. 전치 행렬(transposed matrix)
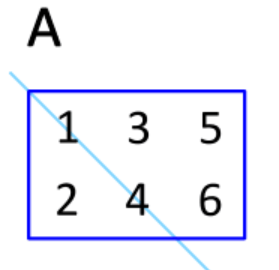
행과 열을 교환하여 얻는 행렬
1.
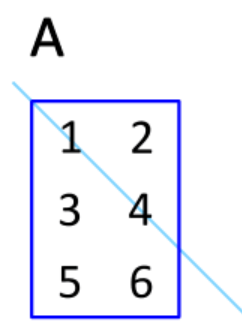
2. 주대각선을 축으로 반사 대칭
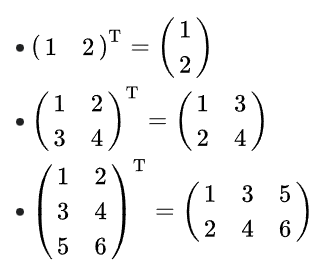
3. 대칭 행렬(Symmetric matrix)
전치 행렬이 스스로와 같은 행렬
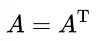
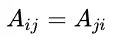
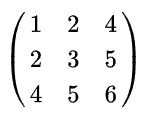
3-1. 대칭 행렬의 성질
3-1-1. 대칭 행렬 간 덧셈이나 뺄셈의 결과 또한 대칭 행렬이다. (곱셈은 x)
3-1-2. 대칭 행렬의 거듭 제곱 또한 대칭 행렬이다.
3-1-3. 행렬 A에 대해 ATA와 AAT의 결과는 대칭행렬이다.
4. 대각행렬(diagonal matrix)
주대각선 성분이 아닌 모든 성분이 0인 정사각 행렬

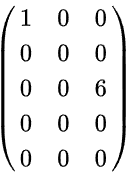

4-1. 대각행렬 예시
단위행렬, 영행렬, 스칼라행렬(단위행렬의 배수 행렬로 주대각 성분의 모든 원소의 값이 같다.)
4-2. 대각행렬의 성질
어떤 행렬에 대각 행렬을 곱할 때,
대각 행렬을 "오른쪽"에 곱하는 경우, "기존 행렬의 열 값"이 대각 원소의 배수가 되며, 대각 행렬을 "왼쪽"에 곱하는 경우 "기존 행렬의 행 값"이 대각 원소의 배수가 된다.
5. 삼각 행렬(triangular matrix)
6. 토플리츠 행렬(Toeplitz matrix)
왼쪽에서 오른쪽으로 내려가는 각 대각선이 일정한 행렬

7. 역행렬(Inverse Matrix)
A가 n x n 이고, 가역행렬이면 A-1 = 1/det(A) * adj(A)
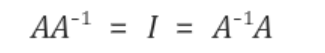
이때 A-1은 1/A가 아님.
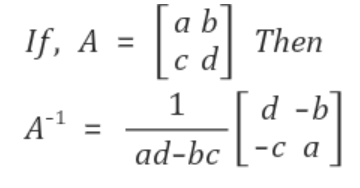
-> 추후 역행렬 변환에 관한 목차에서 더 자세히 다룰 예정
치환행렬(Permutation Matrix)
기존 행렬의 행의 순서를 교체(치환)해주는 행렬
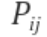
-> i번째 행과 j번째 행의 순서를 바꿈을 의미함.
치환행렬은 단위행렬(Identity Matrix)의 순서를 바꿈으로써 정의할 수 있고, 3차 정방행렬(3 by 3 Matrix)에서 치환행렬 은 아래와 같이 정의됨.
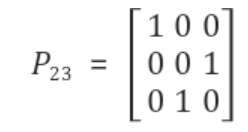
실제로, 행렬에 치환행렬을 곱해보면 행의 순서가 바뀌는 것을 알 수 있음.