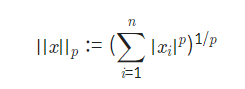정규화(Regularization)란?
정칙화라고 불리며 과적합을 해결하기 위한 방법(L1, L2 Regularization, Dropout, Batch normalization) 중의 하나이다.
과적합이란 훈련 데이터는 높은 정확도를 보여주지만 검증 데이터나 시험 데이터에서는 그렇지 못한 현상을 말한다.
그래서 정규화 기법들은 모델이 훈련 데이터의 정답을 맞히지 못하도록 과적합을 방해(Train Loss가 증가)하는 역할을 한다. 그로인해 Train Loss는 소폭 증가하지만 최종적으로 Validation Loss나 Test Loss를 감소시킨다.
💡Tip 정규화(Normalization)
한국어로 번역될 때 Regularization과 Normalization 모두 정규화로 번역되어 혼동이 있을 수 있는데 Normalization은 데이터의 형태를 좀 더 의미있게 혹은 훈련에 적합하게 전처리하는 과정을 말한다.
(데이터를 Z-score로 변경하거나 minmax scaler를 사용하여 0과 1사이의 값으로 분포를 조정하는 것들이 해당됨)
결과적으로 Feature의 범위 분포를 동일하게 하여 모델이 풀어야 하는 문제를 좀 더 간다한게 바꾸어 주는 전처리 과정이다.
정리하자면 Regularization은 과적합을 막는 방법이고 Normalization은 훈련시 서로 범위가 다른 데이터들을 같은 범위로 바꿔주는 전처리 과정이다.
Normalization 예제 코드
from sklearn.datasets import load_iris import pandas as pd import matplotlib.pyplot as plt iris = load_iris() iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names) target_df = pd.DataFrame(data=iris.target, columns=['species']) # 0, 1, 2로 되어있는 target 데이터를 # 알아보기 쉽게 'setosa', 'versicolor', 'virginica'로 바꿉니다 def converter(species): if species == 0: return 'setosa' elif species == 1: return 'versicolor' else: return 'virginica' target_df['species'] = target_df['species'].apply(converter) iris_df = pd.concat([iris_df, target_df], axis=1) iris_df.head()
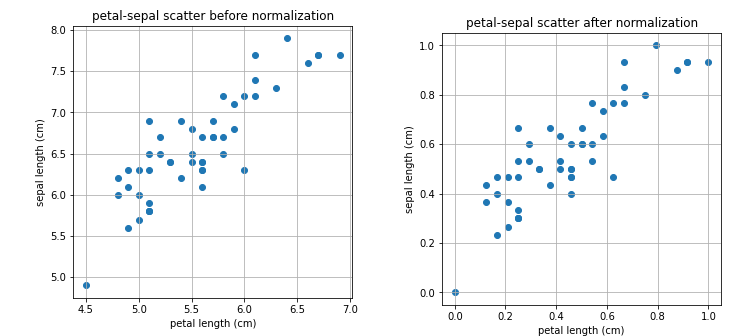
💡Tip X축과 Y축을 확인해 보자!
📄Output
Regularization 예제 코드
from sklearn.linear_model import LinearRegression import numpy as np X = np.array(X) Y = np.array(Y) # Iris Dataset을 Linear Regression으로 학습합니다. linear= LinearRegression() linear.fit(X.reshape(-1,1), Y) # Linear Regression의 기울기와 절편을 확인합니다. a, b=linear.coef_, linear.intercept_ print("기울기 : %0.2f, 절편 : %0.2f" %(a,b)) plt.figure(figsize=(5,5)) plt.scatter(X,Y) plt.plot(X,linear.predict(X.reshape(-1,1)),'-b') plt.title('petal-sepal scatter with linear regression') plt.xlabel('petal length (cm)') plt.ylabel('sepal length (cm)') plt.grid() plt.show() #L1 regularization은 Lasso로 import 합니다. from sklearn.linear_model import Lasso L1 = Lasso() L1.fit(X.reshape(-1,1), Y) a, b=L1.coef_, L1.intercept_ print("기울기 : %0.2f, 절편 : %0.2f" %(a,b)) plt.figure(figsize=(5,5)) plt.scatter(X,Y) plt.plot(X,L1.predict(X.reshape(-1,1)),'-b') plt.title('petal-sepal scatter with L1 regularization(Lasso)') plt.xlabel('petal length (cm)') plt.ylabel('sepal length (cm)') plt.grid() plt.show() #L2 regularization은 Ridge로 import 합니다. from sklearn.linear_model import Ridge L2 = Ridge() L2.fit(X.reshape(-1,1), Y) a, b = L2.coef_, L2.intercept_ print("기울기 : %0.2f, 절편 : %0.2f" %(a,b)) plt.figure(figsize=(5,5)) plt.scatter(X,Y) plt.plot(X,L2.predict(X.reshape(-1,1)),'-b') plt.title('petal-sepal scatter with L2 regularization(Ridge)') plt.xlabel('petal length (cm)') plt.ylabel('sepal length (cm)') plt.grid() plt.show()
📄Output
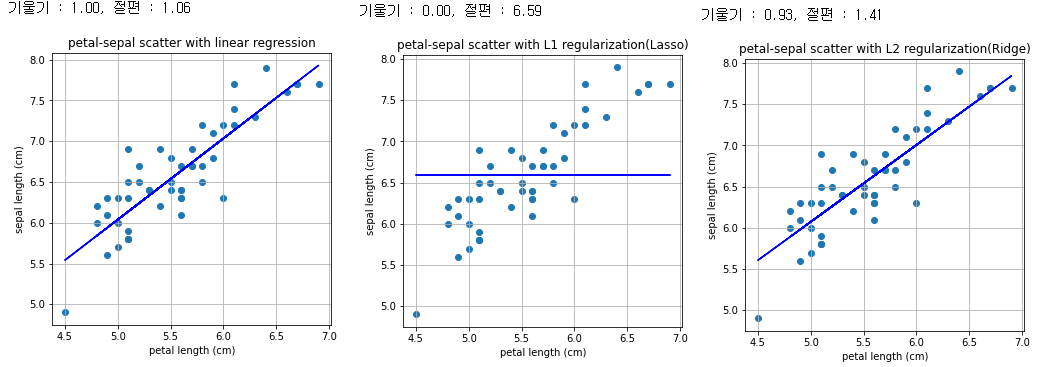
보이는 것과 같이 L1 Regularization은 문제를 풀어내지 못하는 모습을 보이며 L2 Regularization은 제대로된 결과를 나타내는 것으로 보아 Linear Regression이 L2 Regularization과 관련이 있다는 것을 알 수 있다.
1. L1 Regularization
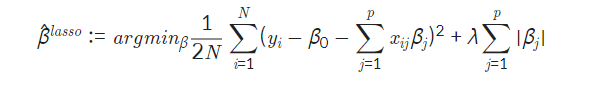
L1 Regularization은 위와 같은 식으로 정의되며 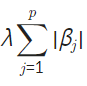
이 부분이 중요한 부분으로 작용한다.
위와 같은 식이 없다면 L1이 아닌 평범한 Linear Regression과 동일하게 되며 이는 L1이라는 이름이 붙은 이유와 L2와의 차이를 나타내는 식이다.
💡Tip Lp Norm
norm은 벡터나 행렬, 함수 등의 거리를 나타낸다.
L1은 norm식에서 p = 1인 경우이기 때문에 L1 Norm이라고 불린다. 또한 사이킷런이나 케라스, 텐서플로우 등의 패키지에서는 Lasso라는 이름으로 더 자주 사용된다.
2. L2 Regularization
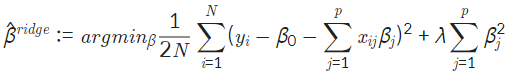
L2 Regularization은 위와 같은 식으로 정의 되며
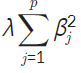
L1과 같이 이 부분이 중요하게 작용하며 다른 점은 p = 2라는 것이다.
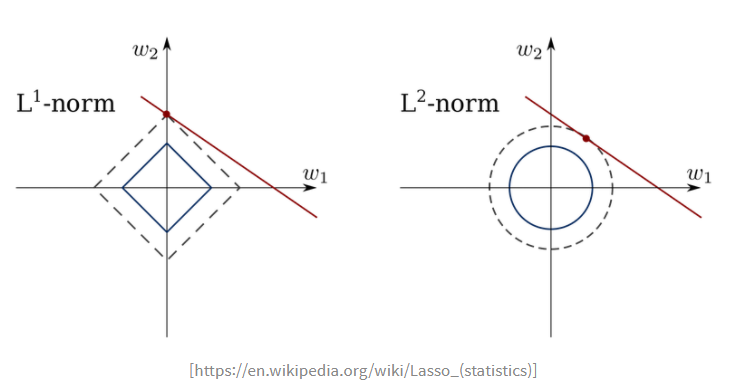
L1과 L2의 차이점을 수식 없이 직관적으로 이해할 수 있는 그림으로 L1은 베타를 이용하여 마름모 형태의 제약조건이 생기고 위의 등고선처럼 보이는 내용은 우리가 풀어야 하는 문제이다. 이 문제가 제약조건과 만나는 지점이 해가 되는데 L1에서는 몇 개의 축에서 베타값을 0으로 보낸다.
이와 다르게 L2는 베타의 제곱의 형태이기 때문에 원의 형태로 나타나고 그로 인해 0에 가깝게 감을 확인할 수 있다. 또한 제곱이 있기에 절대갑으로 L1 Norm을 쓴ㄴ Lasso보다 수럼이 빠르다는 장점이 있다.
L1과 L2 비교 코드
from sklearn.datasets import load_wine import pandas as pd import numpy as np from sklearn.model_selection import train_test_split from sklearn.metrics import mean_absolute_error, mean_squared_error wine = load_wine() wine_df = pd.DataFrame(data=wine.data, columns=wine.feature_names) target_df = pd.DataFrame(data=wine.target, columns=['Y']) X_train, X_test, y_train, y_test = train_test_split(wine_df, target_df, test_size= 0.3, random_state=101) from sklearn.linear_model import Lasso L1 = Lasso(alpha=0.05, max_iter=5) L1.fit(X_train, y_train) pred = L1.predict(X_test) print("result of Lasso") print('Mean Absolute Error:', mean_absolute_error(y_test, pred)) print('Mean Squared Error:', mean_squared_error(y_test, pred)) print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred))) print("\n\n coefficient of Lasso") print(L1.coef_) from sklearn.linear_model import Ridge L2 = Ridge(alpha=0.05,max_iter=5) L2.fit(X_train, y_train) pred = L2.predict(X_test) print("result of Ridge") print('Mean Absolute Error:', mean_absolute_error(y_test, pred)) print('Mean Squared Error:', mean_squared_error(y_test, pred)) print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred))) print("\n\n coefficient of Ridge") print(L2.coef_)
📄Output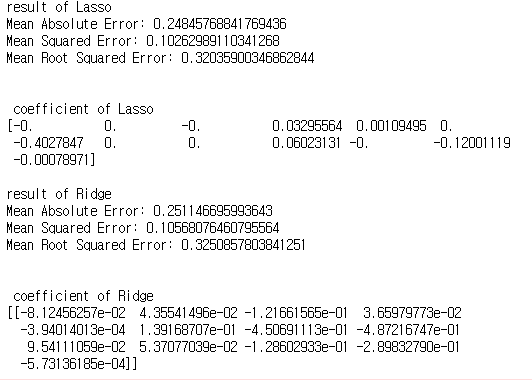
Iteration값을 5로만 설정해 보아도 L2의 문제는 Linear Regressin과 같은 값이 나오지만 L1에서는 이전의 값과 같은 값을 확인할 수 없었다.
정리하면 L1 Regularization은 가중치가 적은 벡터에 해당하는 계수를 0으로 보내면서 차원 축소와 비슷한 역할을 하는 것이 특징이며 L2 Regularization은 0이 아닌 0에 가깝게 보내지만 제곱 텀이 있기 때문에 L1 Regularization보다는 수렴속도가 빠르다는 장점이 있다.
예를 들어 A = [1, 1, 1, 1, 1], B = [5, 0, 0, 0, 0]의 경우 L1-Norm은 같지만, L2-Norm은 같지 않다. 즉 제곱 텀에서 결과에 큰 영향을 미치는 값은 더크게 결과에 영향이 적은 값들은 더 작게 보내면서 수렴 속도가 빨라지는 것이다.