[AI DEEP DIVE] DL에서 인공신경망의 기본적 이해

본 게시글은 패스트캠퍼스 [혁펜하임의 AI DEEP DIVE] 체험단 활동을 위해 작성되었습니다.
강의 링크 : https://bit.ly/3GV73FN

왜 우리는 인공 신경망을 공부해야 하는가?

혁펜하임님의 AI DEEP DIVE 강의 Ch3에 해당하는 부분이다. 이 질문의 답으로 현재 AI 부분 중 DL부분의 성능이 크게 증가해 실생활에 많이 응용되고 있다. RNN, CNN 등등에서 NN이 Neural Network의 약자이다. 이때, Neural 즉, 뉴런이 사람의 사고판단을 해주는 역할을 한다.

이를 따와 기계가 뉴런의 방식을 모방해(즉, 인공 신경망) 사람처럼 생각하게 학습한 후 Output을 내도록 하는게 DL방식의 근간이다.

그럼 이제 인공 신경망이 어떻게 이뤄졌는지 알아보자!

Bias와 Weight의 이해

시작하기 전 다음 질문의 답을 생각해보자.

"인공 신경망은 ?? 이다." (Hint : 두 글자) 정답은 아래의 글을 읽으면서 계속 유추해보자!

먼저, 아래의 뉴런의 구조를 살펴보자.

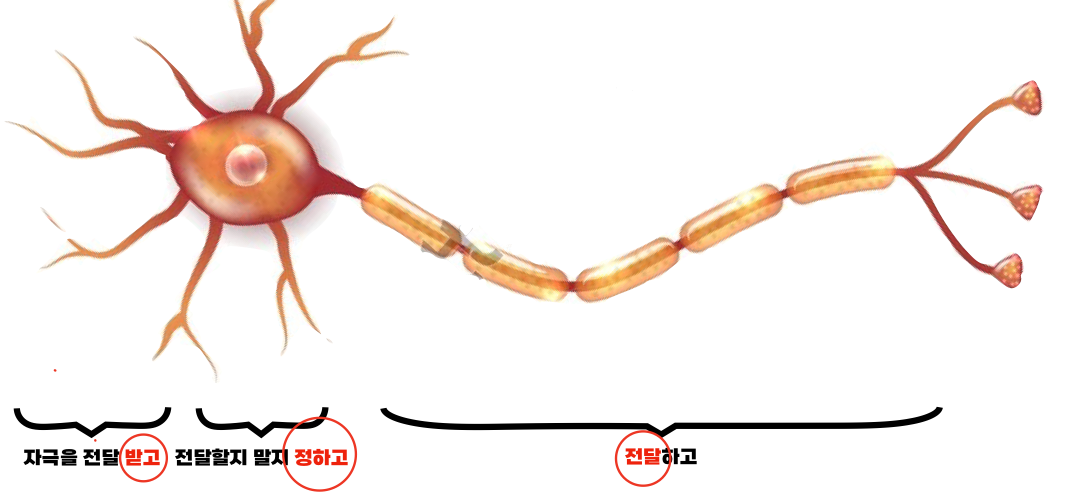
사진출처 : AI DEEP DIVE 강의자료

크게 3가지 Step이 있다.

1. 자극 받는다.
2. 전달할지 말지 정한다.
3. 다른 뉴런으로 전달한다.

이때, 아래의 그림과 같이 공학적으로 쉽게 표시하기 위해 노드(Node), 엣지(Edge) 개념이 등장한다.

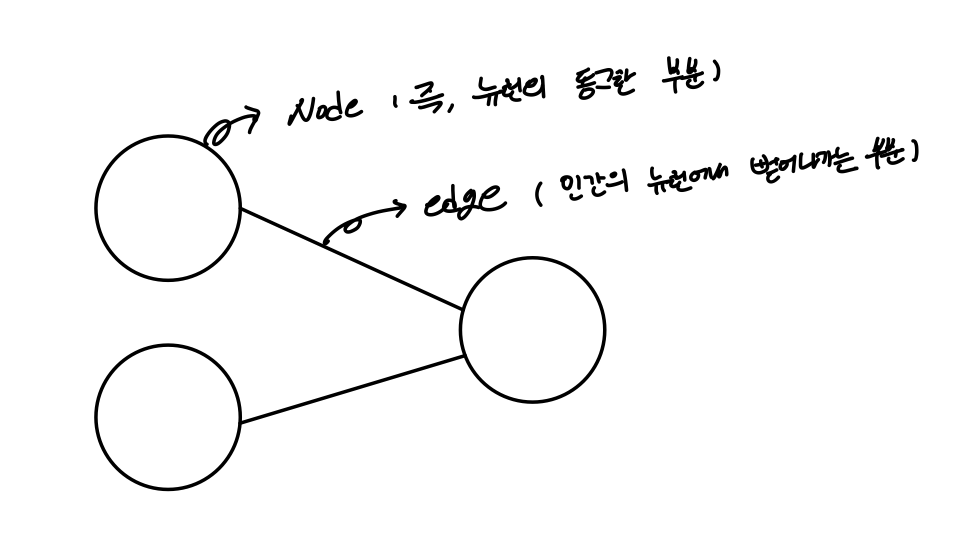
이제, 구조 설명은 끝났고 예시를 통해 weight와 bias 개념을 직관적으로 이해해보자.

아래의 그림은 두 Node의 출력값을 더한 값으로 현재 상황이 위험한지 아닌지 판단해주는 인공 신경망이다.

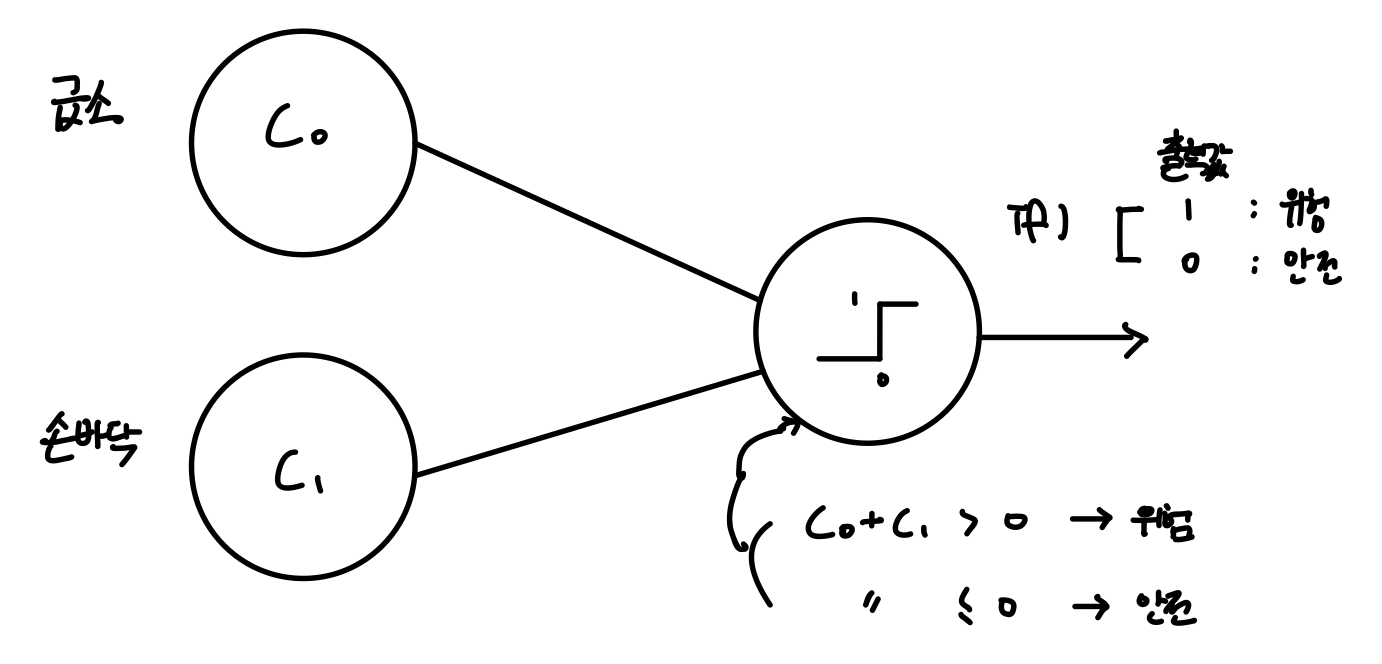
출력 Node에서 $C_0$ + $C_1$ > 0 이면 위험으로 출력, $C_0$ + $C_1$ <= 0 이면 안전으로 출력 ( 잠깐!! 위를 보고 "인공 신경망은 ?? 이다."의 답을 한 번더 생각해보자. )

Bias에 대한 직관적 이해

• Suppose
  $C_1$에 0.0000001 의 자극이 들어왔다고 해보자. (갑자기, 손바닥에 모기가 툭 치고 지나간 상황) 이때, 상황이 위험한가?? 답은 아니다. 하지만, 위에서 설계한 인공신경망의 Output은 위험으로 출력한다. 왜냐하면 출력노드는 0보다 조금이라도 큰 값이 들어오면 위험이라고 출력하게 설계를 해놓았기때문이다.

• 문제점 해결법
  이때, Bias가 등장한다. bias = -2로 Setting하자.
  이후, 출력노드로 들어오는 값의 식을 $C_0$ + $C_1$ + Bias 로 바꿔주면 0 + 0.0000001 + -2 < 0 값이 출력노드로 들어가 안전으로 출력하는 것이다.

즉, Bias는 민감도의 역할을 하는 것이다.

Weight에 대한 직관적 이해

• Suppose 1)
  Bias는 -10으로 설정되어 있고 $C_0$ = 0, $C_1$ = 10이라 해보자. (이때, 10의 파워는 펀치기계 400정도라 해보자.) 이때, 출력값이 안전인 것은 이해가 된다. 하지만, $C_0$ = 10, $C_1$ = 0 이라 해보자. 그러면 출력값이 안전으로 하는 것이 아니라 위험으로 해야하는데 $C_0$ + $C_1$ + Bias = 0 이므로 안전으로 출력된다. 어떻게 해결하면 좋을까?

• 문제 해결법
  이때, Weight가 등장한다. $C_0$의 weight를 $W_0$ = 2, $C_1$의 weight를 $W_1$ = 1이라 하자. 그러면, 출력노드에 값이 들어갈 때, $C_0$$*W_0$ + $C_1$$*W_0$ + Bias > 0 이 되어서 위험으로 출력한다.

즉, Weight는 각 변수의 중요도를 판별해주는 역할을 하는 것이다.

이제, bias와 weight가 인공신경에서 왜 쓰이는지를 알아보았다. 이 두가지의 개념이 나온 이유는 뭘까? 즉, 주어진 input에 대해 원하는 Output이 나오길 원하는 것이다.

결국, 원하는 Output이 나오려면 bias와 weight가 적절하게 셋팅되어있어야하는데 AI가 이를 스스로 알아내기 때문에 각광을 받고 있다.

출력노드에 들어있는 기호에 대한 설명

뒤에서 자세히 다룰 것인데 Activation Function으로 위에서는 Unit Step Function을 사용하였다. 이는 0이상의 값이 들어오면 1을 출력하는 역할을 한다.

인공 신경망 (Artificial Neural Network)

위에 보았던 인공신경들을 겹겹이 연결시킨 것이 인공신경망이다. 이제, DL에서는 이런 인공신경들을 layer라고 부르기로 정의했다.

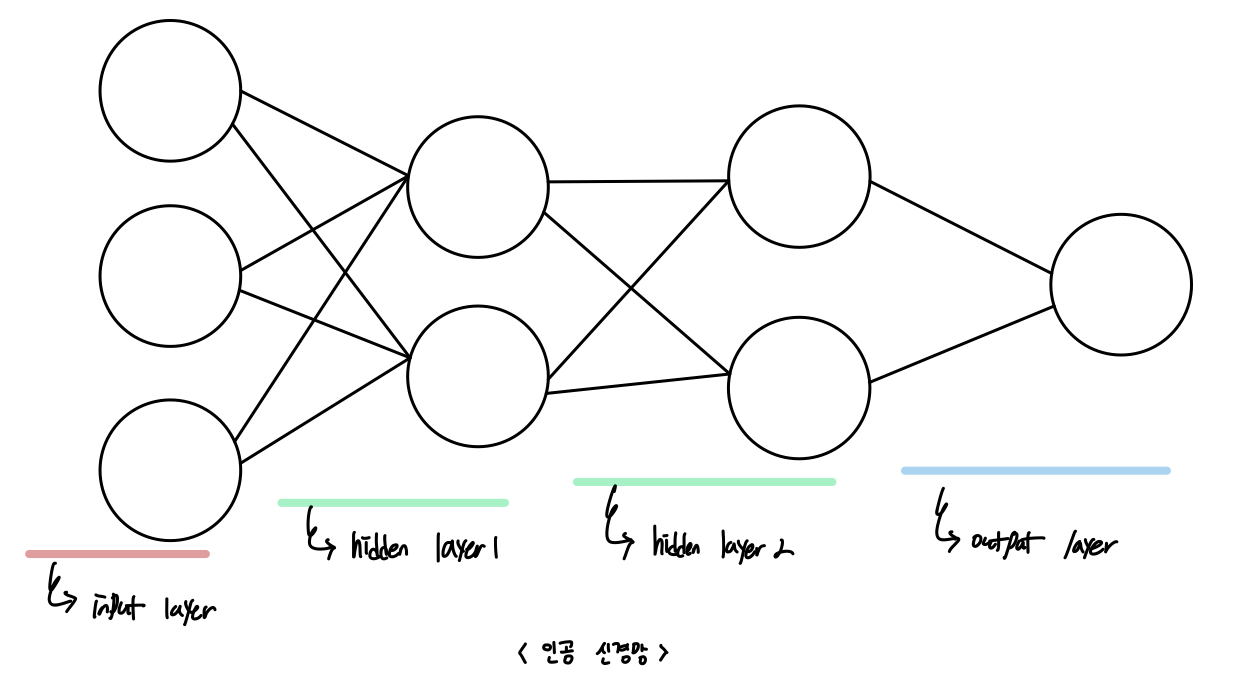
• 구성
  총 8개의 Node ( 그 중 Input Node 3개, Output Node 1개 )
  총 12개의 Edge (즉, 12개의 Weight)
  총 Bias 5개 (입력 Node는 bias 제외)

자, 쉽게 Weight과 bias의 개수를 구하는 방법은
Weight=(출력하는 Node 수 출력받는 Node 수 )+(출력하는 Node 수 출력받는 Node 수 )+ ...
Bias = 총 Node 수 - 입력 Node 수

• FC layer, MLP(multilayer perceptron)

1. FC layer
   layer가 출력하는 노드와 출력받는 노드가 서로 싹 다 연결되어 있는 것을 말한다.
   즉, 출력하는 노드가 3개 출력받는 노드가 2개라고 가정하면 Edge가 총 6개 있어야한다.

2. MLP
   모든 layer들이 FC layer이어야한다. 이때, 약자에서 perceptron이 등장하는데 이는 출력노드의 활성화함수(즉, activation function)이 Unit Step Function을 의미하는데 MLP에서는 모든 활성화함수를 사용하는 인공 신경망을 의미한다.

선형회귀 (Linear Regression)

선형회귀는 선형모델로 훈련된 기계에 Input data를 넣었을 때 적절한 출력을 내도록 하는 것이다.

Ex) 선형모델로 훈련된 기계에 사람의 특성 키가 주어지면 몸무게를 출력해주는 함수가 있다하자. 이때, 키가 $X_i$, 몸무게가 $y_i$라고 설정하면 y = aX + b에 입력하면 적절한 값이 나와야한다.

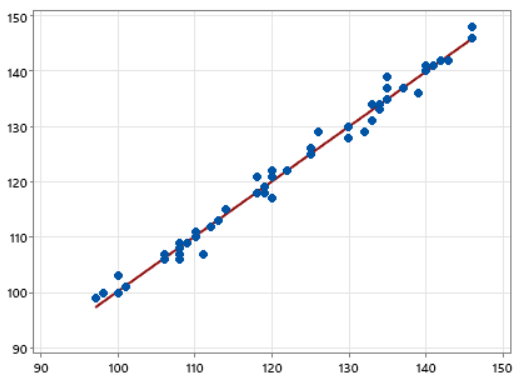
그러면, 이때 적절한 값이 나오기위해 기계는 어떤걸 훈련했는가 바로 a,b를 훈련한 것이다!!

최적의 a,b 찾기

최적의 a,b를 찾는다라는 말은 보면 최적(좋고 나쁘다)를 판단 할 수 있는 기준이 필요하다. 이때, 등장하는 것이 바로 Loss Function이다. 이는 다양한 방식이 있는데 큰틀을 말하면 실제값과 예측값의 Error에 연산을 취하고 더한 값을 말한다. 즉, Loss Function이 제일 작은 값을 갖는 a,b를 찾는 것이 목표다.

그러면, 이제 Loss Function이 무엇인지 왜 제일 작은 것을 찾아야하는지 알아보았다. 근데 어떻게 error를 구할 것인가??

일일이 Naive하게 대입해서 구하기엔 데이터 양이 작거나 특성이 작으면 할 수는 있지만 시간이 매우 오래걸리다... 그래서 여기서 등장하는 gradient descent방법이 소개되는데 이에 대해 알아보자!

Gradient Descent (경사 하강법)

각 특성마다 Gradient를 구해 본래의 값에다가 빼주면서 업데이트를 진행한다.

근데, 이것이 어떻게 최적의 a,b로 가는지 알 수 있을까?? 이를 정확히 알기 위해서는 gradient는 항상 가파른 방향을 향한다는 성질을 알아야한다. ( 이는, 수학적 지식을 꽤 설명해야해서 따로 포스팅을 통해 설명 해보겠습니다. )

그래서, 특성마다 미분을 통해 제일 가파른 방향을 구하고 이를 빼주면 Loss가 제일 작은 특성의 가중치를 알 수 있다. 즉, 아래의 식은 i+1번째 x를 업데이트 시켜주는 과정인데 i번째 x를 넣고 미분을 해서 그레디언트를 구하고(최소로 가는 방향) 그것에 $\alpha$를 곱해 빼준다.

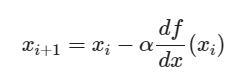
여기서, $\alpha$가 등장하는데 이는 learning rate라고 불린다. 이게 존재하는 이유는 아래의 문제 상황을 줄테니 생각해보기 바란다.

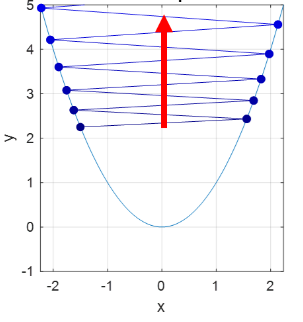
Ex 1) 이는 학습률이 클 때 발생하는 문제인데 우리의 목적인 Min으로 다가가지 않고 발산해버리는 모습이다. 아래의 그림으로 확인 할 수도 있고 식으로도 확인해보자.

$x^2$ + $y^2$ 식이 있다 가정하고 그레디언트를 구하면 $G^T$ = [2x, 2y]이다. 식을 업데이트 해보면 [1,1] - [2,2] = [-1, -1]이다. 다시, 이 과정을 반복해 업데이트해보자 그러면 [-1, -1] - [-2, -2] = [1,1]이다. 이를보면, 다시 [1,1]로 돌아왔다. 왜냐하면, 방향은 감소하는 방향이 맞다. 하지만, 크기가 지나치게 커서 아래의 그림과 같이 반대로 확 넘어가는 것이다.

이 문제를 해결하기위해 학습률이 등장했고 아래의 문제의 경우에는 학습률을 줄여줘야한다.

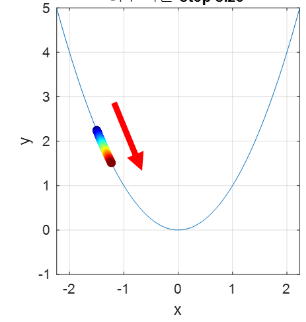
Ex 2) 그러면 위에 같은 상황을 만들지 않기위해 학습률을 매우 줄여버리면 되겠네 생각하시는 분들도 있을 것같다. 하지만, 그렇게 해버리면 아래의 문제가 발생한다. 학습이 매우 더디게 진행되는 문제에 봉착하게 되어서 적절한 학습률이 필요하다.

Gradient Descent의 두 가지 문제점

1. Local Minimum
   데이터들의 분포가 모두 이차함수처럼 한 개의 최솟값을 갖는게 아니다.
   4차함수처럼 극소값을 2개갖는 분포를 가질 수도 있다. 이럴때, 초기 값을 어디서 시작하냐에 따라 경사하강법은 Local Minimum 문제점을 가진다.

Local Minimum이란 우리가 Loss가 최소라고 생각하는 파라미터들이 실제로 알고보면 최소가 아니라 지역적으로 최소인 지점이다. (즉, 더 좋은 파라미터들이 존재한다.) 이 지점을 벗어나서 전역적으로 최소인 지점으로 찾아가면 좋지만 Local minimum으로 갈수록 그레디언트 값이 0으로 다가가서 더이상 움직이지 않는다. 아래의 그림을 보며 이해해보자.

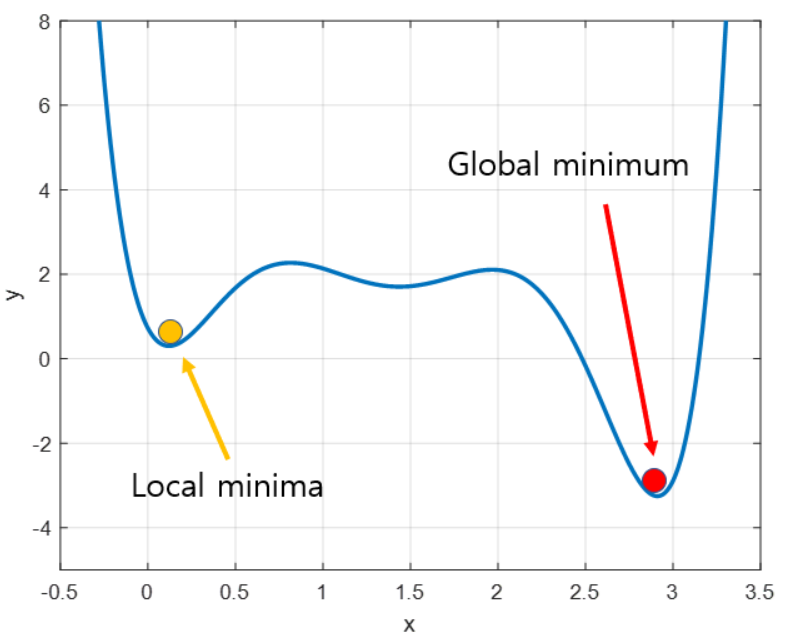
초기 값을 (-0.2,5)에서 시작했다고 가정하자. 그러면 우리는 경사하강법을 통해 노란색 점에 다가가면서 학습을 진행하고 그레디언트도 0으로 다가가 학습이 종료된다.
하지만, 우리가 찾고 싶은 것은 빨간색 점이다. 이를 찾지못하고 훈련이 종료가 되어 문제가 발생하는 것이다.

2. 모든 특성을 너무 신중하게 고려

그레디언트를 구할때 모든 특성의 기울기를 모두 구해 값을 넣어서 계산하여 방향을 정하기 때문에 너무 신중하다는 문제가 있다. 즉, 특성이 10000개 이상이 되면 모든 그레디언트를 구해 값을 넣어 방향을 설정해 시간이 매우 오래걸린다.

Weight Initialization

아래의 세 가지 가중치 초기화 방식은 공통적으로 Random하게 잡은 값이 0 근처이다. 직관적으로 생각해보면 한 특성의 가중치가 매우 커지는 것보다 0으로 되어있을때 학습이 잘 될것이다. ( Training 데이터를 학습하면서 특성에 맞게 가중치를 업데이트 하기때문에!!)

아래의 w vector는 Uniform or Nomal random variable인데 uniform RV의 평균은 U[a,b] = (a+b)/2이다. 그리고 Nomal RV는 모수로 평균과 분산을 주는데 아래의 3개의 식 모두 평균은 0으로 고정이 되어 있는 것을 확인 할 수 있다.

1. LeCun
   

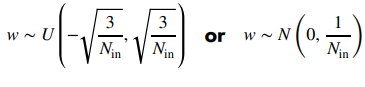
   사진 출처: AI DEEP DIVE

2. Xavier(주로 Activation Function이 Sigmoid, tanh)
   

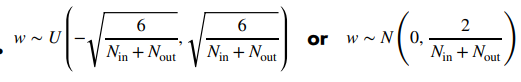
   사진 출처: AI DEEP DIVE

3. He(주로 Activation Function이 ReLU)
   

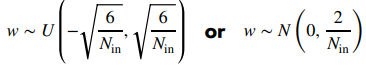
   사진 출처: AI DEEP DIVE

SGD : GD(경사하강법)의 문제점을 보완한다.

제목으로 이미 SGD방법은 GD의 문제점을 보완한다고 알려주었다. 그렇다면 GD의 문제점 2가지가 무엇인지 떠오르는가??

1. 너무 섬세하게 방향을 결정한다.
2. Local minimum에 빠질 수 있다.

( 만약, 두 가지 문제점이 떠오르지 않는다면 위에 포스트 내용을 한번 더 읽기를 권한다! )

GD의 문제점 1 보완

섬세한 방향결정의 문제점은 '계산속도'(즉, 시간)이다. SGD도 그레디언트을 구해 가중치를 업데이트하는 방식은 동일하지만 GD와 차이점은 GD는 모든 데이터를 이용해 구하고 SGD는 Random하게 하나의 데이터를 사용해 업데이트한다.

아래의 그림을 보면 비교해보자.

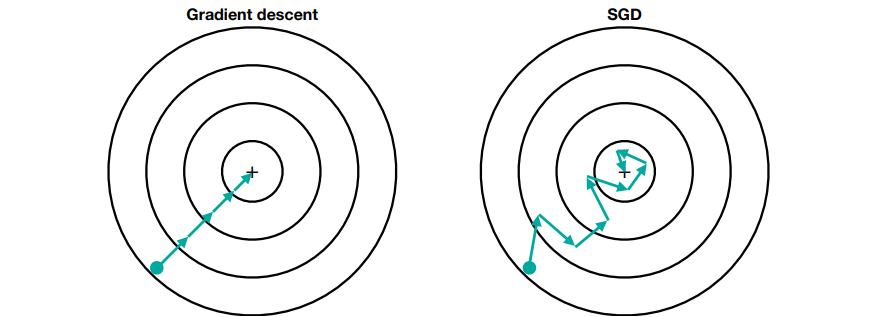
사진출처: AI DEEP DIVE 강의

GD는 초기값(민트색 점)에서 최적의 값으로 다가갈 때 모든 데이터를 다 사용해 그레디언트를 구하므로 +로 갈때 둘러가지않고 한번에 바로간다. 하지만, SGD는 한 개의 데이터만 사용하기때문에 Loss가 작아지는 방향이긴하지만 GD보다는 둘러간다.

혹시, 그림만 보고 GD가 SGD보다 화살표 수가 작은데 왜 더 빠르지라는 의문을 가질 수 도 있다. 이는 GD에서 한 화살표를 정할때 계산량이 SGD의 화살표의 방향을 결정하는 계산량 차이를 보면 쉽게 알 수 있다.

Ex) Sample이 100,000개 있다고 가정하자. Loss Function을 통해 가중치를 업데이트 할 때 GD는 화살표 당 100,000 연산이 필요하지만 SGD는 1번의 연산이 필요하다.

즉, 그림에서는 GD는 400,000번 SGD는 8번의 연산을 진행한다. 매우 차이가 큰 것을 확인할 수 있다.

GD의 문제점 2 보완

Local Minimum에 빠질 수 있는 문제가 있다. 하지만, SGD가 이 문제를 100% 해결해 주지않고 Local Minimum을 빠져나갈 수 있는 기회가 존재하는 것이다. GD는 만약 초기점이 Local Minimum에 빠지는 경우에 있다면 100이면 100 Local minimum으로 간다. 하지만, SGD는 Random하게 뽑아진 데이터 하나가 이를 해결 할 수 있는 Key가 될 수도 있다.

아래의 그림을 통해 설명해보면

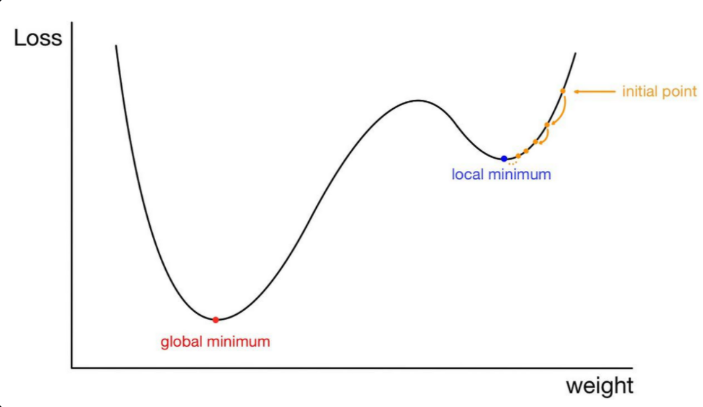
학습률이 그림과 같이 셋팅되어있다면 GD는 무조건 Local Minimum(파란색점)에 빠진다. 하지만, SGD는 Random한 Data를 운좋게 뽑으면 탈출가능하다.

Mini-batch SGD

하지만, SGD는 1개의 데이터만 보고 업데이트하기 때문에 이번에는 GD의 정반대로 너무 성급하게 방향을 결정하는 문제가 발생한다.

따라서, Random한 한 개의 데이터 말고 개발자가 직접 정한 batch size 갯수만큼 데이터를 보고 방향을 결정하는 것이 Mini-batch SGD이다.

아래의 그림은 한 논문에서 실험한 결과이고 X축이 batch size 크기이고 Y축이 Loss값이다. batch size를 8k정도 하는 것이 적당해보인다. 그리고 batch size를 키울 수록 error가 매우 커지고 있다. 이에대한 이유는 혁펜하임 강사님이 설명하시기를 배치 size를 키울 수록 Local Minimum에 빠질 확률이 매우 올라가기 때문일 것이라 예측했다.

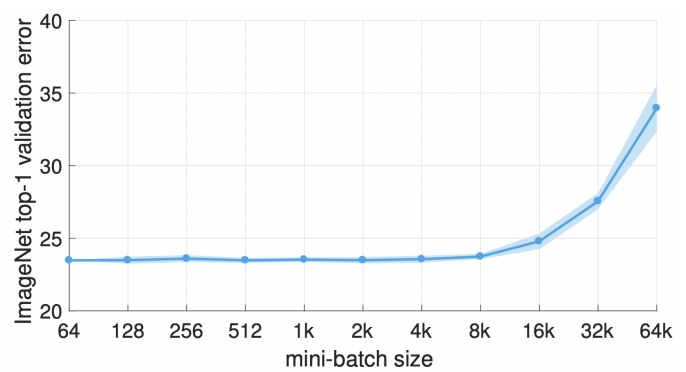
그리고 batch size를 키울때 2가지 사항을 지켜줘야 Loss를 아래와 같이 유지해 줄 수 있다.

1. learning rate도 같이 정비례로 키워줘야한다. 즉, BS를 2배올리면 LR도 2배를 올려야한다. 그래야, loss비율을 아래의 그래프와 같이 맞춰줄 수 있다.

2. 초기 learning rate를 warm-up을 해줘야한다. 처음에는 작게하고 점점 올려가는 형식 이 warm up 단계가 끝나고는 learning rate scheduling을 해서 적절한 학습률을 선택해야한다.

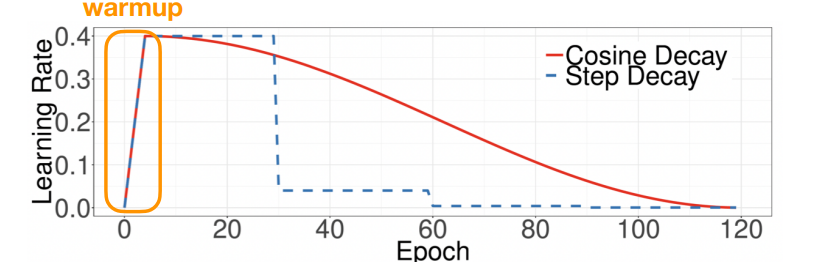
Epoch & Batch size & Learning rate

1. Epoch : 전체 데이터를 몇 번 돌 것인지
2. Batch size : 한 번 훈련시에 몇 개의 데이터를 볼 것인지
3. Learning rate : 파라미터 업데이트시에 얼만큼 이동할 것이지

위 3개를 포함해 (활성화 함수, Loss 함수 등등) 모두 개발자가 정해줘야하는 값으로 이러한 값들을 하이퍼 파라미터라고 부른다. 그 외에 weight bias 등등은 명칭이 파라미터로 기계가 학습하면서 자동적으로 업데이트하는 값이다.

momentum, RMSprop, Adam (Adaptive Moment Estimation)

momentum, RMSprop 각각이 어떻게 최솟값을 가지는 값으로 다가가는지 살펴보고 이 둘의 기능을 합친 Adam의 설명하겠습니다.

momentum

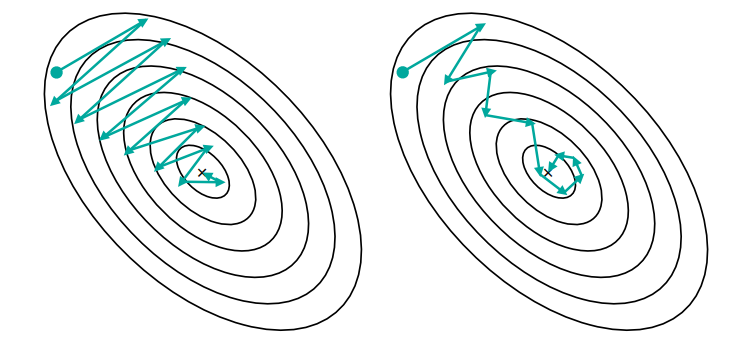
아래의 그림은 mini batch SGD와 momentum의 최솟값으로 찾아가는 과정을 나타낸 그림이다. 첫번쨰 그림인 mini batch SGD는 이전 그레디언트를 통해 이동한 방향으로의 힘이 고려되지 않는다. 하지만, momentum은 이전의 방향을 고려해 다음을 업데이트한다. 즉, 그레디언트를 누적하며 관성이 고려되는 것이다.

관성이란 버스에 탔을때 갑자기 버스가 멈추면 몸이 버스가 이동했던 방향으로 쏠리는 것을 느낄 수 있을 것이다. 바로 그것이 관성이다.

RMSprop

파라미터를 업데이트 할 때 learning rate를 조절한다고 생각하면 된다. 경사가 급한 곳은 한 번에 파라미터를 많이 업데이트하면 위험하다. 그래서 비교적으로 작게 변경하고 경사가 완만한 곳은 비교적 위험하지 않기때문에 업데이트를 과감하게 진행한다.

즉, learning rate를 파라미터마다 개별적으로 준 것이다.

Adam

위 두가지 momentum과 Adam을 섞어 만들었다. 아래의 식을 살펴보자!

사진출처: AI DEEP DIVE

여기서, 주의해서 볼 식 3개는 $m_t$, $v_t$, $\theta_t$이다.

$\theta_t$ 는 기존에 알고있던 식에서 $m_t$, $v_t$ 가 변경된 것이다. 이제 하나씩 의미를 살펴보자!

먼저, 가정으로 $\beta_0$=$\beta_1$=0.5라 하자.

1. $m_t$

$m_t$식에서 t에 1을 대입한다.

$m_1$ = 1/2$m_0$ + 1/2$g_1$ = 1/2$g_1$ (t = 1)

$m_2$ = 1/2$m_1$ + 1/2$g_2$ = 1/2(1/2$g_1$) + 1/2$g_2$ = 1/4$g_1$ + 1/2$g_2$ (t = 2)

$m_3$ = 1/2$m_2$ + 1/2$g_3$ = 1/2(1/4$g_1$ + 1/2$g_2$) = 1/8$g_1$ + 1/4$g_2$ + 1/2$g_3$ (t = 3)

t가 커져도 이전 그레디언트를 반영하는 모습을 찾아볼 수 있다. 이게 위에서 말한 관성을 고려한 방법이다.

1. $v_t$

$v_t$는 위에 식에서 $m_t$를 $v_t$로 바꾸고 gradient를 제곱한 것이다. 이때, gradient를 제곱한 이유는 크기를 고려하기 때문에 그런 것이다. $\theta_t$에서 $v_t$에 루트를 씌어서 나눠주기때문에 그레디언트 크기가 큰 것은 작게 이동하고 그레디언트 크기가 작은 것은 더 많이 움직여주는 것이다.

Training set vs Test set vs Validation set

Model을 훈련시킬 때 주어진 데이터를 잘나눠야한다. 결론적으로 3가지를 나눠야한다. Model의 파라미터 훈련(Training set), 모델의 하이퍼 파라미터 훈련(Validation set), 모델의 최종성능 검증(Test set)

먼저, Model을 훈련 시켜야하기 때문에 Training set이 존재하는건 부담없이 받아들인다. 이때, Test를 나누는 이유를 직관적으로 생각해보자.

우리는 최종적으로 모델을 출시할때 일반적인 상황에서 성능이 잘나오길를 원한다.
근데 Test set을 나누지않고 모두 학습을 시켜버리면 검증단계에서 모델이 몇번 돌아본 데이터에 대해서는 잘맞추는게 당연하다.

그래서, 모델을 최종적으로 검증할 때 딱 한번만 보게 빼놓는 것이 Test set이다. (일반적 성능 측정)

근데, 이러면 우리는 모델을 학습하는 도중에 Test를 하면서 하이퍼 파라미터를 변경하고 싶다. 그렇지않으면 데이터가 많아 모델이 훈련하는데 3일이 걸린다고 가정하자.

그러면, 3일동안 훈련하고 안좋아서 하이퍼 파라미터 수정하고 또 3일 기다리고 또 안좋아서 3일 기다리고 매우 비효율적이다. 그래서 훈련중간에 test를 할 수 있는 validation set을 정해 중간중간 검사를 한다.

• 실생활 예시
  Training set: 교과서 연습문제
  Test set: 대학 수능
  Validation set: 모의고사

K-Fold Cross Validation

이 방법은 훈련할 데이터양이 적을때 유용하게 쓰이는 방식인데, 아래의 사진과 같이 Validation set을 나눈다.

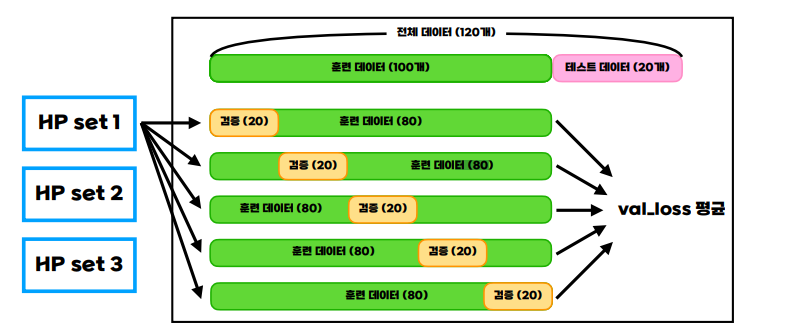
사진출처: AI DEEP DIVE

그림에서 HP set1 은 하이퍼 파라미터 셋으로 간단하게 learning rate가 0.1, HP set2는 learning rate가 0.01, HP set3는 learning rate가 0.001 이런식으로 하이퍼 파라미터를 바꾼 집합이다.

이 집합에서 그림과 같이 검증셋을 하나만 하면 과대적합으로 펴향이 생겨버려서 훈련 set를 각기다르게 설정해버리는 것이다. 이후, val loss의 평균이 가장 적은 하이퍼파라미터 셋을 고르면 된다.

#패스트캠퍼스혁펜하임 #혁펜하임 #혁펜하임AI #패스트캠퍼스 #혁펜하임강의 #AIDEEPDIVE #ai강의 #혁펜하임강의후기