[AI DEEP DIVE] 이진분류와 다중분류

본 게시글은 패스트캠퍼스 [혁펜하임의 AI DEEP DIVE] 체험단 활동을 위해 작성되었습니다.
링크 : https://bit.ly/3GV73FN

이중분류

Model이 Training Data로 가중치와 편향을 학습하고 새롭게 들어온 Sample이 Class 2개 중에 어느 곳에 속하는지 알려주는 것이다. 예시를 통해 살펴보면 쉽게 알 수 있다.

Ex) 사진을 한 장 주었을 때(새로운 Sample) 이 사진이 고양이인지(class1) 강아지인지(class2) 분류해라.

Activation Function이 unit-step function일 때 이중분류

layer을 거치면서 "가중치를 곱하고 편향을 더하고 activation"과정을 반복 후에 마지막 node에서 Activation function이 unit-step function이라하자.

then, 들어온 값이 0초과이면 1로 출력 0이하이면 0으로 출력한다. 이때, 1과0은 클래스 종류이다. (위의 예시에서 강아지 고양이 부분이다.)

근데 이 방식은 2가지의 문제점이 있다.
1. 미분이 불가능하다.
2. 너무 빡빡하게 분류를 해버린다.

미분이 불가능하다는 말은 Gradient descent를 사용하지 못한다. 그리고 너무 빡빡하다는 부분은 다른 예시를 이용해 설명해보겠다. 키와 몸무게를 입력값으로 주면 이중분류로 다이어트를 해야하는지 안해도 되는지 분류해주는 Model이라하자.
이때, 출력 node에 activation function unit step function을 쓴다고하자.

빨간색 체크된 곳의 사람은 빼지않아도 되는데 빼야한다고 빡빡하게 분류한 것이고
빨간색 체크된 곳의 사람은 찌지않아도 되는 쪄야한다고 빡빡하게 분류한 것이다.

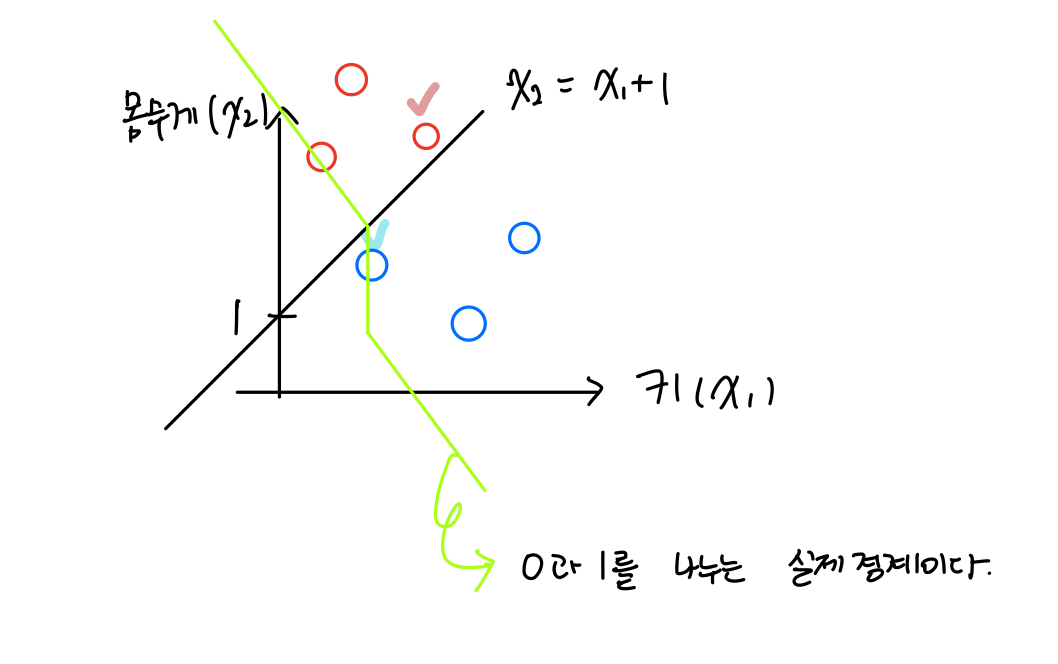
추가적으로, unit-step function의 실제 분류경계를 보면 선형적이 아니라 $X_2$ =$X_1$+1을 기준으로 급격하게 꺾이는 것을 확인할 수 있다.

즉, 위에 2가지 단점을 보완하기 위해서 Sigmoid함수가 등장한다.

Activation Function이 Sigmoid일 때 이중분류

Sigmoid Function

• S(X) = 1/1+$e^x$ 이다.

이 S(X)의 값은 범위가 [0,1]값을 가진다. unit-step function은 0 or 1에 비해 매우 표현력이 높아졌다. 그리고 이 값은 확률값으로 생각이 가능하다.

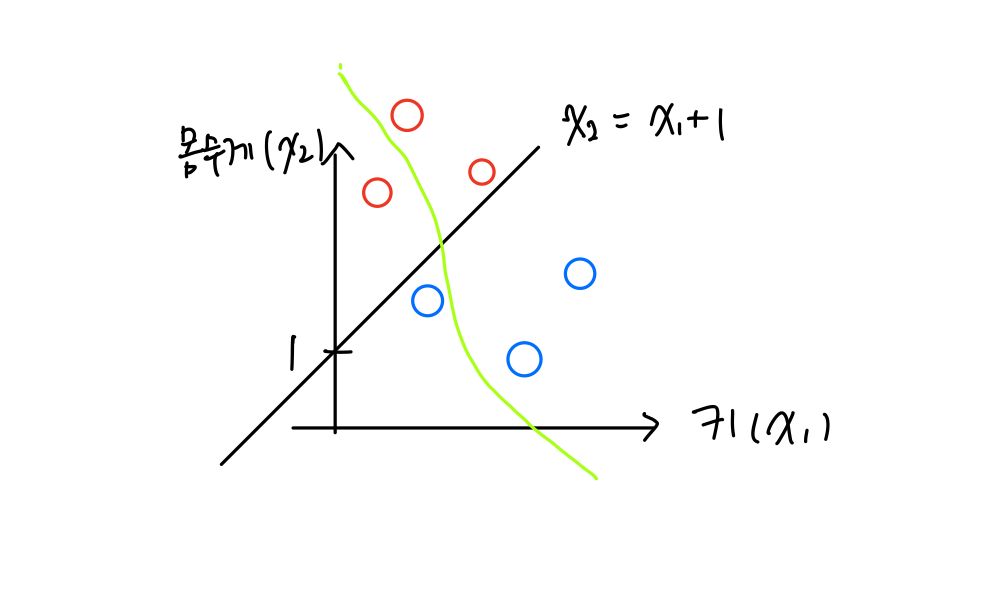
경계가 좀 더 부드러워진 것을 확인할 수 있다.

또 하나의 장점을 소개하겠다.

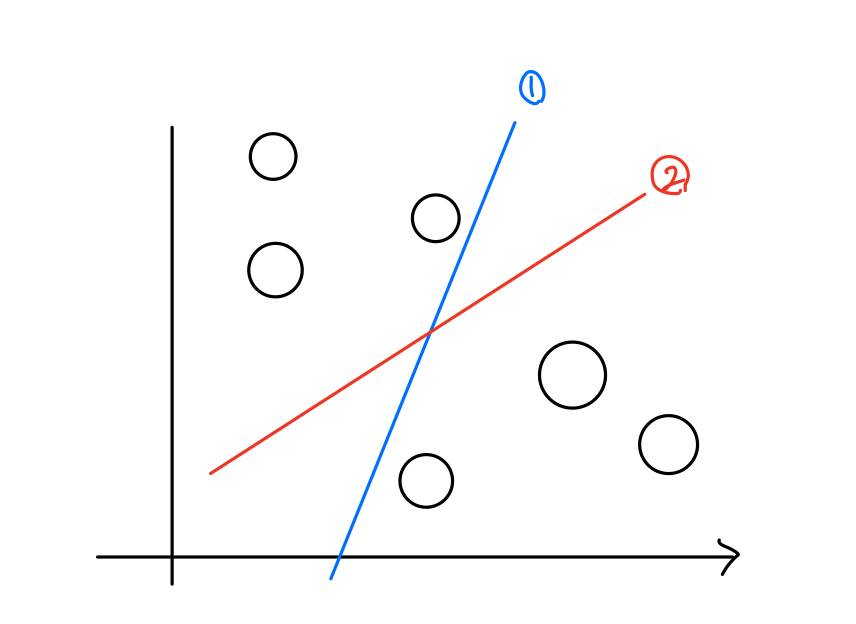
이때, 출력노드의 activation이 unit step function이면 1,2번의 성능이 동일하다고 판단한다. 하지만, 출력노드의 activation이 Sigmoid이면 1,2번의 성능이 다르다. 왜냐하면, 1번의 결정경계선에 붙은 노드들은 값이 0.5에 가깝게 나오지만 2번의 결정경계선은 더 높은값이 나온다.

Sigmoid의 Loss function 전개과정

Let class가 2개(강아지, 고양이)가 있다. 그리고 사진을 넣었을 때 Model이 강아지를 잘 맞추게 짜야한다. model을 훈련한다는 것은 가중치와 편향을 업데이트 하는 것이다. (하이퍼파라미터는 잘 주어져있다고 가정한다.)

업데이트를 하려면 Loss function을 알아야한다.

결론적으로 q^y * (1-q)^(1-y)를 최대화해야한다. 왜냐하면, 정답 label이 1이면 강아지를 잘맞춰여하므로 q를 최대화해야한다. 정답 label이 0이면 고양이를 잘맞춰야하므로 1-q를 최대화해야한다. (이때, q는 강아지를 예측한 확률이다.)

따라서, 훈련을 위의 식으로 진행해주면 된다. 그리고 데이터를 넣는 것은 독립시행이므로 P(AB)= P(A)P(B)이다. 따라서, 위의 최대화 하는 식을 sample하나씩 넣은 것을 곱해주어여한다.

$q^1$ $y^1$ (1-$q^1$) $y^1$ x $q^2$ $y^2$ (1-$q^2$) $y^2$ x $q^3$ $y^3$ (1-$q^3$) $y^3$ x ... 을 최대화 해야한다.

근데 sample을 집어넣어서 나온 값들이 모두 0-1사이의 값이라서 데이터가 많아질 수록 값이 0으로 다가간다. 그래서 log를 취해준다. 이때, log를 취해도 되는 이유는 단조증가함수라서 최대값을 구하는 과정이 log를 취한 것과 취하지 않은 것은 동일해서 가능하다.

∑( log ($q_n$ ^ $y_n$ x (1 − $q_n$)^(1−$y_n$) ) (이러면, log성질 때문에 곱이 플러스로 바뀐다.) 그리고 이는 최대화 하는 q를 찾는 것이 목적이니 Loss function은 최소화 개념이 들어가야해서 Loss = - ∑( log ($q_n$ ^ $y_n$ x (1 − $q_n$)^(1−$y_n$) )이다.

sigmoid는 logistic regression이라 불린다. 그리고 logistic regression은 한줄로 설명하면 logit을 linear regression 한 것이다.

이때, logit은 승산에 로그를 취한 것으로 $l$ = $log\frac{q}{1-q}$이다.(이때, $l$은 들어오는 값 q는 강아지가 나오는 확률값)
이제, q에 대한 식으로 만들어보자. $\frac{q}{1-q}$ = $e^l$, $\frac{1-q}{q}$ = $e^-l$ 쭉쭉 풀어주면 d = 1/1+$e^l$ 식이 나온다.

MSE를 쓰지않고 새로운 Loss함수를 도입한 이유

Let 강아지 사진을 1장 입력했다고 가정하자. 이때, MSE는 (q-1)^2, 새로운 Loss Func은 -log q이다. 이는 새로운 func이 더 민감하게 조치한다. 그래프를 생각해보면 쉽게 이해가 가능할 것이다. q가 1로 예측하면 에러는 0으로 동일하지만 0으로 예측했을때, MSE의 오차는 1 sigmoid의 loss func는 무한대이다.

그리고 마지막 sigmoid 통과 직전 weight 에 대해 Loss function의 개형이 (q-1)^2라면 non-convex, -log q라면 convex이다. 전자는 local minimum에 빠질 수가 있다.

딥러닝의 뿌리이론

위의 두 Loss Function은 MLE를 기반으로 가지치기 된 것이다. 이 두가지로 제한되는 것이 아니라 softmax Loss function등등의 모든 Loss function도 MLE를 기반으로 가지치기 된 것이다.

베르누이 분포라고 가정, 머신의 출력을 강아지일 확률 로 삼고 NLL 식 유도

베르누이 분포는 확률변수가 0 or 1만 가지는 분포이다. 확률변수 X의 pdf는 f = q^y * (1-q)^(1-y)이다. (이때, X는 사진이 강아지이다. 1이면 강이지 0이면 강아지가 아니다.)

여기서, 전체에 대해 NLL(negative log liklihood)하면 -log ($\sum$ q^y * (1-q)^(1-y))이다.

가우시안 분포라고 가정, 머신의 출력을 평균 값으로 삼고 NLL 식 유도

이번에는 데이터의 분포가 가우시안 분포이면 pdf가 f = 1/sqar(2$\pi$$\sigma$)$e$ ^((x-$\mu$)^2/ 2$\sigma$^2)이다. 이를 전체 데이터에 대해 NLL하면 -log($\sum$(x-$\mu$)^2) (상수값은 다 제거했다. 왜냐하면, 아까 보았던 최솟값을 구할때는 단조함수이면 크기는 영향을 받지않기 때문이다. 줄어드는 방향은 같기 때문에)

따라서, 현재 문제의 종류가 이진분류라 분포가 베르누이 분포를 가지고 분류하는 것이 좋은 스코어를 갖는다. 결국 학습은 w에 대한 MLE이다.

다중분류

softmax

softmax는 클래스가 2개이상의 분류가 필요할 때 사용된다. 아래의 그림으로 동작과정을 살펴보자.

Ex) class가 총 3개(강아지, 고양이, 말)이 있고 사진이 들어갔을 때 어떤 동물인지 분류해주는 모델이 있는데 입력층은 30000X1 크기이고 Hidden layer 1개 출력 layer이 있다하자. 그러면 아래의 그림과 같이 나타낼 수 있다. (총 파라이미터 갯수는 90003개이다.)

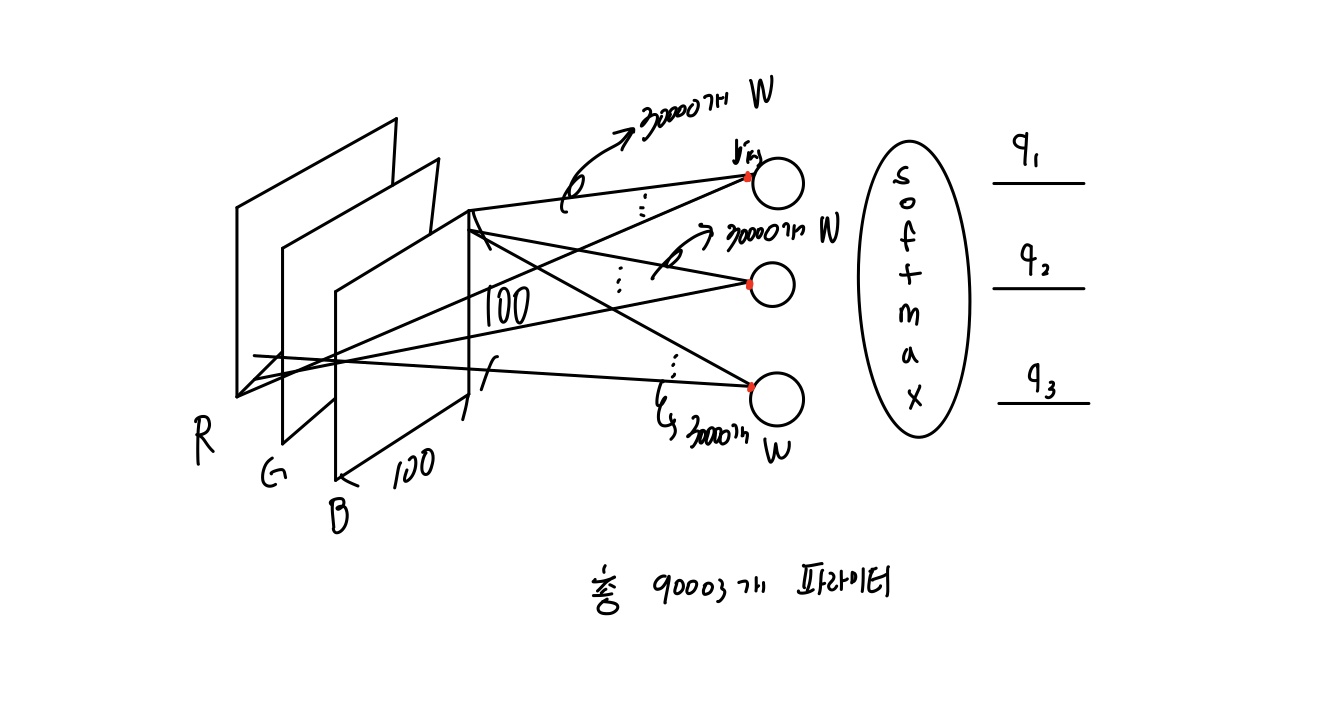
$x_1$, $x_2$, $x_3$가 softmax를 통과하면 아래의 값이 나온다. 이 값이 나온 두 가지 중요한 배경이 있다. $q_1$, $q_2$, $q_3$를 다 더했을때 값이 1이어하고 $q_1$, $q_2$, $q_3$의 각각의 값의 범위가 [0,1]이어야해서다.

아래의 식은 위 두 조건을 다 만족한다.

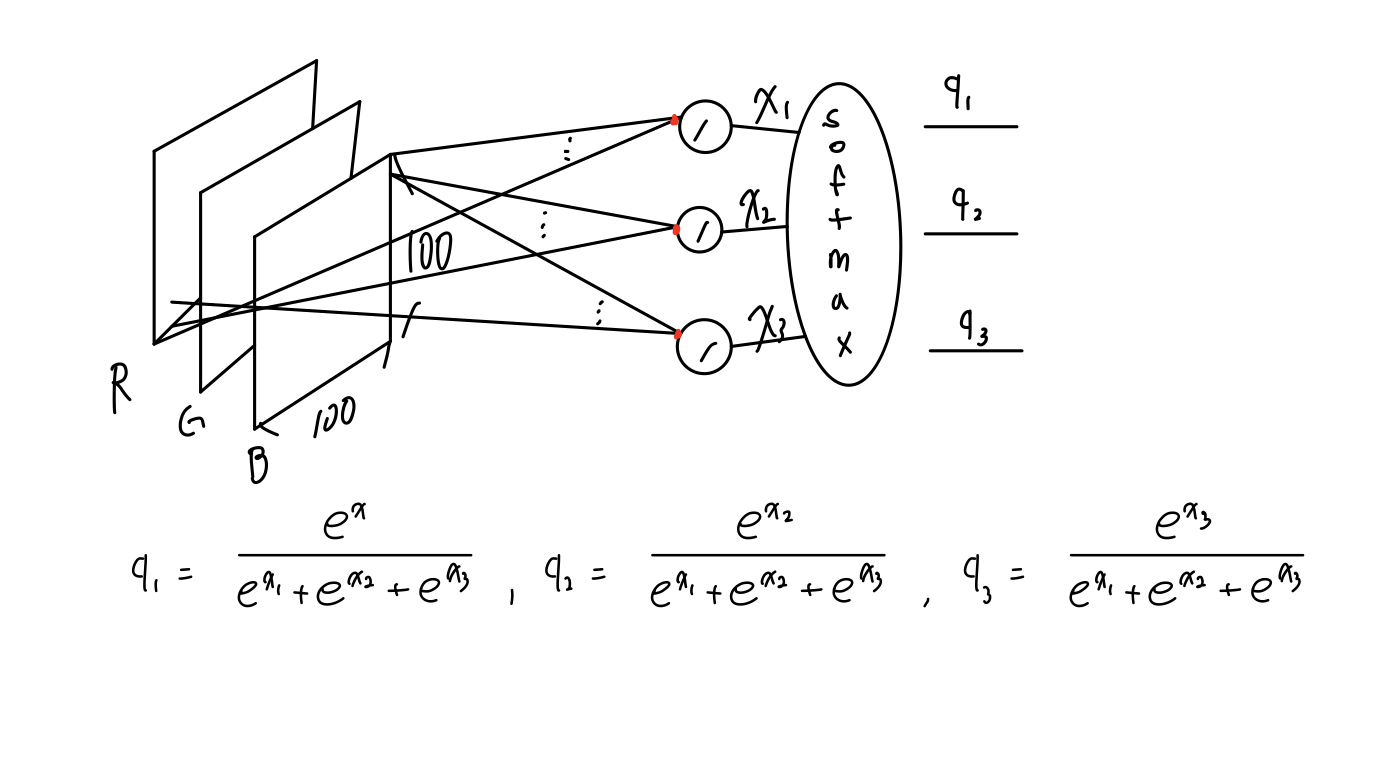
왜 $e^i$ / ($e^1$ + ... $e^n$)이어야만 하는가?

아래의 두 식은 불가능한가??

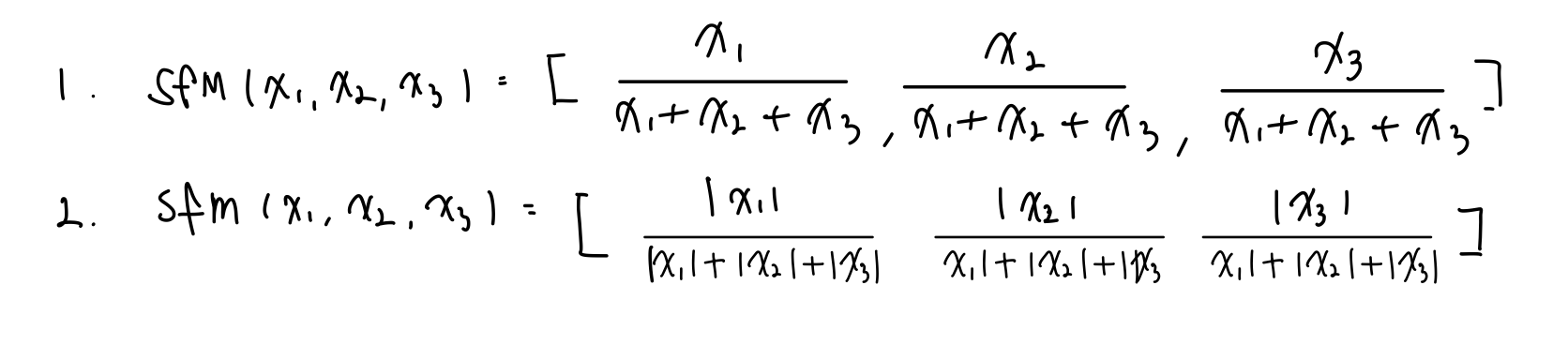
1번의 문제점은 각각이 음수가 나올 수 있다.

2번의 문제점은 미분이 불가능하다는 것은 0값에서만 예외처리를 해주면 해결이 가능한데 다른 중요한 이유가 있다.
$x_1$ = 1, $x_2$ = 1, $x_3$ = 1
$x_1$ = 1, $x_2$ = -1, $x_3$ = 1
$x_1$ = 1, $x_2$ = 1, $x_3$ = -1
...
$x_1$ = -1, $x_2$ = -1, $x_3$ = -1
값이 모두가 같은 값을 가진다. 이는 표현력이 $e$보다 떨어진다고 할 수 있다.

softmax대신 각각의 입력값에 대해 sigmoid를 쓰는 것은?

이는 문제자체가 다른 것이다. 우리가 표현하고 싶은 것은 해당 사진이 어떤 동물에 가까운지 1개만 정해주는 반면 이 문제는 각각의 class에 대해 사진안에 동물들이 있는지 없는지 알려주는 것이다. 이 문제는 Multi-label classificatio로 뒤에가서 다룬다.

softmax의 Loss function

• MLE를 통해 생각해보자
  여기서는 데이터의 분포가 categorical이다. categorical의 pdf는 아래와 같다.
  

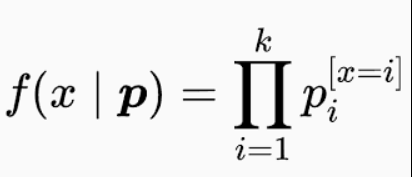
따라서, 이를 NLL로 전개하면 L = $\sum$-log $q_i ^y$가 되고 이를 풀어서 전개하면 $\sum$-$y_i$ log $q_i$이다. 이것이 크로스 엔트로피라 부른다.

이때, L을 가장 최소로 두기위해서는 $\sum$-$y_i$ log $y_i$의 값에 따라가야하는데 이는 항상 0밖에 안나온다. 따라서, 해당 label의 class의 확률 $q_i$로 다가가야 최소가 된다.

즉, sample의 label이 강아지이면 q1이 1 q2,q3가 0으로 가중치를 업데이트 시켜야하는 것이다.

딥러닝 총정리

Step 1 입출력을 정의하고 문제에 따라 이중분류 다중분류 등등을 결정함
Ex) 다중분류

Step 2 Model을 만든다.
Ex) softmax

Step 3 Loss를 정의한다.
Ex) 크로스 엔트로피

Step 4 Weight를 최적화한다.
Ex) Sgd adam 등등

#패스트캠퍼스혁펜하임 #혁펜하임 #혁펜하임AI #패스트캠퍼스 #혁펜하임강의 #AIDEEPDIVE #ai강의 #혁펜하임강의후기