Decision Tree

Decision Tree

Decision Tree Model 소개

나는 개념을 정의할 때 이름과 연관을 지으려고 많이 노력한다. (기억을 자연스레 남기기 위해서) Decision은 결정이고 Tree는 나무이다.

1. 결정 (Decision)
   결정(Decision)의 단어를 보면 어떤 질문에 대해서 결정하는 것으로 생각하자.

2. 나무 (Tree)
   나무(Tree)의 단어를 보면 뿌리를 기반으로 가지를 치고 내려가는 것으로 생각하자.

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

# 붓꽃 데이터 특성 2가지 꽃잎 길이와 너비
iris = load_iris()
X = iris.data[:, 2:] 
y = iris.target

# 위의 데이터로 Decision Tree Model 훈련
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)

# 시각적 표현 
from graphviz import Source
from sklearn.tree import export_graphviz

export_graphviz(
        tree_clf,
        out_file=os.path.join(IMAGES_PATH, "iris_tree.dot"),
        feature_names=iris.feature_names[2:],
        class_names=iris.target_names,
        rounded=True,
        filled=True
    )

Source.from_file(os.path.join(IMAGES_PATH, "iris_tree.dot"))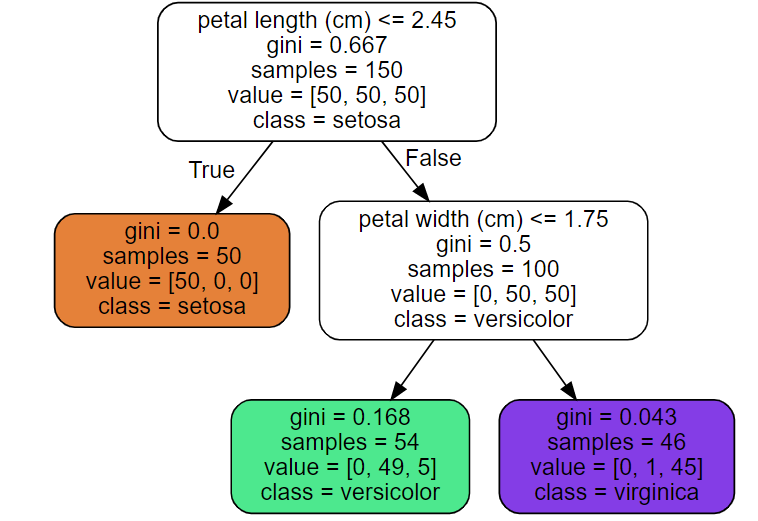

훈련과정의 큰 틀을 살펴보자! 먼저, 데이터를 잘 나눌 수 있는 질문을 선정한다. 이후, Root node(시작 네모박스)에서 질문을 통해 yes, no로 데이터를 나눈다. (군집화 느낌)
이후, 나눈 Node의 불순도를 계산 후 불순도가 더 나아질 수 있으면 질문을 또 선정하여 데이터를 나눈다. 이를 계속 반복하면 leaf node가 여러 개 나온다.

위는 Model의 훈련과정이다. 그리고 이제 predict를 하기위해 새로운 데이터를 넣었을 때 질문을 통해 새로운 데이터는 leaf node를 찾아간다.

1. 분류문제이면 해당 leaf node의 최빈 class(최빈값)을 출력한다.
2. 회귀문제이면 해당 leaf node에 들어있는 data mean(평균값)을 출력한다.

이는 이중분류부터 시작하여 다중분류, 회귀의 분야에서도 사용이 가능하다.

Decision Tree 훈련과정

decision tree는 영역을 두 영역으로 나누는 과정의 반복이다. 그러면 이때, 나눌지 안나눌지 판단을 해야한다. 판단 기준은 크게 2가지가 있다. 1. Entropy, 2. 지니 불순도이다. 하나씩 살펴보자.

Entropy

정보이론에서 나온 개념인 Entropy는 다른 말로 불확실성이다. 간단히 Entropy가 나온 배경에 대해 소개하자면 정보를 처리할 때 데이터의 전달속도 측면을 고려할 때 단어를 전달할 때 비트단위로 전송하게 된다.

이때, 자주 등장하는 단어는 비트를 작게 Set하고 적게 등장하는 단어는 비트를 크게 set하면 데이터를 전달할 때 속도 측면에서 이점을 볼 수 있을 것이다.

• Ex
  case 1) 안녕하세요의 비트수를 100 뷁의 비트수를 0 으로 set
  case 2) 안녕하세요의 비트수를 0 뷁의 비트수를 100 으로 set

이때, 우리는 안녕하세요를 더 많이 쓰니깐 길게 봤을때 case 2가 데이터 전달속도 측면에서 유리할 것이다.

그러면, 이를 구할 때 비트의 길이 수를 기준으로 구하면 된다. 표현식은 $\sum$ $b_i$ $p_i$ ($b_i$는 i번째 단어의 비트 수, $p_i$는 i번째 단어의 등장확률)이다.

근데, 수학적으로 $\sum$ $p_i$ $b_i$ 이 $\sum$ $p_i$ - $log_2 p_i$를 넘을 수 없다. 즉, 하한임이 밝혀졌다. 이 증명은 나중에 다루도록 하자!

그러면, $b_i$ == - $log_2p_i$가 되면 최적의 값이 된다. (즉, 위 예시에서 속도측면에서 강점을 가짐.)

수식적으로 살펴봐도 $p_i$는 양수의 값이고 -$log_2X$의 그래프값은 X가 1($b_i$가 긴 단어)에 다가갈 수록 값이 줄어들고 0($b_i$가 짧은 단어)에 다가갈 수록 기하급수적으로 커지는 것을 보며 단어 Setting을 정할 수 있는 것이다.

entropy 결과값

entropy는 0~1 사이의 값이 가져진다.

1. 엔트로피가 크다 == 불확실성이 크다. (즉, 그 해당 사건에서 뭐가 나올지 예측하기 어렵다.)

2. 엔트로피가 작다 == 불확실성이 작다. (즉, 그 해당 사건에서 뭐가 나올지 예측하기 쉽다.)

예시를 통해 생각해보자. 서로 다른 두 동전이 있다. 한 동전은 앞 뒤가 나올 확률이 같고 한 동전은 앞면밖에 나올 수 없다. 이때, 불확실성이 작은 것은 어느 동전일까??

당연히 앞면밖에 나오지않는 동전이다. 왜냐하면, 시행을 몇번을 하던간에 앞면밖에 나올 수가 없으니 불확실성이 Zero이다. (실제로 식에 넣어봐도 $p_i$가 1이 되므로 log값을 취하면 0이 나와 entropy값이 0이다.)

Decision tree에서는 이정도로만 살펴보고 다음에 크로스 엔트로피 (pi를 몰라서 q로 setting), KL-divergence, mutual information등등에 대해 다뤄보자!

지니 불순도

불순도란? 해당 데이터 집합사이에서 불순물이 얼마나 포함되어 있느냐를 보는 것이다.

$G_i$(지니불순도) = 1 - $\sum$ $p^2$ 이다.

즉, 해당 Node에서 여러 개의 class중에 동일한 class의 데이터들만 포함되어 있을 수록 불순도가 낮다.

지니 불순도 vs Entropy

둘 중 어느 평가지표를 사용해야할지 고민이 될 것이다. 먼저, 속도측면에서는 지니불순도가 높다. (로그의 영향때문에)

하지만, Entropy가 조금 더 균형잡힌 Tree를 만든다.(이유를 잘 모르겠다.)

Decision Tree의 비용함수 (CART Algorithm)

C(k, $t_k$) = ($N_L$ / $N$) $G_L$ + ($N_R$ / $N$) $G_R$ 이다.

($N_L$: 왼쪽 subset의 데이터 수 $N_R$: 오른쪽 subset의 데이터 수, $G_L$: 왼쪽 subset의 지니불순도, $G_R$: 오른쪽 subset의 지니불순도이다.)

식을 자세히 보면 크기에 따라 지니불순도에 가중치가 잡혀있는 것을 확인할 수 있다.
이때, 최소화하는 방식은 cost function이 최소화되는 k, $t_k$의 조합을 찾는 것이다. (k: 특성, $t_k$: 해당 특성의 임계값)

이 과정을 반복해 진행하면 된다.

• 문제점 1
  Algorithm자체가 Greedy하다. 해당 step에서 제일 좋은 곳만 따라가다보니 나무만 바라보고 숲을 못보는 경우가 있다. 즉, 최적해를 100% 보장해주지 않는다.

Decision Tree의 문제점

한 상황을 가정해보겠다.

모든 Leaf Node(분류해주는 Node)가 어떤 방법을 써서라도 지니계수가 0이되면 다 좋은 Decision tree 모델인가??

답은 아니다. 지니계수를 0으로 만들방법은 leaf node를 데이터의 개수만큼 해버린다면 모든 Leaf Node가 0으로 갈 것이다. 그렇다면, 이 Model은 훈련데이터에서는 100 정확한 분류 회귀값을 내지만 실제 데이터를 넣고 predict하면 전혀 관련 없는값이 나올 가능성이 높다. (즉, 데이터에 과대적합된 모델이다.)

따라서, 이러한 것을 제한할 필요가 있다. 그 해결책이 바로 '규제'이다.

Decision Tree의 규제

1. min_samples_split: 분할되기 위해 노드가 가져야 하는 최소 샘플 수
2. min_samples_leaf: 리프 노드가 가지고 있어야 할 최소 샘플 수
3. min_weight_fraction_leaf: min_samples_leaf와 같지만 가중치가 부여된 전체 샘플 수에서의 비율
4. max_leaf_nodes: 리프 노드의 최대 수
5. max_features: 각 노드에서 분할에 사용할 특성의 최대 수

즉, 규제는 과대적합을 막아주는 방법이다.

회귀 (Regression)

위에 살펴본 분류의 과정은 큰틀에서 동일하게 진행된다. 그러면 어느 부분에서 분류와 차이가 날 것같은가?

1. 제일 중요한 Leaf Node에서 값이 class가 아닌 실수값으로 내야하기 때문에 최종 value선택하는 방식이 다를 것이다.

2. 그리고 분류는 클래스를 기반으로 분류하는 반면에 회귀는 값을 실제로 뽑아내야하기 때문에 지니불순도가 아닌 다른 function을 사용할 것이다.

위 1번의 답은 Leaf Node의 평균값으로 값을 가져와 predict해준다. 2번의 답은 보통 MSE를 사용하여 Cost Function을 바꿔준다.

즉, C(k, $t_k$) = ($N_L$ / $N$) $G_L$ + ($N_R$ / $N$) $G_R$ 이것이 아닌 C(k, $t_k$) = ($N_L$ / $N$) $MSE_L$ + ($N_R$ / $N$) $MSE_R$ 이다.

회귀 문제 역시 규제를 통해 과대적합을 피할 수 있다.

Decision Tree의 Pros & Cons

• Pros

1. 매우 구현이 간단하다.
2. 구현 대비 성능이 좋다.

• Cons

1. 과대적합이 되기 쉽다.
2. 결정계가가 수직이라 데이터에 매우 민감하다. (즉, 이 문제점도 과대적합의 문제라고 볼 수 있다. ) 위에 2번 문제에서 데이터가 특히 경계에 있는 값일수록 문제가 더 커진다.
3. 회전에 민감하다. (이것도 데이터 문제)

결론적으로 단점은 데이터에 매우 민감하여 과대적합 및 올바른 학습이 되지 않을 수 있다.