관련 논문 정리
SDE Basic: https://velog.io/@guts4/Generative-Modeling-by-Estimating-Gradients-of-the-Data-Distribution1-Yang-Song-Blog-%EB%A6%AC%EB%B7%B0
SDE 논문리뷰: https://velog.io/@guts4/Generative-Modeling-by-Estimating-Gradients-of-the-Data-Distribution2-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0
DDIM 논문리뷰: https://velog.io/@guts4/Denoising-Diffusion-Implicit-ModelsDDIM-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0

논문의 큰 그림(Conclusion)을 설명한 뒤 논문의 흐름을 그대로 이어서 설명하도록 하겠습니다. 이해가 가지 않은 내용은 대부분 뒤에 다시 한번 언급되기 때문에 막히면 다 읽고 다시 읽는 것을 추천해드립니다.

Conclusion(Summary)

기존에 사용한 Diffusion 모델에 추가 학습 없이 바로 사용할 수 있는 training-free sampling 방식 중에서 DDIM보다 빠른 10 step만에 좋은 결과를 얻을 수 있는 DPM-Solver를 제시했다. linear와 non-linear가 동시에 있는 semi-linearity 부분에서 linear 부분은 analytically compute하고, non-linear 부분은 change of variable 방식을 사용해서 계산을 단순화 시켰습니다. DPM-solver-1,2,3이 존재하고 higher-order일수록 더 좋은 결과를 나타냅니다. Scheduler의 경우, SNR을 기반으로한 uniform한 방식과 adaptive step size를 제시했습니다.

Introduction

Diffusion probabilistic models(DPMs)는 많은 분야에서 좋은 성과를 냈습니다. DPMs는 단절된 시간을 사용하는 방법과, 연속적인 시간을 사용하는 SDE 방식으로 나눠집니다. GAN과 VAE에 비해서 좋은 샘플링 결과와 정확한 likelihood 를 계산할 수 있다는 장점이 있지만 좋은 결과를 얻기 위한 샘플링 속도는 오래걸린다는 한계점이 존재합니다.

기존에 존재하는 DPM에 관한 fast samplers는 knowledge distillation 방법과 noise level or sample trajectory learning이 있습니다. 2가지 방법은 효율적인 샘플링 이전에 많은 훈련이 필요하고, applicability와 flexibility가 제한적입니다.

다음으로 Training-free samplers가 존재하긴하지만 해당 방식들도 여전히 좋은 퀄리티의 샘플을 얻기위해서는 시간이 소요된다는 한계점이 존재합니다.

이 논문에서는 10step이내에 좋은 퀄리티의 샘플을 얻을 수 있는 방법을 제시했습니다. 기존에 ODE를 DPMs에 적용한 방법은 linear와 non-linear한 부분 모두를 ODE Solver를 통해서 해결했습니다. 이 방법에 의문을 제기하고 linear 방식은 analytically compute한게 해당 논문의 contribution입니다. 또한, Change-of-variable을 통해 ODE의 해를 Exponentially Weighted Integral 형태로 변환하여 효율적인 근사가 가능하게 했습니다.

위에서 설명한 방식의 이름은 DPM-Solver이고 이는 contionus와 discrete한 방법 모두에 적용 가능하고 또한 classifier guidance도 적용할 수 있습니다.

위의 사진은 DDIM에 비해서 적은수의 NFE(number of function evaluations)로도 더 좋은 결괄르 보이는 것을 알 수 있습니다.

Diffusion Probabilistic Models

Forward Process and Diffusion SDEs

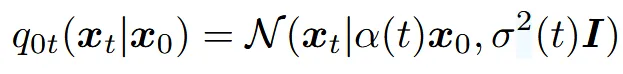
우리가 모르는 데이터 분포 $x_0$에 대해서 0과 T시점 사이의 t시점에서의 데이터의 분포는 위와 같이 나타낼 수 있습니다. $a_t$와 $\sigma_t$는 DPM의 noise schedule입니다. singal-to-noise-ratio(SNR)은 $α^2_t/σ^2_t$로 나타낼 수 있고 이 비율은 점점 감소하게됩니다. 즉 time step이 커질수록 추가되는 노이즈의 양이 많아지게 됩니다.

추가적으로 stochastic differential equation(SDEs)는 Diffusion 모델과 같은 전이 방법을 사용한다고 합니다.

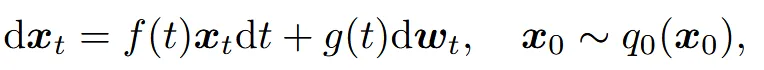
SDE는 위와 같은 항으로 나타내는데, 이때 f(t)는 drift 항, g(t)는 diffusion 항이고 $w_t$는 Wiener process로서 노이즈가 추가되는 부분입니다. 자세한 내용은 위에 나와있던 SDE 논문리뷰를 참고하시면 도움이 되실겁니다.

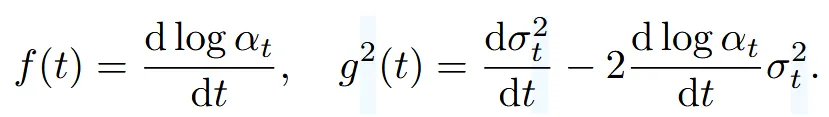
f(t)와 $g^2(t)$는 위와 같이 나타낼 수 있습니다. 위의 수식 전개과정은 “Variational diffusion models”을 참고하시면됩니다.

결론적으로 위와 같은 수식을 SDE로부터 얻을 수 있고, 위의 식에서 우리가 모르는 값은 score function을 나타내는 $∇_x log q_t(x_t)$밖에 없습니다.

Score function은 노이즈를 예측하는 파라미터 $\epsilon_{\theta}$를 학습하면서 예측하게됩니다. 학습할 때 위의 Loss function을 최소화하면서 학습하게 됩니다.

최종적으로 위의 수식에서 노이즈를 예측하는 방식으로 SDE를 풀게되는데, 이 방식은 매우 느린 샘플링 속도를 갖고 있습니다.

Diffusion (Probability Flow) ODEs

SDE의 경우 Wiener process의 랜덤성 때문에 step size가 충분히 커야합니다. 하지만 큰 step size는 non-converence를 야기합니다. 이러한 문제점을 해결하고자 probability flow ODE라는 논문이 나왔습니다. 해당 논문에서 ODE와 SDE의 Marginal distribution은 동일하가도 했습니다.

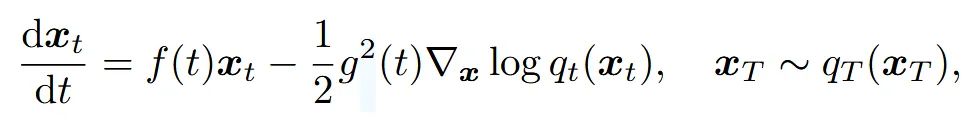
t시점에서 SDE와 동일한 marginal distribution을 갖는 ODE를 probability flow ODE라고 명명했고, score function을 noise prediction model의 형태로 바꿀경우 아래와 같이 나타납니다.

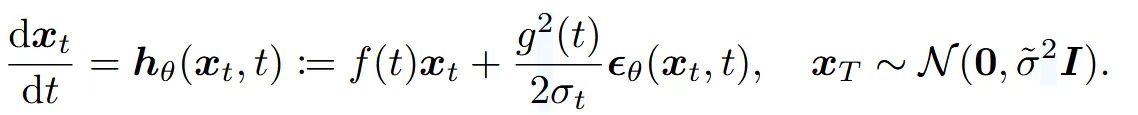
SDE와 비교해서 ODE는 랜덤성이 없기 때문에 step size의 제한이 없습니다. 게다가 SDE는 Δt가 랜덤성때문에 작은 수로 제한되지만, 랜덤성이 제거된 ODE의 경우 Δt가 커도 괜찮습니다.. Δt가 클 경우 더 적은 수의 time step으로 샘플링이 가능하기 때문에 샘플링 시간을 단축 시킬 수 있습니다. 결론적으로 SDE는 1000 step이 필요하지만, ODE는 RK45 ODE solver를 이용해서 60step으로도 좋은 결과를 낼 수 있습니다. 하지만 10step처럼 극단적으로 작은 step으로는 좋은 결과를 낼 수 없습ㄴ디ㅏ.

Customized Fast Solvers for Diffusion ODEs

Simplified Formulation of Exact Solutions of Diffusion ODEs

첫번재 핵심 아이디어는 선형과 비선형 방식을 분리해서 각각 진행하는 것입니다.

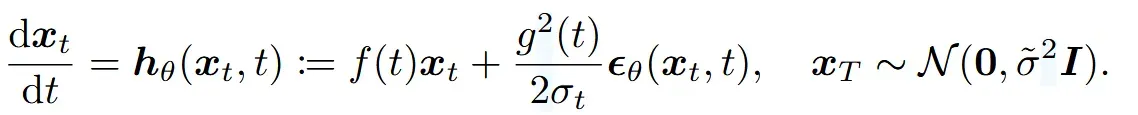
위의 수식에서 첫번째 항 $f(t)x_t$부분은 linear function 두번째 항 $\frac{g^2(t)}{2\sigma_t}$은 non-linear한 부분입니다. 기존 probabilirt flow ODE에서는 $h_θ(x_t,t)$를 이용해서 두가지 항을 동시에 예측하도록 해서 linear와 non-linear 두가지 항 모두에서 discretization error를 야기했습니다.

linear와 non-linear를 분리하기 위해서 variation of constants 공식을 사용했습니다.

variation of constants 공식을 적용한 결과는 위와같습니다. linear와 non-linear부분을 분리함으로서 linear 부분은 approximation error를 제거하면서 계산할 수 있는 형태로 나타낼 수 있습니다. 하지만 여전히 non-linear 부분의 경우 f(r), g(r), $σ_r$과 복잡한 neural network $\epsilon_{\theta}$로 나타나 있어서 매우 복잡합니다.

두번째 핵심 아이디어는 non-linear 부분의 적분을 간소화하는 것입니다.

우선 $λ_t$(= $log(a_t/\sigma_t$))라는 log-SNR의 절반을 나타내는 변수를 도입합니다.

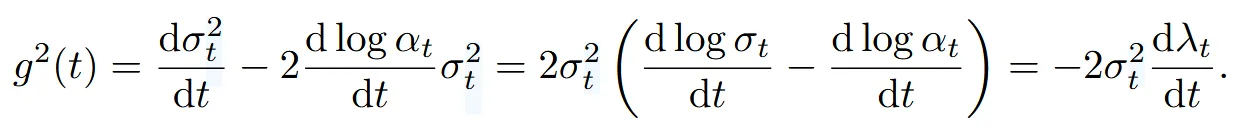
$λ_t$는 SNR로서 시간이 증가할수록 감소하게됩니다. 해당 변수를 이용해서 $g^2(t)$를 나타내면 위와 같이 간소화할 수 있습니다. SDE 수식 f (t) = d log αt/dt 값과 위에서 구한 $g^2(t)$를 $λ_t$로 변환한 식을 대입하면 아래와 같은 최종식을 얻을 수 있습니다.

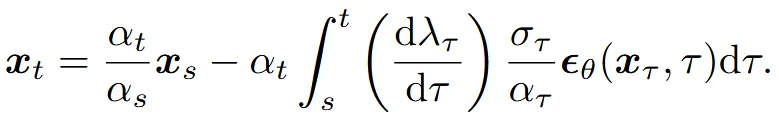
더 나아가서 위의 수식에서 x의 아래첨자 t를 λ로 변환해서 $\theta$와 t의 복잡도를 줄이도록 했습니다. 2 변수의 복잡도가 높은 이유는 $\theta$는 시간(t)에 따라 scale변화와 노이즈가 추가되는 정도를 모두 고려해야되기 때문입니다. 반면에 λ의 경우 sclae과 노이즈가 추가되는 정도가 변수로 지정되어 있기때문에 복잡도가 줄어들게 됩니다.

$\hat{x}_{\lambda} := x_{t_\lambda(\lambda)}$를 change-of-variable 공식을 이용해서 대입하게 되면 최종적으로 위와 같은 수식을 얻을 수 있습니다. 뒤의 적분 부분을 $\hat{\epsilon}_{\theta}$의 exponentially weighted integral라고 명명했습니다.

결론적으로, 선형 부분은 해석적으로 정확한 값을 구할 수 있고, 비선형 부분은 $\lambda_t$의 도입과 시간t를 λ로 변환함으로써 복잡성이 단순화되어 오차를 줄이고 더 빠르고 안정적인 계산이 가능해졌습니다.

High-Order Solvers for Diffusion ODEs

해당 부분에서 많은 수학적 요소들의 설명이 나옵니다. 최대한 수학적인 요소들을 배제한 설명을 하도록 하겠습니다. 한마디로 설명하면 고차 Diffusion ODE Solver는 Exponentially Weighted Integral을 Taylor 전개로 근사하고 Integration-by-Parts로 적분을 해석적으로 계산함으로써 정확도와 효율성을 동시에 달성합니다.

T부터 M까지 M+1개의 time steps들에 대해서 $t_0$=T, $t_M$=0으로 나타냅니다. 제안된 solver는 $\tilde{x}_{t_i}$로 나타냅니다. 마지막 값을 나타내는 $\tilde{x}_{t_M}$는 시간 0에서의 추정된 값입니다. 추정 오차를 줄이기 위해서는 각각의 step에서 $\tilde{x}_{t_i}$를 줄일 필요가 있습니다. $t_{i-1}$에서 $t_i$로의 변환은 아래와 같은 수식으로 나타낼 수 있습니다.

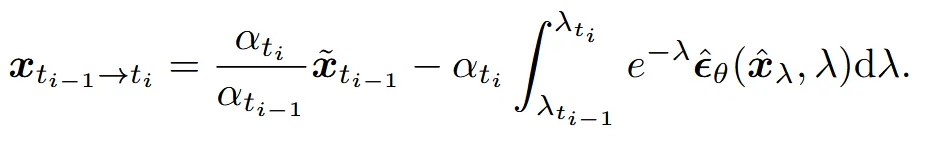
해당 수식은 이전의 수식에서 t대신 $t_i$ s대신 $t_{i-1}$을 대입해서 나온 결과입니다. Exponentially weighted integral의 항은 단순화 한 항이지만 여전히 계산하기엔 복잡합니다. 따라서 Taylor expansion을 이용해서 이를 더 단순화 했습니다.

위의 식은 $\epsilon_{\theta}$에 대한 k-1차 Taylor 급수 방정식입니다. 이를 이전의 $t_i$ → $t_{i+1}$로 변환한 수식에 대입하면 최종적으로 아래의 수식을 얻게됩니다.

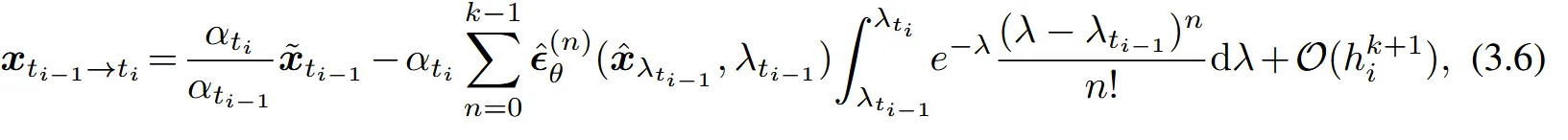
위의 수식에서의 적분을 n번 반복하게 되면 linear 부분과 동일하게 analytically 계산이 가능하게 됩니다. 자세한 내용은 Appendix B.2를 참고하시면됩니다. 이후 stiff order conditions를 통해 안정성을 보장하여 k-차 정확도를 가진 DPM-Solver-K를 정의했습니다. k=1일 때의 식은 아래와 같습니다.

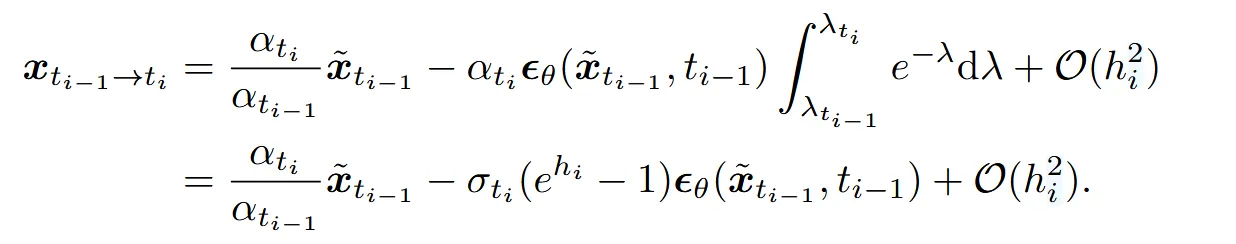
k가 2보다 크거나 같을 때 t와 s사이의 추가적인 Taylor expansion이 필요합니다. 해당 내용은 Appendix B 에 나와있고 k가 2와 3일 때 알고리즘은 아래와 같이 나타나있습니다.

우선 k=2인 DPM-Solver-2부터 알아보도록 하겠습니다. 핵심 내용은 중간에 $u_i$라는 중간 항을 거치는 것입니다. 참고로 3번째 줄에 나타난 $t_λ$ 값은 λ(t)의 역함수입니다.

첫번째로 i와 i-1의 $λ_t$의 값의 중간값인 $s_i$를 3번째 줄에서 구합니다. 이후 중간값인 $u_i$를 i와 i-1의 중간 시간 값($h_i/2$)으로 나타냅니다. 5번째 줄에서는 중간값을 이용해서 노이즈를 예측하고 최종적으로 i시점의 값을 예측하게 됩니다. 이때 hi가 절반이 아닌 원래의 값을 이용한 이유는 노이즈의 예측만 중간 시점에서 한 것이지 앞의 $\tilde{x}_{t_{i-1}}$를 사용해서 i시점을 예측했기 때문에 시간 간격은 $h_i$를 그대로 사용해야됩니다.

다음으로 k=3인 DPM-Solver-3에 대해서 알아보도록 하겠습니다. 핵심 내용은 이전에서 중간 항이 1개였던거를 2개로 변경한 것입니다.

큰 틀은 비슷하지만 첫번째 중간값인 $D_{2i-1}$과 두번째 중간값인 $D_{2i}$, 즉 2개의 중갑값이라는 점과 6번째, 8번째 줄의 코드를 보면 첫번째 중간단계의 오차를 반영하는 식만 추가된 것을 확인할 수 있습니다.

알고리즘 2,3을 통해서 봤던 것처럼 DPM-Solver-k는 k개의 function이 필요하고, k-1개의 중간값이 필요합니다.

Theorem 3.2에서는 DPM-Solver-k가 Diffusion ODE의 k-차 Solver와 동일한 역할을 수행하는 것을 입증했습니다. 자세한 내용은 Appendix를 참고하시면 되고, 차수가 높을수록 더 높은 정확도를 달성함을 보장합니다. 결론적으로 이 논문에서 linear 부분을 해석적으로 풀고, non-linear 부분을 단순화해도 Theorem 3.2를 통해서 Diffusion ODE Solver와 동일한 역할을 하는 것을 알 수 있습니다.

Step Size Schedule

위에서 사용한 solver들은 사전에 time steps들을 정의할 필요가 있었습니다. 따라서 2가지 time steps들을 정의할 schedule을 제시했습니다. 첫번째로 동일한 간격을 갖는 방법입니다. 이때 단순히 시간을 기준으로 동일한 간격을 찾는 것이 아닌, SNR을 나타내는 λ값을 기준으로 균등하게 분할합니다.

두번째 방법은 adaptive step size 알고리즘을 적용하는 방식입니다. 이는 서로다른 DPM-Solver를 결합해서 step size를 수정하는 방식입니다. 자세한 내용은 Appendix를 참고하시면 됩니다.

Adaptive step size를 적용할 때 NFE(Number of Function Evaludations)의 개수가 3으로 나눠지지 않은 경우는 DPM-Solver-3을 사용할 수 없습니다. 왜냐하면 time step = NFE / k인데 time step은 정수의 값을 가져야 되기 때문입니다. 따라서 3으로 나눈 나머지가 2인 경우 DPM-Solver-2, 1인 경우 DPM-Solver-1을 사용하게 됩니다. NFE가 20 이하일 경우는 uniform 방식을, 이외에는 Adaptive step size를 적용했습니다.

Sampling from Discrete-Time DPMs

Discrete-time DPM은 고정된 N개의 time steps으로 나누어지고, 각 단계에서 노이즈의 예측을 진행하게 됩니다.

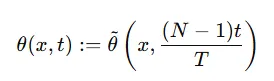
이를 Continuous-time DPM으로 바꿀경우 왼쪽의 Discrete한 식에서 오른쪽 Continuous한 식으로 바꿔야 합니다. Discrete한 경우 0~N까지 총 N-1개의 경우의 수가 있고 Continuous time t를 Dicsret 시간 단계 n으로 변환하기 위해서 (N-1)t / T를 사용합니다. Smoothe Time Embedding 덕분에 Time step이 정수가 아니어도 잘 작동하게 됩니다.

Comparison with Existing Fast Sampling Methods

기존에 존재하는 ODE 기반 모델들과의 비교를 진행할 것이고, 추가적으로 training-free 모델이 training-base 모델에 비해서 가지는 이점에 대해서 설명할 것 입니다.

DDIM as DPM-Solver-1

DDIM은 DPMs를 determinisitic하게 바꿔서 빠른 sampling을 가능하게 한 방법입니다.

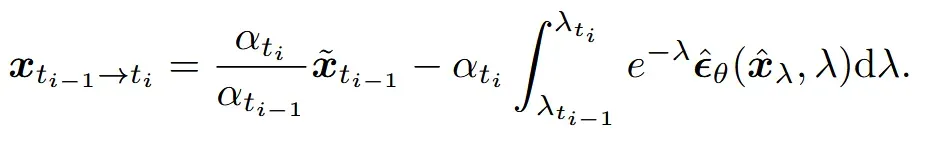
위의 DPM-Solver-1에서 적분에 나온 λ변수만 log와 e를 빼고 SNR형태로 나타내면 아래와 같이 나타낼 수 있습니다.

이 형태는 DDIM과 똑같은 방식으로 진행됩니다. 하지만 DPM-Solver는 더 높은 order로 풀 수 있습니다. 다른 논문에서도 DDIM이 1차 Diffusion ODE와 동일하다고 설명했지만 이유를 밝히진 못 했습니다. 하지만 이 논문에서는 DDIM이 DPM-Solver의 특별한 경우인 것을 나타냈습니다.

Comparison with Traditional Runge-Kutta Methods

High-order solver중 하나인 Runge-Kutta(RK) 방법을 이용해서 diffusion ODE를 푼 경우가 있습니다.

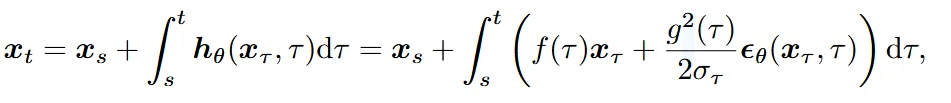
Time step [t,s]에서 $h_{\theta}$를 적분을 이용해서 구하는 방법입니다. 이때의 Error는 $h_{\theta}$ 값에 의해서 결정되고, 이는 다시 linear 부분인 $f(r)x_r$과 non-linear 부분인 $\epsilon_{\theta}$에 의해서 구해집니다. Linear 부분은 위에서 $e^{\int_{t}^{s} f(\tau) d\tau}$라고 정의했고, 이 수식에 따르면 error가 시간이 지날수록 지수차만큼 증가하게 됩니다. 따라서 큰 시간 간격을 사용할 경우 RK 방법의 오차가 증가해 불안정합니다.

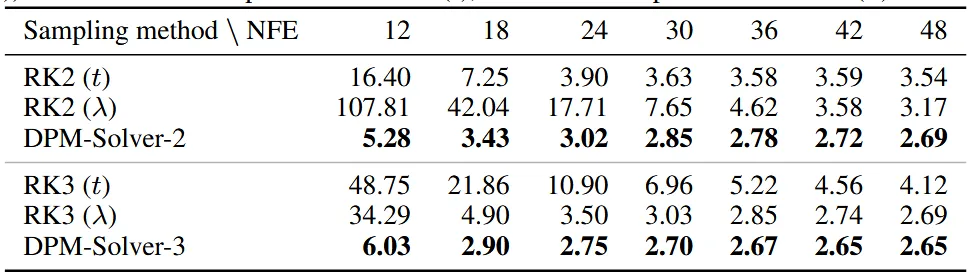
위에서 설명한 RK방법과 DPM-Solver 방법을 동일 차에서 비교한 결과입니다. CIFAR-10데이터를 기준으로 다양한 number of function evaluations(NFE)의 값에 따른 FID 값을 나타낸 것입니다. RK2 다음에 나타난 t와 $\lambda$는 uniform time step을 time step기준으로 할지, 아니면 SNR 값을 기준으로 할지를 나타낸 것입니다. 결론적으로 DPM-Solver가 RK보다 성능이 좋고, 당연히 NFE가 증가할수록 성능이 좋음을 나타냈습니다. 특이한 점은 2차에서는 time step을 time으로 동일하게 나눈 수치가 SNR을 기준으로 나눈 수치보다 좋게 나왔지만, 3차에서는 반대로 나왔습니다.

Training-based Fast Sampling Methods for DPMs

DPM의 느린 샘플링 문제를 해결하기 위한 다양한 접근법들이 나왔습니다. Training-Based Samplers는 추가 학습이나 최적화가 필요하지만, Training-Free Samplers는 기존 DPM 모델을 그대로 사용하여 더 유연하게 동작할 수 있습니다. Training-Free Samplers는 원본 DPM 모델의 정보를 손실 없이 유지하면서도 조건부 샘플링과 같은 다양한 확장에 더 적합합니다.

또한 Fast Sampling이라는 새로운 관점의 논문들도 나왔는데, 해당 논문에 DPM-Solver를 쉽게 적용 가능할 것으로 보이고, 이는 Future Works로 냅뒀습니다.

Experiments

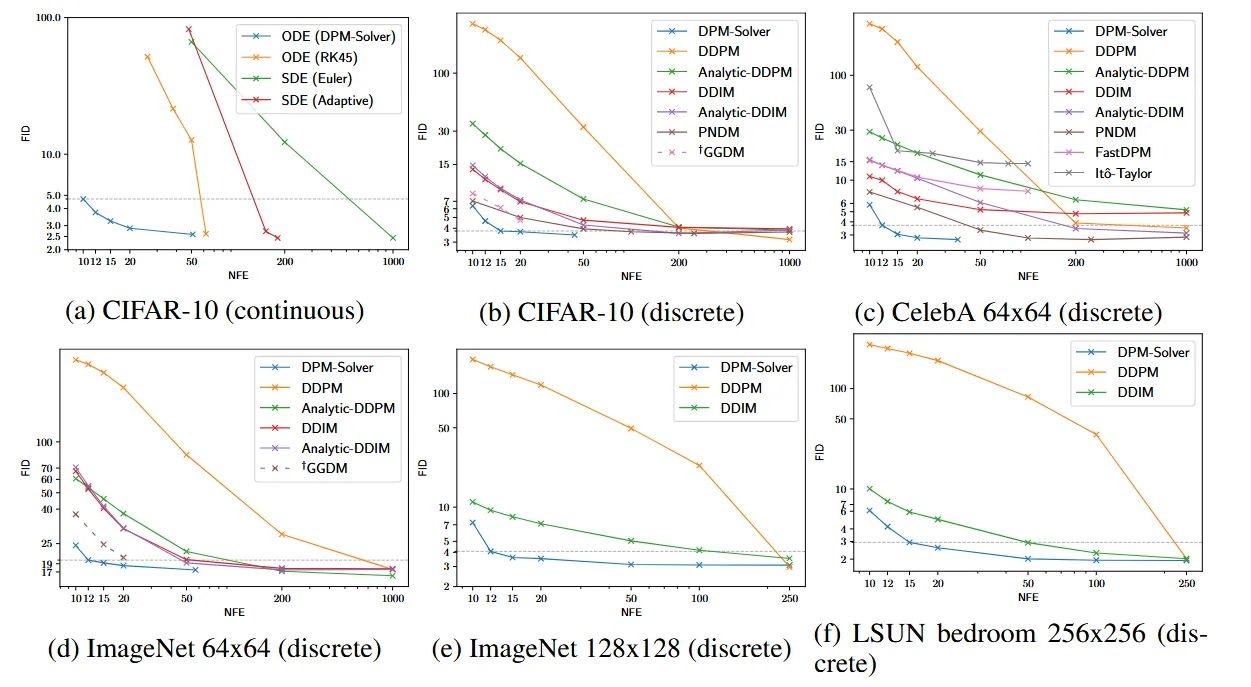
DPM-Solver를 continuous한 경우와 discrete한 경우 모든 경우에 대입해서 실험할 것이고, 스케줄러는 이전에 말한것처럼 20보다 작은 경우는 uniform하게, 큰 경우는 adaptive step size를 이용하도록 설정했습니다. 실험결과는 FID score를 기반으로 비교합니다.

Comparison with Continuous-Time Sampling Methods

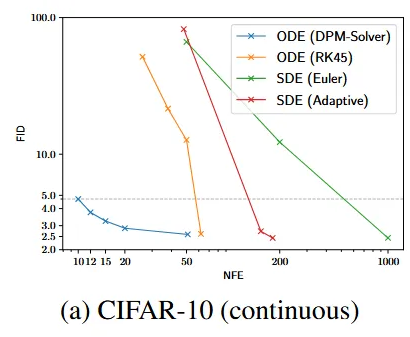
첫번째로 continuous-time sampling 방법에 대해서 비교해 보겠습니다. Diffusion SDE쪽에서 Euler-Maruyama를 사용한 방법과, adaptive step size를 적용한 방법에 대해서, Diffusion ODE쪽에서는 RK 모델에 대해서 비교했습니다. 이 모델들을 “VP deep”으로 사전학습된 모델을 기반으로 CIFAR-10 데이터셋을 샘플링하게 됩니다. Adaptive SDE의 경우 uniform한 time step과 함께 50,200,1000개의 NFE의 결과를 얻었고, Adaptive SDE의 경우 시간 간격을 상황에 따라 동적으로 조정했습니다. RK45 ODE의 경우 4차와 5차 Runge-Kutta 방법을 사용해서 adaptive step size를 사용하여 더 효율적인 계산을 하도록 설정했습니다. 결론을 본다면 NFE가 10일 때 DPM-Solver가 FID score가 약 5를 달성한 것으로 다른 모델들에 비해서 5배 이상 빠른 결과를 얻었습니다.

여기서 사용한 DPM-Solver의 k차가 몇인지는 안나와있으나, 아래의 추가적인 설명(2차와 3차 결과도 있다)을 기반으로 k=1일 것이다고 추정할 수 있습니다.

Comparison with Discrete-Time Sampling Methods

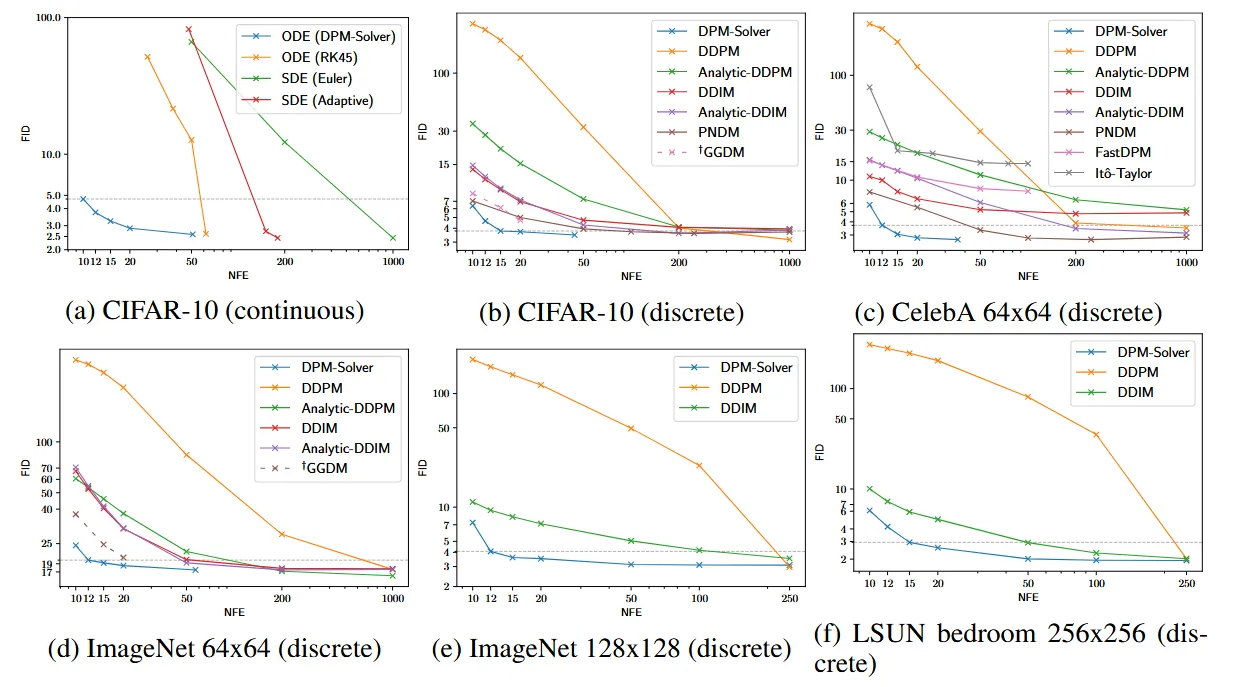
DPM-Solver를 discrete-time DPMs에 적용해서 DDPM, DDIM, Analytic-DDPM, Analytic-DDIM, PNDM, FastDPM, Ito-Taylor와 같은 다양한 모델들과 비교했습니다. 추가적으로 training-based samplers의 GGDM과의 비교도 진행했습니다. NFE는 10부터 1000까지 변형했습니다. 다양한 데이터들에서 DPM-Solver의 결과를 확인할 수 있고, 심지어 training-based samplers인 GGDM의 성능보다 더 높은 것을 확인할 수 있습니다.

Conclusion

기존에 사용한 Diffusion 모델에 추가 학습 없이 바로 사용할 수 있는 training-free sampling 방식 중에서 DDIM보다 빠른 10 step만에 좋은 결과를 얻을 수 있는 DPM-Solver를 제시했다. linear와 non-linear가 동시에 있는 semi-linearity 부분에서 linear 부분은 analytically compute하고, non-linear 부분은 change of variable 방식을 사용해서 계산을 단순화 시켰습니다. DPM-solver-1,2,3이 존재하고 higher-order일수록 더 좋은 결과를 나타냅니다. Scheduler의 경우, SNR을 기반으로한 uniform한 방식과 adaptive step size를 제시했습니다.

Limitations

물론 빠른 Sampling 속도라는 점을 제시했지만, likelihood evaluations 방법으로는 적절하지 않습니다. 추가적으로 가짜 이미지 생성으로 악용될 가능성이 있습니다.