선형 회귀 분석
1. 모델 파라미터 변화 표현하기
import csv
import matplotlib.pyplot as plt
from math import isclose
# Linear Model
def f(theta0, theta1, theta2, theta3, x, y, z):
return theta0 + theta1 * x + theta2 * y + theta3 * z
# Objective Function
def J(theta0, theta1, theta2, theta3, points):
sigma = 0
for point in points:
sigma += (f(theta0, theta1, theta2, theta3, point[0], point[1], point[2]) - point[3]) ** 2
return (1 / (2 * len(points))) * sigma
# Derivative of Objective Function by theta_i
def dJ_dtheta_i(theta0, theta1, theta2, theta3, points, i):
sigma = 0
for point in points:
if(i is 0):
sigma += (f(theta0, theta1, theta2, theta3, point[0], point[1], point[2]) - point[3])
else:
sigma += (f(theta0, theta1, theta2, theta3, point[0], point[1], point[2]) - point[3]) * point[i - 1]
return (1 / len(points)) * sigma
# training data set
train_set = []
# load training data set
with open('drive/My Drive/.../data_train.csv', newline='') as myfile:
reader = csv.reader(myfile, delimiter=',')
for i in reader:
train_set.append([float(i[0]), float(i[1]), float(i[2]), float(i[3])])
# the initial condition
theta0 = 1
theta1 = 1
theta2 = 1
theta3 = 1
learning_rate = 0.00002
theta0_i = []
theta1_i = []
theta2_i = []
theta3_i = []
while(1):
# plot the estimated parameters {(θ0, θ1, θ2, θ3)} at every iteration of gradient descent
theta0_i.append(theta0)
theta1_i.append(theta1)
theta2_i.append(theta2)
theta3_i.append(theta3)
# the optimization is performed using the training dataset ('data_train.csv')
next_theta0 = theta0 - learning_rate * dJ_dtheta_i(theta0, theta1, theta2, theta3, train_set, 0)
next_theta1 = theta1 - learning_rate * dJ_dtheta_i(theta0, theta1, theta2, theta3, train_set, 1)
next_theta2 = theta2 - learning_rate * dJ_dtheta_i(theta0, theta1, theta2, theta3, train_set, 2)
next_theta3 = theta3 - learning_rate * dJ_dtheta_i(theta0, theta1, theta2, theta3, train_set, 3)
# the gradient descent is performed until the convergence of (θ0, θ1, θ2, θ3) is achieved
if(isclose(next_theta0, theta0) and isclose(next_theta1, theta1) and isclose(next_theta2, theta2) and isclose(next_theta3, theta3)):
break
# update {(θ0, θ1, θ2, θ3)}
theta0 = next_theta0
theta1 = next_theta1
theta2 = next_theta2
theta3 = next_theta3
print(len(theta0_i), theta0, theta1, theta2, theta3, J(theta0, theta1, theta2, theta3, train_set))
# the colors for the parameters (θ0, θ1, θ2, θ3) is black, red, green, blue, respectively
plt.figure(figsize=(8, 8))
plt.plot(range(len(theta0_i)), theta0_i, color='black')
plt.plot(range(len(theta1_i)), theta1_i, color='red')
plt.plot(range(len(theta2_i)), theta2_i, color='green')
plt.plot(range(len(theta3_i)), theta3_i, color='blue')
plt.show()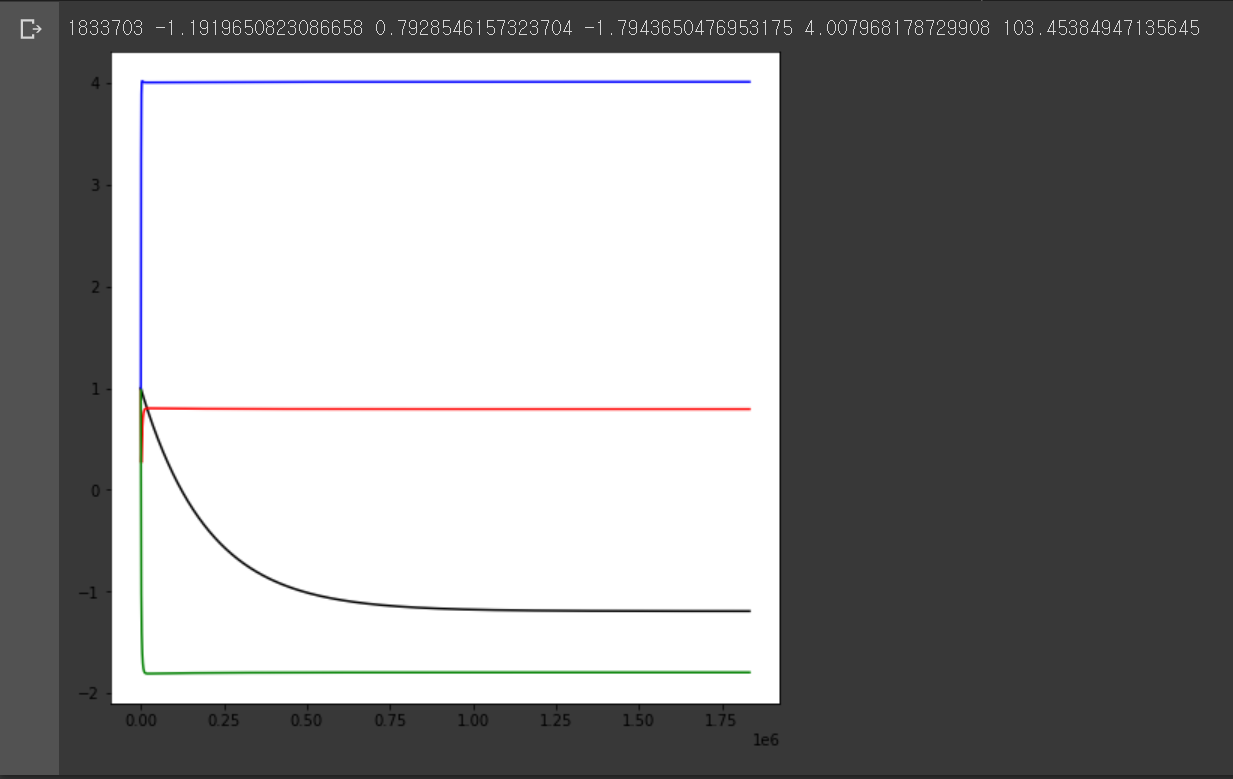
데이터 셋이 3차원 이상일 때도 위와 같이 경사하강법을 통해 선형 회귀 분석을 할 수 있다. 위 그래프는 경사하강법 각 단계에 따른 의 변화 과정을 나타낸 것이다. 의 그래프 색은 각각 검정, 빨강, 초록, 파랑이다. 을 제외한 나머지 변수는 빠르게 특정 값에 수렴된 것을 볼 수 있다.
경사하강법으로 변수가 여러 개인 선형 회귀 분석을 하는 과정은 아래와 같다.
-
4차원의(변수 4개) 데이터 셋을 불러온다. 는 입력값이고, 는 기대되는 출력값이다.
-
선형 함수(1차 함수)를 설정한다.
, -
목적 함수(에러 함수)를 설정한다. 우리는 이 목적 함수가 최소가 되게 하는 , , , 을 구하려고 한다.
, -
경사하강법(Gradient Descent)으로 목적 함수의 값이 최소가 되는 지점의 , , , 을 찾아간다. 값은 너무 크면 값이 발산하고, 너무 작으면 수렴하지만 계산이 오래 걸리기 때문에 적절한 값으로 설정한다.
,
,
,
,
-
경사하강법의 매 단계마다 값을 저장해 그래프로 그린다.
2. 오차 함수 변화 표현하기
import csv
import matplotlib.pyplot as plt
from math import isclose
# Linear Model
def f(theta0, theta1, theta2, theta3, x, y, z):
return theta0 + theta1 * x + theta2 * y + theta3 * z
# Objective Function
def J(theta0, theta1, theta2, theta3, points):
sigma = 0
for point in points:
sigma += (f(theta0, theta1, theta2, theta3, point[0], point[1], point[2]) - point[3]) ** 2
return (1 / (2 * len(points))) * sigma
# Derivative of Objective Function by theta_i
def dJ_dtheta_i(theta0, theta1, theta2, theta3, points, i):
sigma = 0
for point in points:
if(i is 0):
sigma += (f(theta0, theta1, theta2, theta3, point[0], point[1], point[2]) - point[3])
else:
sigma += (f(theta0, theta1, theta2, theta3, point[0], point[1], point[2]) - point[3]) * point[i - 1]
return (1 / len(points)) * sigma
# training data set
train_set = []
# load training data set
with open('drive/My Drive/.../data_train.csv', newline='') as myfile:
reader = csv.reader(myfile, delimiter=',')
for i in reader:
train_set.append([float(i[0]), float(i[1]), float(i[2]), float(i[3])])
# the initial condition
theta0 = 1
theta1 = 1
theta2 = 1
theta3 = 1
learning_rate = 0.00002
J_i = []
while(1):
# plot the objective function at every iteration of gradient descent
J_i.append(J(theta0, theta1, theta2, theta3, train_set))
# the optimization is performed using the training dataset ('data_train.csv')
next_theta0 = theta0 - learning_rate * dJ_dtheta_i(theta0, theta1, theta2, theta3, train_set, 0)
next_theta1 = theta1 - learning_rate * dJ_dtheta_i(theta0, theta1, theta2, theta3, train_set, 1)
next_theta2 = theta2 - learning_rate * dJ_dtheta_i(theta0, theta1, theta2, theta3, train_set, 2)
next_theta3 = theta3 - learning_rate * dJ_dtheta_i(theta0, theta1, theta2, theta3, train_set, 3)
# the gradient descent is performed until the convergence of (θ0, θ1, θ2, θ3) is achieved
if(isclose(next_theta0, theta0) and isclose(next_theta1, theta1) and isclose(next_theta2, theta2) and isclose(next_theta3, theta3)):
break
# update {(θ0, θ1, θ2, θ3)}
theta0 = next_theta0
theta1 = next_theta1
theta2 = next_theta2
theta3 = next_theta3
# debug
print('Step count:', len(J_i))
print('Theta0:', theta0)
print('Theta1:', theta1)
print('Theta2:', theta2)
print('Theta3:', theta3)
print('J(t0, t1, t2, t3) with traning data:', J(train_set, theta0, theta1, theta2, theta3))
# plot the training error J(θ0, θ1, θ2, θ3) at every iteration of gradient descent until convergence (in blue color)
plt.figure(figsize=(8, 8))
plt.plot(range(len(J_i)), J_i, color='blue')
plt.show()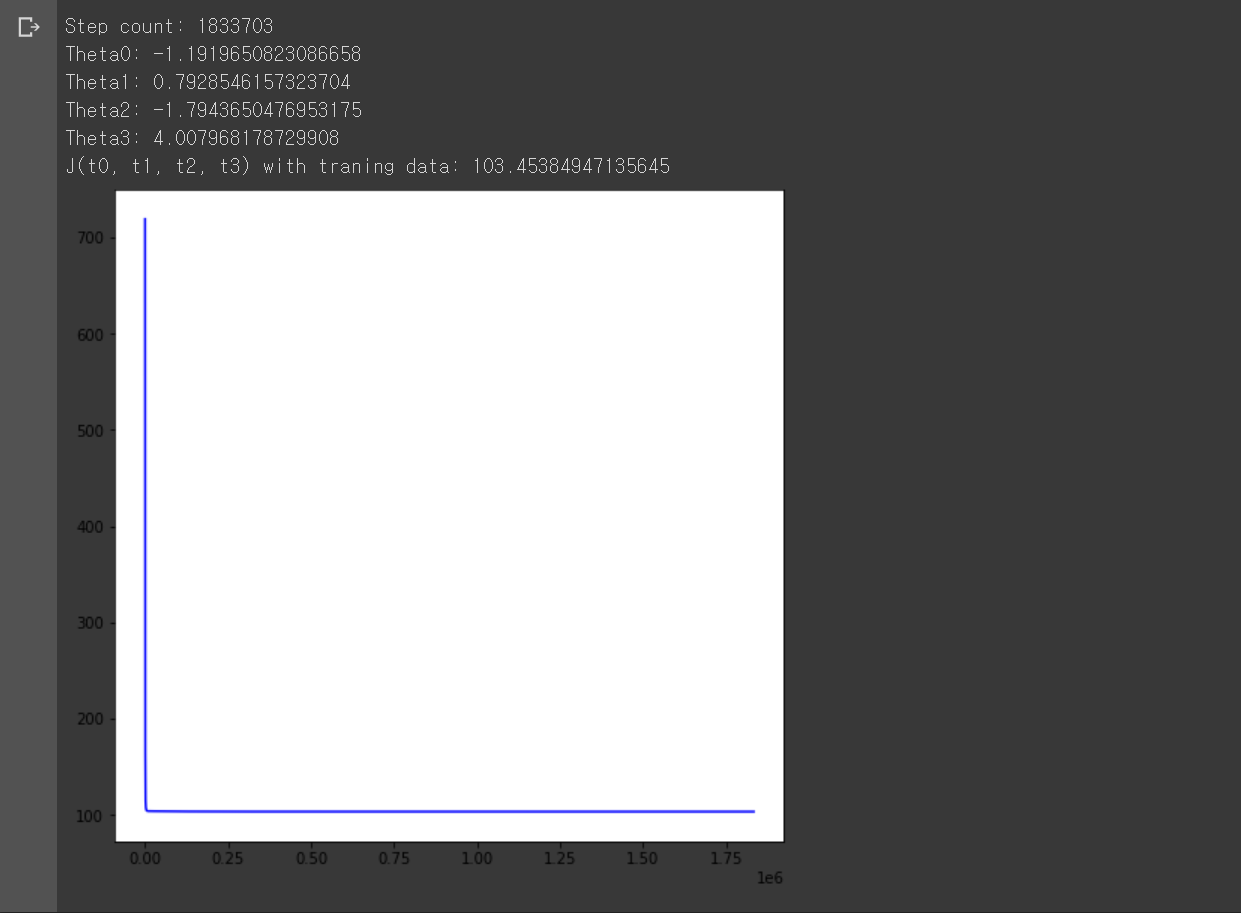
위 코드랑 거의 동일하고, 출력 그래프만 매 경사하강법 단계마다 목적 함수가 어떻게 변경되는지로 변경됐다. 목적 함수가 수렴하는 것에 비해 반복 횟수가 너무 많아 그래프의 변화가 잘 보이지 않는다.
