https://ratsgo.github.io/speechbook/docs/am 이 홈페이지를 참고해서 공부 !!한 내용들을 간단하게 적어보려고 한다
여기는 음향 모델(Acoustic Model) 관련 부분이다.
1. Hidden Markov Model
2. Baum-Welch Algorithm
상태, 관측치를 모두 아는 경우 -> 은닉마코프모델을 학습하기가 상대적으로 쉽다 (개수 세면 끝)
3. Gaussian Mixture Model
3.1 Univariate Normal Distribution
정규분포 = 가우스 분포
수식
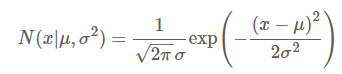
단변량 정규분포는 파라미터 μ, σ가 두 개로, 그에 따라 분포가 바뀜
3.2 Multivariate Normal Distributution
입력 변수가 D 차원인 벡터 -> 다변량 정규분포(Multivariate Normal Distributution)
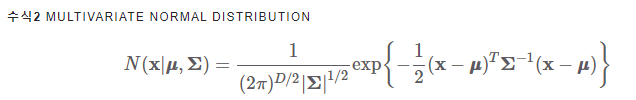
μ : D차원의 평균 벡터
Σ: D * D 크기를 가지는 공분산 행렬
|Σ|: Σ의 행렬식
2차원 다변량 정규분포는 평균, 공분산 등에 따라 -> 분포가 바뀜
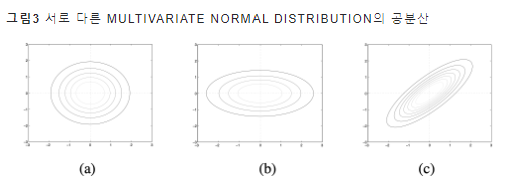
서로 다른 공분산을 가진 세 개의 2차원( X , Y ) 다변량 정규분포를 나타낸 것
세로(X), 가로 (Y)
(a) 공분산 행렬이 [[1, 0], [0, 1]] -> 대각성분 이외의 요소값이 0인 대각행렬(diagonal matrix)이며 대각성분의 모든 값이 1로 동일
X 와 Y의 분산이 1, 둘의 공분산은 0이라는 뜻 -> contour plot이 원형으로 나타남
(b) 공분산 행렬이 [[0.6, 0], [0, 2]] -> X 의 분산은 0.6, Y의 분산은 2, 공분산은 0
X 와 Y의 분산이 서로 다르고 둘의 공분산이 0이기 때문에 plot이 타원 (Y
의 분산이 더 크기 때문에 가로축으로 길쭉한 모양)
(C) 공분산 행렬이 [[1, 0.8], [0.8, 1]] -> X 와 Y의 분산은 1로 서로 같지만 둘의 공분산은 0.8입니다. 이 때문에 plot이 가로축(Y), 세로축(X)에 정렬되지 않는 모습
-> 한 차원의 값을 알면 다른 차원의 값을 예측하는 데 도움 (양수이면 둘이 서로 양의 관계이구나, 음수이면 서로 음의 관계이구나)
3.3 Maximum Likelihood Estimation
Goal: 최대우도추정(Maximum Likelihood Estimation)을 정규분포의 파라미터 추정에 적용하기 !
단변량 정규분포의 파라메터, θ=(μ,σ)
표본(x)을 해당 정규분포 확률함수에 넣어서 해당 표본이 발생할 확률값 P(x|θ)을 추정 가능
데이터는 있는데 파라미터를 모르면, θ를 고정하고 P(x|θ)가 높게 나오는 θ를 찾아야 함 (목표: 표본을 가장 잘 설명하는 θ 찾기)
예) θ 가 μ 하나뿐이라면
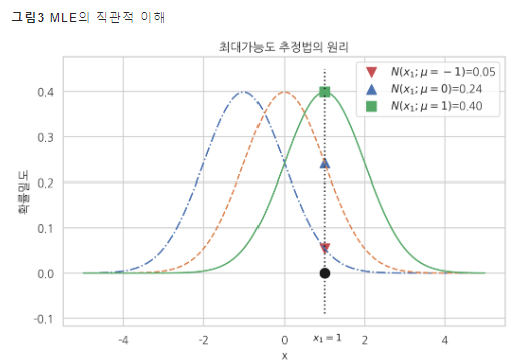
μ=−1 => x=1 이 나타날 확률, 즉 P(x|θ) 는 0.05 (빨간 세모) => 우도(likelihood)
어떤 분포가 가장 표본을 잘 설명? => 우도가 가장 큰 분포 (μ=1)
최대우도추정에 따라 파라미터 추정값은 1이 됨
단변량 정규분포의 파라미터 추정
N개의 표본
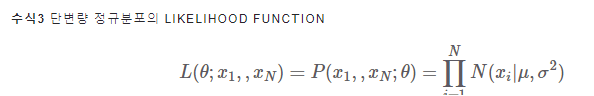
목표: 수식3을 최대화하는 θ 찾기
이때, 확률은 1보다 작아 계속 곱하면 그 값이 지나치게 작아져 언더플로(underflow) 문제
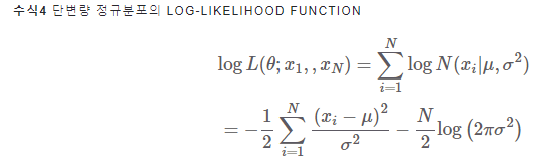
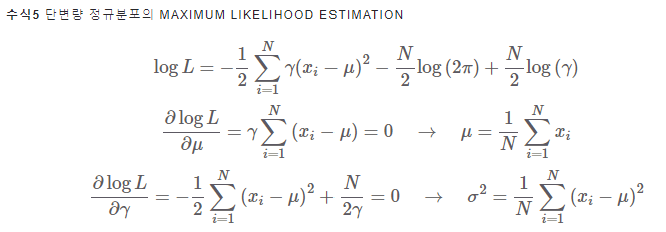
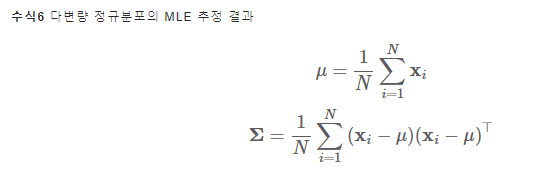
3.4 Gaussian Mixture Model
가우시안 믹스처 모델(Gaussian Mixture Model): M 개의 정규분포의 가중합(weighted sum)으로 데이터를 표현하는 확률 모델
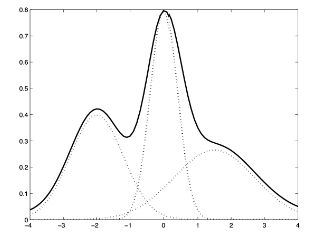
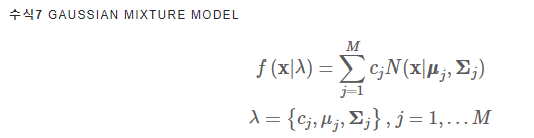
데이터가 정규분포를 따르지 않거나 그 분포가 복잡한 모양(multimodal, not convex)일 경우 사용
파라미터는, 각 정규분포의 평균과 공분산, 가중치임
3.5 Expectation-Maximization
학습을 위해 M개의 정규분포 확률함수(추정 대상 모수 : μ , Σ )와 각각의 가중치(c)를 구해야 함
이를 위해 해당 데이터들이 M개 정규분포 가운데 어디에 속하는지 정보 필요
"두 개를 추정해야 하는 상황"에서 쓰이는 기법 -> Expectation-Maximization 알고리즘
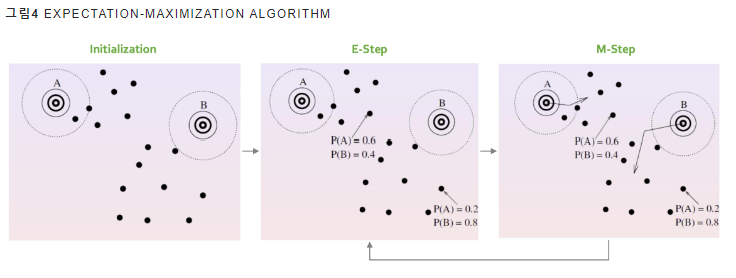
- Initialization 스텝에서 λ 를 랜덤 초기화
- Expectation 스텝에서는 λ 를 고정한 상태에서 모든 데이터에 대해 P(j|x)를 추정 (j: M개 정규분포 가운데 j번째 분포 -> M개 가우시안 확률 함수에 모두 넣어 각각의 확률값을 계산한다 ~~)
- maximization: E-step에서 계산한 확률값을 고정해 놓은 상태에서 λ 를 업데이트
2,3 번 충분히 반복 후 -> 학습 끝 !
2번에서 λ 를 고정한 상태에서 모든 데이터에 대해 가우시안 확률을 추정
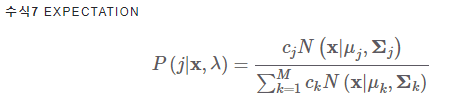
3번에서 수식 7에서 계산한 가우시안 확률을 고정한 상태에서 파라미터 λ 를 업데이트 함
3.6 Modeling Speech Recognition
음성인식에서 MFCC 피처가 정규분포를 따르지 않아 -> M개 다변량 정규분포확률 함수를 합친 가우시안 믹스처 모델로 모델링함
다변량 정규분포의 공분산 행렬을 Full Covariance Marix로 모델링할 경우 성능이 좋음 -> 피처의 각 차원을 개별 확률 변수로 바꾸면, 각 확률 변수 간 상관관계가 존재할 수 있고, 포착이 가능해서
그러나 가우시안 믹스처 모델이 수렴이 늦어질 수 있고 데이터도 많이 필요하다는 단점
그래서 계산량 감소와 수렴 가속화를 위해 공분산이 diagnoal임을 가정해서 -> 대각 성분만 추정해 계산 효율성을 도모함
가정에 맞지 않는 데이터가 들어오면 모델 성능은 이때 낮아짐 -> 그렇기에 가우시안 믹스처 모델의 입력 데이터는 decorrelation을 확실히 해야 함