sklearn이나 기타 다른 라이브러리들을 사용하지 않고 경사하강법을 이용한 선형회귀모델 코드를 작성해보자.
다른 라이브러리를 이용해서 머신러닝 모델을 만들면, 편리하지만 그 속의 코드는 알 수가 없다. 어떤 식으로 흘러가고 어떤 과정을 거치는지 하나하나 살펴보고 이해했을때 라이브러리를 더 잘 활용 할 수 있을 것이다.
데이터
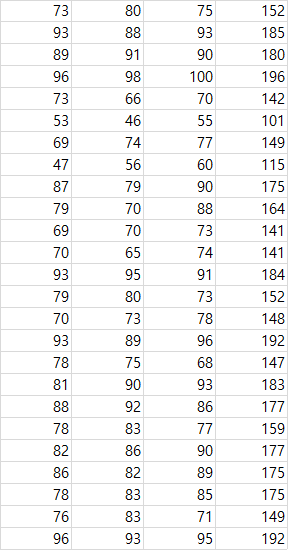
csv.데이터(25x4): 1~3열은 x1,x2,x3로 예를들어, 국어 영어 수학 성적이라 하면 4열(t)은 국어 영어 수학 점수를 바탕으로 나오는 총 수능점수라 생각하면 이해가 편하다.
이 데이터를 바탕으로 국어 영어 수학 점수를 넣었을때 예측되는 수능점수(t)를 예상해보는 모델을 만들어 보자.
먼저, 데이터를 불러오고 x_data, t_data를 정의한다.
슬라이싱을 이용해,
x_data는 데이터에서 1~3열 데이터 모두
t_data는 데이터의 4열 데이터 모두 불러왔다.
import numpy as np
#데이터 가져오기
loaded_data = np.loadtxt('./data-01-test-score.csv', delimiter=',', dtype=np.float32)
x_data = loaded_data[ :, 0:-1]
t_data = loaded_data[ :, [-1]]
# 데이터 차원 및 shape 확인
print("x_data.ndim = ", x_data.ndim, ", x_data.shape = ", x_data.shape)
print("t_data.ndim = ", t_data.ndim, ", t_data.shape = ", t_data.shape)
#결과값
x_data.ndim = 2 , x_data.shape = (25, 3)
t_data.ndim = 2 , t_data.shape = (25, 1)가중치 W와 b에 대해서 0~1사이값 중 하나를 나타내는 random.rand함수를 이용해서 임의의 W와 b를 넣어 주고 shape함수를 이용해 행렬을 파악.
W = np.random.rand(3,1) # 3X1 행렬
b = np.random.rand(1)
print("W = ", W, ", W.shape = ", W.shape, ", b = ", b, ", b.shape = ", b.shape)
#결과값
W = [[0.45303291]
[0.60244002]
[0.34127966]] , W.shape = (3, 1) , b = [0.52588524] , b.shape = (1,)
#(랜덤값임을 감안)손실함수 loss_func을 정의한다,
y = np.dot(x,W) + b 의 의미는
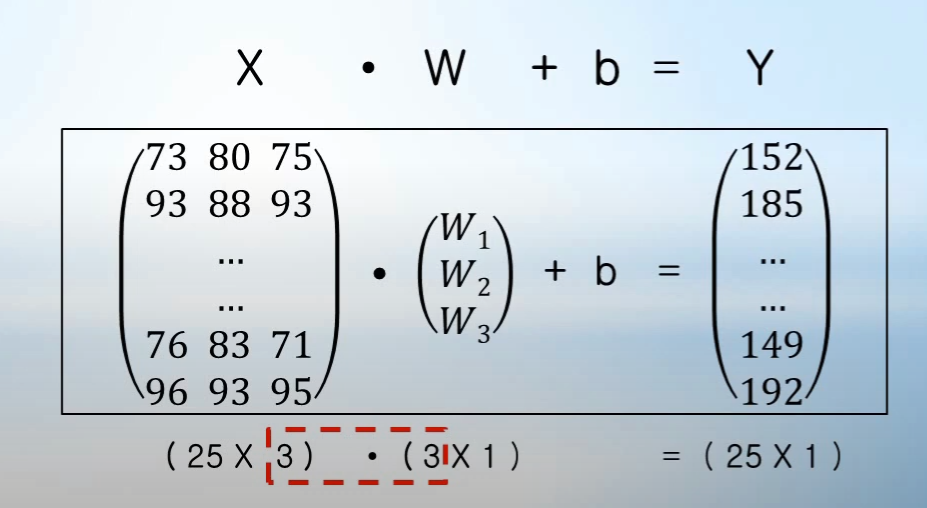
이렇게 x와 W의 행렬곱으로 나타낸다.
def loss_func(x, t):
y = np.dot(x,W) + b
return ( np.sum( (t - y)**2 ) ) / ( len(x) )수치미분 함수 정의
이 함수 numerical_derivative(f, x)는 수치 미분을 사용하여 주어진 함수 f의 입력값 x에서의 기울기(gradient)를 계산하는 함수다. 이 함수는 특히 다차원 배열을 입력으로 받아 각 요소에 대해 개별적으로 편미분을 계산하여 기울기를 구하는 방식이다.
def numerical_derivative(f, x):
# delta_x는 미세한 변화량으로, 수치 미분의 정확성을 높이기 위해 매우 작은 값으로 설정합니다.
delta_x = 1e-4 # 0.0001
# grad는 입력 x와 같은 형태를 가지는 배열로, 각 변수에 대한 기울기(미분 값)를 저장할 것입니다.
grad = np.zeros_like(x)
# np.nditer를 사용하여 다차원 배열 x의 각 요소에 접근할 수 있는 반복자(it)를 생성합니다.
# flags=['multi_index']: 다차원 배열의 각 요소에 대해 인덱스를 사용해 접근할 수 있도록 설정
# op_flags=['readwrite']: 요소를 읽고 쓸 수 있도록 설정
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
# 반복자를 이용해 배열의 모든 요소를 순회하면서 각 요소에 대한 미분을 계산합니다.
while not it.finished:
# 현재 요소의 인덱스를 가져옵니다 (예: 다차원 배열일 경우 (i, j) 형태).
idx = it.multi_index
# 현재 인덱스 위치의 원래 값을 저장해 둡니다. 나중에 원래 값으로 복원해야 합니다.
tmp_val = x[idx]
# x의 현재 요소를 delta_x만큼 증가시켜 f(x + delta_x)를 계산합니다.
x[idx] = float(tmp_val) + delta_x
fx1 = f(x) # f(x + delta_x)의 값을 fx1에 저장
# x의 현재 요소를 delta_x만큼 감소시켜 f(x - delta_x)를 계산합니다.
x[idx] = tmp_val - delta_x
fx2 = f(x) # f(x - delta_x)의 값을 fx2에 저장
# 중심 차분 방식(central difference)을 이용해 현재 요소의 기울기를 계산하여 grad 배열의 해당 위치에 저장합니다.
grad[idx] = (fx1 - fx2) / (2 * delta_x)
# 계산이 끝났으므로 x의 현재 요소를 원래 값으로 복원합니다.
x[idx] = tmp_val
# 다음 요소로 이동합니다.
it.iternext()
# 각 요소에 대한 미분 값을 포함한 grad 배열을 반환합니다.
return grad
# 손실함수 값 계산 함수
# 입력변수 x, t : numpy type
def error_val(x, t):
y = np.dot(x,W) + b
return ( np.sum( (t - y)**2 ) ) / ( len(x) )
# 학습을 마친 후, 임의의 데이터에 대해 미래 값 예측 함수
# 입력변수 x : numpy type
def predict(x):
y = np.dot(x,W) + b
return y경사하강법(Gradient Descent)
손실 함수 값을 최소화하면서 가중치 W와 바이어스 b를 학습하는 과정을 나타냅니다. 주어진 함수 f의 기울기를 구해 W와 b를 점진적으로 업데이트하며 손실 함수 값을 최소화합니다.
# 학습률이 작을수록 W와 b가 조금씩 변화하면서 학습이 안정적으로 진행
learning_rate = 1e-5 # 1e-2, 1e-3 은 손실함수 값 발산
f = lambda x : loss_func(x_data,t_data)
#초기 W와 b의 값에서의 손실 함수 값(오차 값)을 출력하여 학습 전의 상태를 확인합니다.
print("Initial error value = ", error_val(x_data, t_data), "Initial W = ", W, "\n", ", b = ", b )
for step in range(10001):
W -= learning_rate * numerical_derivative(f, W)
b -= learning_rate * numerical_derivative(f, b)
# 400번의 스텝마다 현재의 스텝 번호, 손실 함수 값, 가중치 W, 편향 b를 출력
if (step % 400 == 0):
print("step = ", step, "error value = ", error_val(x_data, t_data), "W = ", W, ", b = ",b )
결과값
Initial error value = 3633.713079764695 Initial W = [[0.66113631]
[0.15238668]
[0.45735755]]
, b = [0.87742641]
step = 0 error value = 1351.6136421317879 W = [[0.75715156]
[0.2490719 ]
[0.5564304 ]] , b = [0.87815007]
step = 400 error value = 11.517862335045466 W = [[0.85333743]
[0.40061573]
[0.75991527]] , b = [0.87893892]
step = 800 error value = 10.470394453972418 W = [[0.80549295]
[0.4037606 ]
[0.80334491]] , b = [0.87854739]
step = 1200 error value = 9.641176246081633 W = [[0.76228704]
[0.40806667]
[0.84113239]] , b = [0.87810669]
step = 1600 error value = 8.982135927704448 W = [[0.72326419]
[0.41318559]
[0.8740607 ]] , b = [0.87762313]
step = 2000 error value = 8.456464166970093 W = [[0.68801456]
[0.4188409 ]
[0.90279825]] , b = [0.87710217]
step = 2400 error value = 8.035809487485311 W = [[0.65616923]
[0.4248149 ]
[0.92791627]] , b = [0.8765485]
step = 2800 error value = 7.698210499550071 W = [[0.62739602]
[0.43093774]
[0.94990352]] , b = [0.8759662]
step = 3200 error value = 7.426563011017449 W = [[0.60139569]
[0.43707847]
[0.96917874]] , b = [0.87535882]
step = 3600 error value = 7.207477146545878 W = [[0.57789863]
[0.44313761]
[0.98610112]] , b = [0.8747294]
step = 4000 error value = 7.030420207259823 W = [[0.55666181]
[0.44904109]
[1.00097922]] , b = [0.87408062]
step = 4400 error value = 6.887069952822725 W = [[0.53746612]
[0.45473521]
[1.01407841]] , b = [0.87341481]
step = 4800 error value = 6.770823682066446 W = [[0.52011398]
[0.46018255]
[1.02562728]] , b = [0.87273398]
step = 5200 error value = 6.676423323540175 W = [[0.50442715]
[0.46535856]
[1.035823 ]] , b = [0.8720399]
step = 5600 error value = 6.599667416573174 W = [[0.49024481]
[0.47024889]
[1.04483587]] , b = [0.87133412]
step = 6000 error value = 6.537188563918138 W = [[0.47742184]
[0.47484707]
[1.05281325]] , b = [0.87061799]
step = 6400 error value = 6.486280516620874 W = [[0.46582724]
[0.47915273]
[1.05988277]] , b = [0.86989271]
step = 6800 error value = 6.444763111947705 W = [[0.45534277]
[0.48317014]
[1.06615519]] , b = [0.86915931]
step = 7200 error value = 6.410876253448538 W = [[0.44586165]
[0.48690698]
[1.07172676]] , b = [0.86841871]
step = 7600 error value = 6.383196303053919 W = [[0.43728744]
[0.49037344]
[1.07668123]] , b = [0.86767173]
step = 8000 error value = 6.360569865861413 W = [[0.42953306]
[0.4935814 ]
[1.08109162]] , b = [0.86691907]
step = 8400 error value = 6.342061144622187 W = [[0.42251982]
[0.49654388]
[1.08502167]] , b = [0.86616137]
step = 8800 error value = 6.326909934649446 W = [[0.41617666]
[0.49927455]
[1.08852708]] , b = [0.86539918]
step = 9200 error value = 6.314498001480959 W = [[0.41043934]
[0.50178735]
[1.09165664]] , b = [0.864633]
step = 9600 error value = 6.304322091390142 W = [[0.40524984]
[0.50409622]
[1.09445314]] , b = [0.86386327]
step = 10000 error value = 6.295972211058345 W = [[0.4005557 ]
[0.50621487]
[1.09695412]] , b = [0.86309037]test_data = np.array([100, 98, 81])
predict(test_data)
#결과값
array([179.38100177])이렇게 numpy만을 이용하여 기본적인 다항회귀모델을 만들어 실행 해 보았다.
기존에 라이브러리를 사용해서 만들었을때 쉽고 간편하게 만들었었는데, 이렇게 하나하나 과정을 보고 배우며 모델을 만드니 복잡하고 코드도 길어졌지만, 동작원리를 더 직관적이게 알 수 있었다.
수치미분을 시행하고, 경사하강법을 실시하는 코드를 직접 구현 해 보니 이해가 잘됐다. 끝
