머신러닝에서 미분의 역할과 인사이트(예시)

2star_·2024년 11월 5일
DerivativeML
0

ML/DL

목록 보기
17/18
post-thumbnail

머신러닝에서 미분의 역할과 인사이트

미분은 머신러닝에서 모델을 학습시키는 핵심 도구 중 하나입니다. 특히 딥러닝과 같은 모델에서 미분을 통해 파라미터(가중치)를 조정함으로써 모델의 예측 성능을 향상시킵니다.

1. 미분의 개념과 역할

1.1 미분의 개념

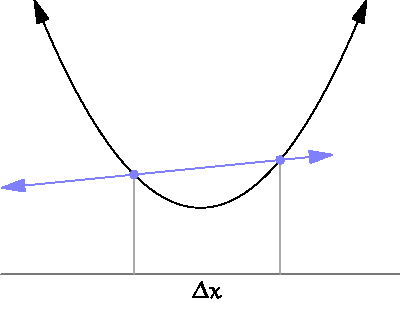
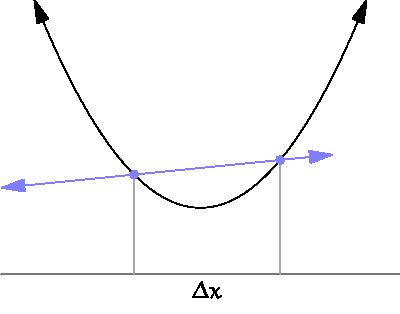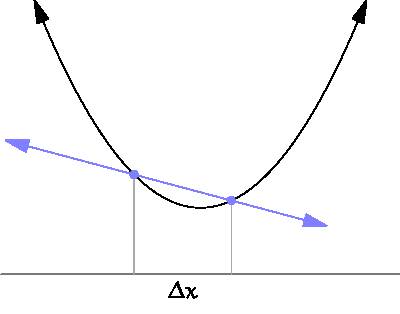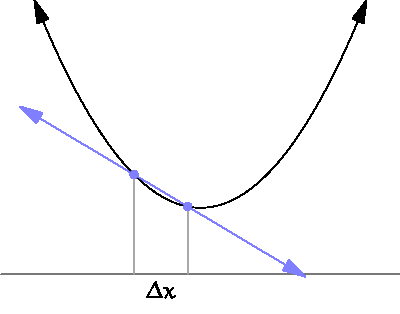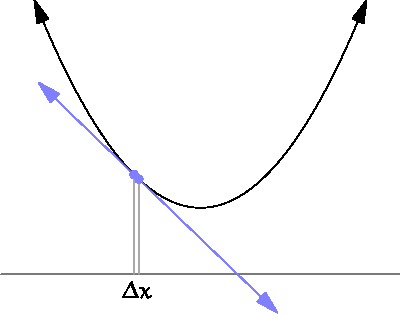
미분은 함수의 변화를 측정하는 도구입니다. 수학적으로는, 어떤 함수 f(x)f(x)가 있을 때, 특정 점 xx에서의 미분값은 그 점에서의 기울기를 의미합니다. 이를 통해 함수가 특정 점에서 증가하는지, 감소하는지, 혹은 어느 방향으로 변화하는지를 알 수 있습니다.

출처
(By Brnbrnz - 자작, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=43249235)

1.2 머신러닝에서 미분의 역할

머신러닝 모델, 특히 딥러닝 모델은 주어진 데이터를 학습하여 목표 함수(예: 손실 함수)를 최소화하도록 합니다. 여기서 손실 함수는 모델의 예측과 실제 값 간의 차이를 측정하는 함수입니다. 미분은 이 손실 함수가 어느 방향으로 변화하는지를 나타내주며, 손실을 줄이기 위해 가중치를 어떻게 조정해야 하는지를 알려줍니다. 즉, 미분값을 통해 모델이 더 좋은 예측을 하도록 가중치를 업데이트하는 방식입니다.

2. 기울기와 최적화 (Gradient and Optimization)

딥러닝에서 가장 널리 쓰이는 최적화 알고리즘은 경사하강법(Gradient Descent)입니다. 경사하강법은 다음과 같은 단계를 거칩니다.

  1. 손실 함수의 기울기를 계산하여, 현재 모델의 파라미터가 손실을 줄이기 위해 어느 방향으로 이동해야 하는지를 알아냅니다.
  2. 계산된 기울기를 반영해 파라미터를 조정합니다. 이 때 조정할 크기를 학습률이라고 부릅니다.

기울기 계산의 예제

예를 들어, 모델이 y=w⋅x+by = w \cdot x + b의 형태를 가진다고 가정해보겠습니다. 여기서 ww와 bb는 학습해야 하는 파라미터입니다. 손실 함수 L(w,b)L(w, b)가 모델 예측과 실제 값 사이의 차이로 정의될 때, 이를 최소화하는 것이 학습의 목표입니다.

이때, 미분을 사용해 각 파라미터에 대한 손실 함수의 기울기 ∂L∂w\frac{\partial L}{\partial w}와 ∂L∂b\frac{\partial L}{\partial b}를 계산합니다. 이 기울기는 파라미터가 어떻게 변해야 손실이 줄어드는지를 알려주며, 경사하강법에 따라 다음과 같이 업데이트합니다:

w=w−α⋅∂L∂ww = w - \alpha \cdot \frac{\partial L}{\partial w}
b=b−α⋅∂L∂bb = b - \alpha \cdot \frac{\partial L}{\partial b}

여기서 α\alpha는 학습률입니다.

3. 미분으로 얻을 수 있는 인사이트

미분을 통해 머신러닝 모델이 최적화 과정에서 어떤 동작을 하는지 이해할 수 있습니다.

  1. 손실 함수의 변화를 분석할 수 있습니다. 미분값이 0에 가까운 경우, 손실 함수가 극소값(최소값 또는 최저점)에 도달했다는 것을 의미합니다.
  2. 학습 과정의 방향성과 속도를 파악할 수 있습니다. 미분값이 크다면, 모델의 예측이 목표값과 많이 차이나며 빠르게 변화를 줄 필요가 있다는 의미입니다.
  3. 오버슈팅(overshooting) 가능성을 피할 수 있습니다. 미분을 통해 기울기를 과도하게 따라가지 않도록 조절할 수 있으며, 이를 통해 안정적인 학습이 가능해집니다.

4. 실제 예제: 단순 선형 회귀에서 미분의 사용

단순한 예로, 선형 회귀 모델을 사용하여 집 값 예측 문제를 해결한다고 가정해봅시다. 모델은 다음과 같습니다:

y=w⋅x+by = w \cdot x + b

여기서 yy는 예측 값, xx는 집의 크기, ww는 기울기, bb는 절편입니다. 손실 함수로는 평균 제곱 오차(MSE)를 사용하며, 이는 다음과 같이 정의됩니다:

L(w,b)=1N∑i=1N(yi−(w⋅xi+b))2L(w, b) = \frac{1}{N} \sum_{i=1}^{N} (y_i - (w \cdot x_i + b))^2

여기서 yiy_i는 실제 값, NN은 데이터의 개수입니다.

  1. 미분값 계산: 손실 함수를 ww와 bb에 대해 각각 미분하여, ∂L∂w\frac{\partial L}{\partial w}와 ∂L∂b\frac{\partial L}{\partial b}를 얻습니다.
  2. 파라미터 업데이트: 경사하강법을 사용하여, 미분값에 따라 ww와 bb를 반복적으로 업데이트합니다.

이 과정을 통해 모델의 예측이 점점 실제 값에 가까워지게 됩니다.

5. 편미분의 개념과 머신러닝에서의 역할

5.1 편미분의 개념

편미분은 다변수 함수에서 특정 변수에 대한 변화율을 계산하는 방법입니다. 즉, 여러 개의 입력 변수 중 하나의 변수에만 초점을 맞추어, 나머지 변수들은 고정시킨 채로 해당 변수에 대한 변화율을 측정합니다. 예를 들어 함수 f(x,y)f(x, y)에서 xx에 대한 편미분을 구한다면, yy는 고정된 값으로 취급하고 xx의 변화에 따라 ff가 어떻게 변하는지를 측정합니다.

수식으로 표현하면, f(x,y)f(x, y)에서 xx에 대한 편미분은 다음과 같습니다:

∂f∂x\frac{\partial f}{\partial x}

이때 ∂\partial 기호는 편미분을 나타내며, ff가 xx에 대해서만 변하는 경우의 변화율을 뜻합니다.

5.2 머신러닝에서 편미분의 역할

머신러닝 모델, 특히 딥러닝 모델은 다수의 파라미터(가중치와 편향)를 가지고 있습니다. 각 파라미터는 모델의 예측 성능에 영향을 미치므로, 이를 학습시키기 위해서는 각각의 파라미터에 대한 손실 함수의 변화를 개별적으로 계산해야 합니다. 여기서 편미분이 사용됩니다.

편미분을 통해 각 파라미터가 손실 함수에 미치는 영향을 따로따로 계산할 수 있으며, 이를 활용해 경사하강법 등 최적화 알고리즘에서 각 파라미터를 개별적으로 업데이트할 수 있습니다. 이 과정은 체인 룰(chain rule)에 의해 서로 연결되어 파라미터 전체가 동시에 최적화되도록 합니다.

6. 예제: 편미분을 통한 다중 변수 모델 최적화

예제 1: 다중 선형 회귀

다중 선형 회귀 모델을 예로 들어보겠습니다. 이 모델은 다음과 같은 형태를 가집니다:

y=w1⋅x1+w2⋅x2+⋯+wn⋅xn+by = w_1 \cdot x_1 + w_2 \cdot x_2 + \cdots + w_n \cdot x_n + b

여기서 w1,w2,…,wnw_1, w_2, \ldots, w_n은 모델의 가중치, bb는 절편, x1,x2,…,xnx_1, x_2, \ldots, x_n은 입력 변수입니다. 손실 함수로는 평균 제곱 오차(MSE)를 사용하며, 다음과 같이 정의됩니다:

L(w1,w2,…,wn,b)=1N∑i=1N(yi−(w1⋅xi1+w2⋅xi2+⋯+wn⋅xin+b))2L(w_1, w_2, \ldots, w_n, b) = \frac{1}{N} \sum_{i=1}^{N} (y_i - (w_1 \cdot x_{i1} + w_2 \cdot x_{i2} + \cdots + w_n \cdot x_{in} + b))^2

이제 각각의 가중치 wjw_j에 대해 편미분을 수행하여 ∂L∂wj\frac{\partial L}{\partial w_j} 값을 계산합니다. 이 과정은 각 가중치가 손실 함수에 얼마나 영향을 미치는지를 개별적으로 분석해 주므로, 최적화 알고리즘이 이를 바탕으로 각 가중치를 개별적으로 조정할 수 있습니다. 이 편미분 값은 다음과 같은 방식으로 경사하강법에 사용됩니다:

wj=wj−α⋅∂L∂wjw_j = w_j - \alpha \cdot \frac{\partial L}{\partial w_j}

여기서 α\alpha는 학습률입니다.

예제 2: 딥러닝 모델의 편미분 (백프로파게이션)

딥러닝에서는 많은 층(layer)을 가진 네트워크에서 파라미터 업데이트를 효율적으로 수행해야 합니다. 이때 각 층의 가중치와 편향을 조정하기 위해 백프로파게이션(backpropagation)이라는 알고리즘을 사용합니다. 백프로파게이션은 각 층의 가중치에 대한 손실 함수의 편미분을 구해, 이를 통해 전체 네트워크가 학습할 수 있도록 합니다.

  1. 순전파(forward pass): 입력 데이터를 네트워크에 통과시키면서 예측 값을 얻습니다.
  2. 손실 계산: 예측 값과 실제 값 간의 손실을 계산합니다.
  3. 역전파(backward pass): 손실을 최소화하기 위해, 각 파라미터에 대한 편미분을 계산하여 경사를 구합니다.
  4. 파라미터 업데이트: 경사하강법을 통해 각 파라미터를 업데이트합니다.

이 과정을 반복하면서 딥러닝 모델이 점차 학습되어, 목표한 성능에 도달하게 됩니다.

7. 편미분으로 얻을 수 있는 추가 인사이트

  1. 파라미터의 개별 중요성: 편미분을 통해 특정 변수나 가중치가 손실 함수에 얼마나 큰 영향을 미치는지 파악할 수 있습니다.
  2. 복잡한 모델 학습의 효율성: 편미분을 통해 다변수 함수의 변화를 계산하므로, 수천만 개의 파라미터를 가진 복잡한 딥러닝 모델에서도 학습을 효율적으로 수행할 수 있습니다.
  3. 파라미터 간 상관 관계 분석: 여러 변수의 편미분을 통해 파라미터 간의 상호 작용을 이해하고, 모델의 성능을 개선하기 위해 어떤 변수를 조정해야 하는지를 결정할 수 있습니다.

8. 편미분 예제: 체중 변화 모델

편미분의 실생활 예로, 체중이 "야식"과 "운동"에 영향을 받는다고 가정해봅시다. 체중을 함수 f(야식,운동)f(\text{야식}, \text{운동})로 정의할 수 있으며, 이 함수는 두 변수, 즉 "야식"과 "운동"에 따라 달라집니다.

가정

  • 야식: 현재 섭취하는 야식의 양을 나타내며, 야식의 양을 줄이거나 늘리는 것이 체중에 영향을 미칠 수 있습니다.
  • 운동: 현재 하는 운동량을 나타내며, 운동량을 늘리거나 줄이는 것이 체중에 영향을 미칠 수 있습니다.

이때 편미분을 이용하면, 두 변수를 독립적으로 분석하여 각각의 변화가 체중에 어떤 영향을 미치는지 구할 수 있습니다.

편미분의 의미

  1. ∂체중∂야식\frac{\partial \text{체중}}{\partial \text{야식}}: 현재 섭취하는 야식의 양에서 작은 변화를 줄 경우, 체중이 얼마나 변하는지를 나타냅니다. 이는 야식의 변화가 체중에 미치는 직접적인 영향을 측정하는 것입니다.
  2. ∂체중∂운동\frac{\partial \text{체중}}{\partial \text{운동}}: 현재 하고 있는 운동량에서 작은 변화를 줄 경우, 체중이 얼마나 변하는지를 나타냅니다. 이 값은 운동량의 변화가 체중에 미치는 직접적인 영향을 나타냅니다.

예제 설명

만약 체중이 야식과 운동에 의해 복합적으로 영향을 받는다고 한다면, 각각의 변수에 대해 편미분을 수행하여 개별적인 영향을 분석할 수 있습니다. 예를 들어, 야식을 줄이면 체중이 감소할 가능성이 높고, 운동량을 늘리면 역시 체중이 감소할 가능성이 높습니다. 편미분은 이처럼 각 요인의 변화가 체중에 미치는 효과를 따로따로 측정하여, 체중 관리에 있어 어떤 요인이 더 중요한 역할을 하는지 판단하는 데 도움을 줄 수 있습니다.

profile
2star_
안녕하세요.
이전 포스트

ML 지도학습의 회귀 모델: 선형회귀, 다항회귀, 리지회귀, 라쏘회귀

다음 포스트

numpy만 이용해 머신러닝 Linear Regression 만들기

0개의 댓글