Deeper Look at GD

📒 Gradient Descent

---

Bias가 없는 간단한 식으로 경사하강법을 이해해본다.

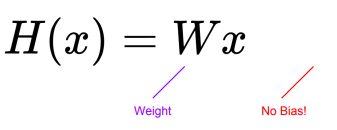
📝 Dummy Data

---

Hours(x)	Points(y)
1	1
2	2
3	3

x_train = torch.FloatTensor([1], [2], [3]])
y_train = torch.FloatTensor([1], [2], [3]])

• H(x) = x가 정확한 모델이다. ( W = 1 이 가장 좋은 숫자이다.)

📝 Cost function

---

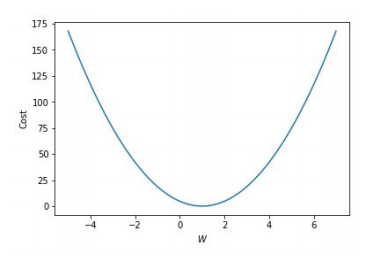
• W = 1 일 때 cost = 0이며, 1에서 멀어질수록 높아진다.
  
• Mean Squared Error(MSE)로 오차를 구한다.
  

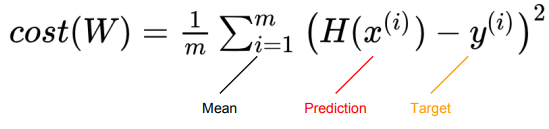
cost = torch.mean((hypothesis - y_train) ** 2)

📝 Gradient descent

---

• 기울기가 양수면 W를 줄이고, 음수이면 W를 늘려야된다.
  

gradient = 2 * torch.mean((W * x_train - y_train) * x_train)
lr = 0.1
W -= lr * gradient

📝 Full code

---

import torch

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1)
# learning rate 설정
lr = 0.1
nb_epochs = 10
for epoch in range(nb_epochs + 1):
    # H(x) 계산
    hypothesis = x_train * W
    # cost gradient 계산
    cost = torch.mean((hypothesis - y_train) ** 2)
    gradient = torch.sum((W * x_train - y_train) * x_train)
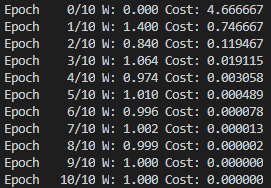
    print('Epoch {:4d}/{} W: {:.3f}, Cost: {:.6f}'.format(
    epoch, nb_epochs, W.item(), cost.item()))
    # cost gradient로 H(x) 개선
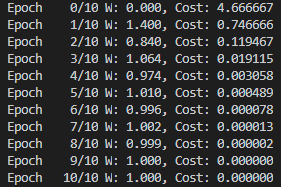
    W -= lr * gradient

• 점점 Cost가 줄어드는 모습을 확인할 수 있다.
  

📝 Full code with torch.optim

---

• torch.optim 으로 경사 하강법을 더 쉽게 구현할 수 있다.

import torch

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = torch.optim.SGD([W], lr=0.15)
nb_epochs = 10
for epoch in range(nb_epochs + 1):
    # H(x) 계산
    hypothesis = x_train * W
    # cost 계산
    cost = torch.mean((hypothesis - y_train) ** 2)
    print('Epoch {:4d}/{} W: {:.3f} Cost: {:.6f}'.format(
    epoch, nb_epochs, W.item(), cost.item()))
    # cost로 H(x) 개선
    optimizer.zero_grad() # gradient를 0으로 초기화
    cost.backward()       # gradient 계산
    optimizer.step()      # 경사하강법(W에 적용)

• 역시 1에 수렴하는 W와 줄어드는 cost를 확인할 수 있다.