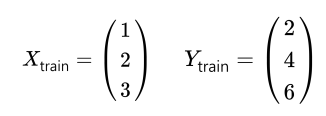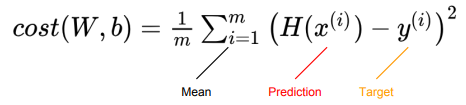Linear regression

📒 선형회귀

---

이거 먼저 읽기

📝 Data definition

---

• 내가 4시간을 공부했을 때 어떤 점수가 나올 것인가?

Hours (x)	Points (y)
1	2
2	4
3	6
4	?

• 데이터는 torch.tensor 형태를 띈다.
• 입력과 출력은 따로 둔다. (x_train, y_train)
  

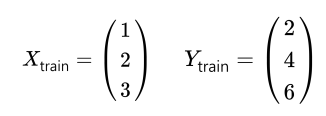
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])

📝 Hypothesis

---

• y = Wx + b 로 식을 정의한다.
• 여기서 W는 weight, b는 Bias를 의미한다.
• W와 B를 0으로 초기화하여 항상 출력 0을 예측한다.

W = torch.zeros(1, requires_grad=True) # 학습할 것이라고 명시
b = torch.zeros(1, requires_grad=True)
hypothesis = x_train * W + b

📝 Compute loss

---

• 학습을 하려면, 모델이 얼마나 정답과 가까운지를 알아야 한다. (cost, loss)
  

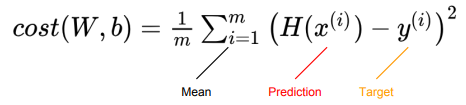
cost = torch.mean((hypothesis - y_train) ** 2)

📝 Gradient descent

---

• torch.optim 라이브러리를 사용한다.
• 참고

optimizer = optim.SGD([W, b], lr=0.01) # [W, b]는 학습할 tensor들, lr은 learning rate

optimizer.zero_grad() # gradient를 초기화
cost.backward() # gradient를 계산
optimizer.step() # W와 b를 개선

📝 Full traning code

---

import torch

x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])

W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)

optimizer = torch.optim.SGD([W, b], lr=0.01)

nb_epochs = 10000
for epoch in range(1, nb_epochs + 1):
    hypothesis = x_train * W + b
    cost = torch.mean((hypothesis - y_train) ** 2)

    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

print(4 * W + b)

• 8이 출력됨을 확인할 수 있다.