DETR: transformers for object detection

DETR(End-to-End Object Detection with Transformers, ECCV 2020)

Introduction

Object detection task can be understood as a combination of two tasks: bounding box regression and label prediction. Bounding box of the object should be located properly, and each box should be predicted with correct label. Anchor based bounding box selection methods, especially utilizing NMS(Non-maximum suppression) algorithms are somehow heuristic.
Was it bad? No! Notably, DETR shows similar or slightly imperior performance compared to Mask R-CNN. However, there is a huge advantage of end-to-end training, it is still important to suggest a methodology which does not rely on heuristic algorithms or prior knowledge.

Architecture

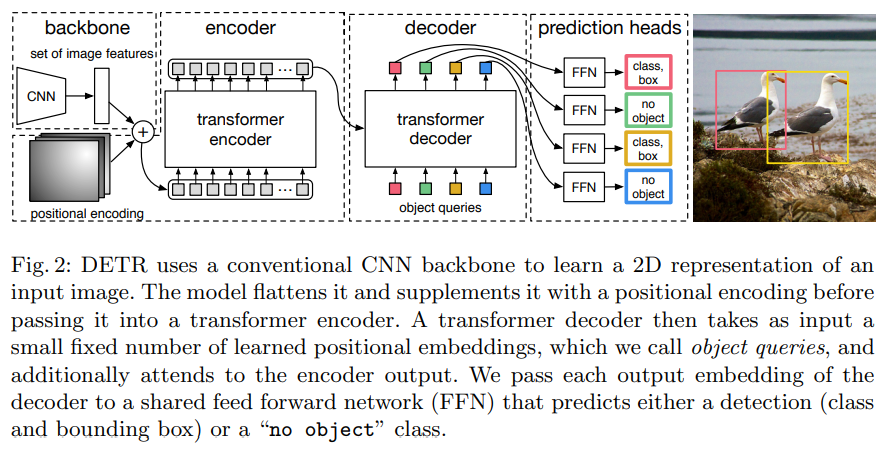
• Features extracted from CNN, flattened, and decorated by positional encoding
• Bbox predictions with transformer encoder-decoder
• Predicted bounding box are regularized by bipartite graph matching with the ground truth
• Bipartite matching loss is suggested, to assign each predicted bounding box into corresponding bounding box in the ground truth.
• Did not utilize any customized block, thus has high scalability: extend to swin transformer, ViT
• Decodes N object in a non-autoregressive manner
  Object detection set prediction loss

Loss function

1. Bipartite matching loss

• Bipartite matching loss is introduced to optimize ideal matching & similarity of matched objects.
• Search space: all permutated pair of bounding boxes(prediction & GT)
• Bipartite matching loss aims to find permutation $\sigma$ s.t.
  $\hat{\sigma} = \arg\min_{\sigma\in\mathcal{G}_N}\sum_{i}^N\mathcal{L}_{match}(y_i,\hat{y_{\sigma(i)}}$

2. $\mathcal{L}_{match}$ : Hungarian algorithm

• $\mathcal{L}_{match}$ is a loss that both reflects class prediction and boundng box similarity
• $\mathcal{L}_{hungarian} = \sum_{i=1}^N[-\log\hat{p_{\sigma_i}}(c_i) + \mathbf{1}_{c_i\not=\phi}\mathcal{L}_{box}(b_i, \hat{b_{\sigma_i}})]$
• Where $\mathcal{L}_{box} = \lambda_{iou}\mathcal{L}_{iou}(b_i,\hat{b_{\sigma(i)}})+\lambda_{L1}||b_i-\hat{b_{\sigma_i}}||_1$