Rethinking residual networks

This article is about 'rethinking residual networks'. ResNet and its relevant works have shown that residual block in deep neural networks enhances optimization of networks. Explanation that "optimization of $h(x) = f(x)-x$ is easier than optimization of $f(x)$", seems plausible.

Is that all? In my personal aspect, impact of residual network seems much larger than previous explanation can cover. Thus, in this article I'll introduce some novel explanations on residual networks and its extensions.

Today, I'll review a paper:
Residual Networks Behave Like Ensembles of Relatively Shallow Networks

Residual Networks Behave Like Ensembles of Relatively Shallow Networks

This paper suggests a novel interpretation of residual networks. They argue that residual networks:

• Behave as a collection of many paths of differing length, which resembeles an ensemble.
• Mainly leverages the shortest paths during training, which enable very deep networks to be robustly trained.

Especially, authors showed that only the short paths are needed during training, as longer paths do not contribute to any gradient.

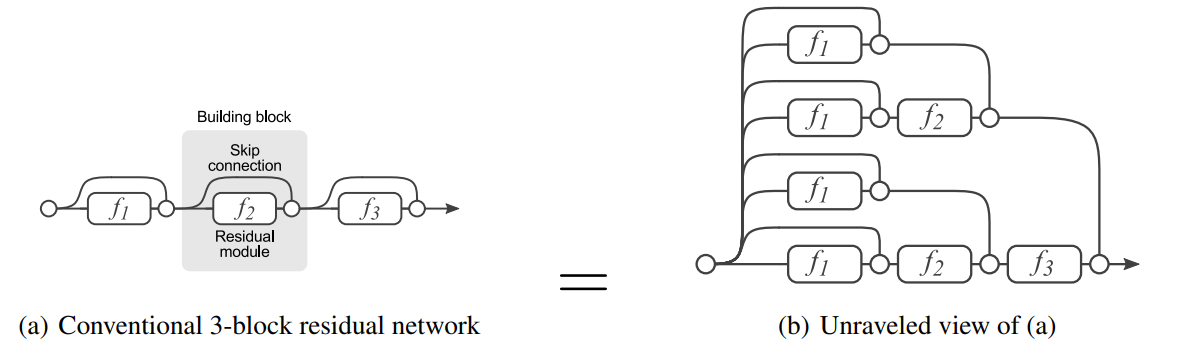
Upper diagram illustrates a novel interpretation of residual network as collection of paths. Key implication is that each paths are 'almost independent', which resembles an ensemble of networks. It is intuitively understandable that skip connection gives an additional pathway to bypass transformation layer. Thus, linchpin of this discussion is about 'how each pathways are related?'.

1) Lesion study: paths in a residual network do not strongly depend on each other

• Deleting individual layers from VGG & ResNet

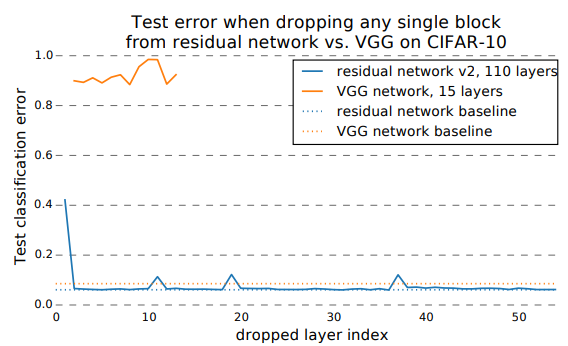
• VGG network's computation flow: $f_1^{FF}(f_2^{FF}(...(f_k^{FF}(x))))$
• ResNet's computation flow: $f_1^{FF}(f_2^{FF}(...(f_k^{FF}(x)+x)+x)...)+x)+x$
• Deletion of single layer corrupts only half the path: half are still preserved. Thus ResNet's classification error remained low.
• This result suggests that paths in a residual network do not strongly depend on each other although they are trained jointly.

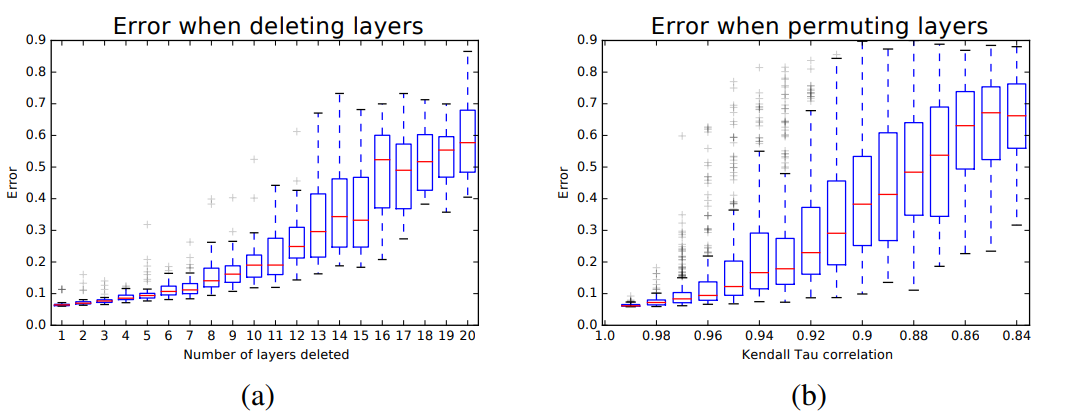
2) Deleting and reordering modules in ResNet

What kind of behavior is expected in ResNet, especially regarding previous 'unravled' formulation? As deleted/reordered modules increase, we can expect that test-time error will also increase gradually. This behavior is expected due to 'ensemble' of subnetworks ResNet: unlike VGGNet which has single pathway of data flow. Experiment results suggested in this paper support theoretical expectations.

3) Importance of short paths in ResNet

How much gradient do the paths of different lengths contribute in a residual network? We already know the fact that ResNet with about 110 layers is also optimized easily, just like shallower VGGNets. This observation implies that "Effective path length" in ResNet is much shorter than the number of layers we stacked. Theoretically, length of each paths composing a 110-layer ResNet follows a binomial distribution $\mathcal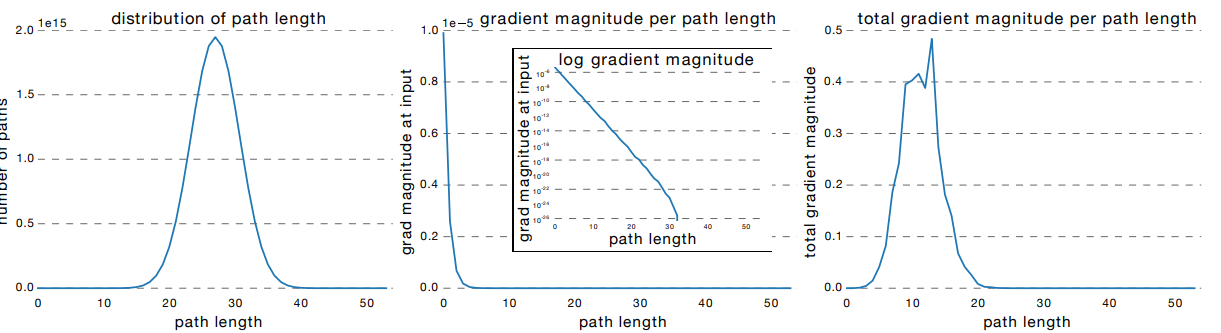{B}(110, 0.5)$ : Figure (a).

However, by calculating grdients, the gradient magnitude peak occurs at smaller path length. This implies that gradient backpropagation mainly rely on shorter paths, while there are longer path alternatives: Figure (c). It is also supported by the observation that gradient magnitude exponentially decreases as the path length gets longer: Figure(b).

4) Discussion

To conclude these observations and explanations, ResNet can be interpreted as a combination of main identity network $I(x)$ and auxiliary network(which means transformation layers) that manipulate the details of identity flow.

ResNet paradigm suggests a flip of thought: "Let's first map the input data with identity transformation. This is the main flow, and layer(convolutional) is just an auxiliary transformations that manipulate the detail in input data!"

This provides a explanation about the question "Why U-Net is so powerful in semantic segmentation?". U-Net is oddly powerful, compared to the performance of various residual-connection based models in different tasks. Especially in semantic segmentation, each pixel of input image and output segmentation map can form a 1-1 correspondance relationship. In this situation, identity flow provides a powerful estimation of segmentation map. However, for image classification, pixel-wise detail of input image itself is not a powerful estimation of classification result: global and local context matters more.