Clustering

Partitioning methods

K-means

• outlier에 민감
• 초기 중심값에 민감(랜덤하게 부여하기 때문에)

K-means++

• 초기 중심점 선정의 어려움을 해결하기 위한 방법
• 실제 레코드(데이터포인트)를 초기 중심점 선정에 활용

  1. 무작위로 1개 레코드 선택(첫번째 중심점)
  2. 해당 중심점과 나머지 레코드 간의 거리 계산
  3. 가장 먼 레코드를 다음 중심점으로 지정
  4. 중심점이 k개가 될때까지 2-3번 반복

MiniBatchkMeans

• 빨라서 더 많이 사용

from sklearn.cluster import MiniBatchKMeans
kmeans = MiniBatchKMeans(n_clusters=10)
kmeans.fit(x)

Mean Shift

• 중심을 기준으로 일정 반경 내를 같은 클러스터로 부여
• 반경 내의 레코드들의 평균값으로 중심 없데이트
• 이상치 제거에 좋다. 반경에 들어오지 못하는 데이터를 이상치로 보고 걸러내기

Hierarchical Methods

Agglomerative Clustering(AGNES)

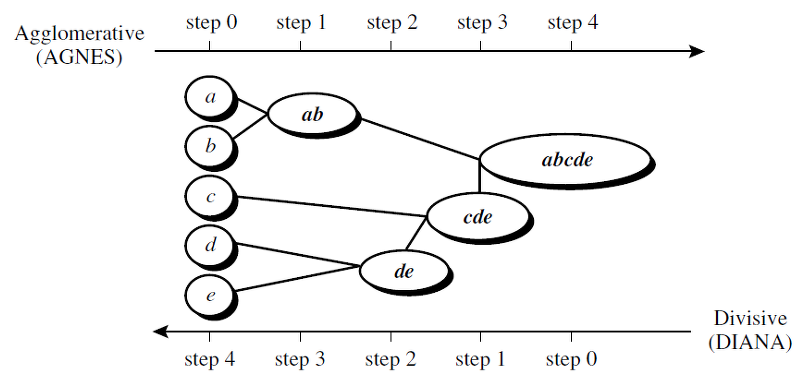
BIRCH

• 분할 기법을 결합한 계층적 군집화

Density-based Methods

DBSCAN

• 레코드들이 몰려있는(밀도가 높은) 데이터 지역을 탐색
• 시간 오래걸림
• sparse 데이터에는 적합하지 않음
• Silhoutte Score 사용 부적절
• 군집 k값 안정해줘도 됨

# 군집 개수 확인
dbscan.core_sample_indices_.shape

OPTICS

• DBSCAN과 거의 유사하나 좀더 빠름?

# 군집 개수 확인
dbscan.cluster_hierarchy.shape

Clustering 성능 평가

• 사전 정의되 군집이 있는 경우 : 주로 v-measure
• 사전 정의된 군집이 없는 경우 : Silhouette Coefficient
  • 군집 내의 거리는 짧을 수록, 군집 간의 거리는 길수록 좋은 군집화
  • 실루엣 계수 높을 수록 좋음
  • DBSCAN 등의 기법에는 부적합

from sklearn.cluster import MiniBatchKMeans
from sklearn.metrics import silhoutte_score

X= np.array(x_).reshape(-1,1)
result =[]

for k in range(3, 20):
	kmeans = MiniBatchKMeans(n_clusters=k)
    kmeans.fit(X)
    pred = kmeans.predict(X)
    result.append([kmeans.inertia_, silhouette_score(X, pred)])
# Inertia value는 군집화가 된 후에, 각 중심점에서 군집의 데이터간의 거리를 합산한 것이므로, 군집의 응집도를 나타내는 값.

results = pd.DataFrame(results).reset_index()
results.columns = ['k', 'Inertia', 'Silhouette']
results['k'] +=2 
results

# results에서 가장 적합한 k값을 찾은 후 
kmeans = MiniBatchKMeans(n_clusters=7)
kmeans.fit(X)

# 클러스터 중심과 할당된 클러스터 확인
cluster_centers = kmeans.cluster_centers_
labels = kmeans.labels_

# 클러스터별 데이터 수 확인 
unique_labels =np.unique(labels)
for label in unique_labels:
	cluster_data = X[labels == label]
    print(f"Cluster {label}: {cluster_data.fatten()}"

# 시각화 
plt.scatter(X, np.zeros_like(X), c= labels, cmap='viridis')
plt.scatter(cluster_centers, np.zeros_like(cluster_centers), marker='x', s=200, color='red')
plt.title('KMeans Clustering for 1D Data')
plt.xlabel('Feature 1')
plt.show()