정렬

정렬이란?

만약에 우리가 구슬들을 크기별로 나열해야 한다면 어떻게 하면 될까? 제일 큰 것부터 찾을 수도 있고 일단 분류해서 정리하는 경우도 있을 것이다. 이러한 행동을 우리는 정렬이라고 부른다.
정렬은 앞서 살펴본 것처럼 요소들을 일정한 순서대로 열거하는 알고리즘이다. 정렬 알고리즘은 우리가 실제로 순서를 정리할 때 사고하는 절차와 거의 유사하다.

정렬의 특징

• 정렬 기준은 사용자가 정할 수 있다. 무슨 값을 기준으로 할 지 오름차순일지 내림차순일지 정할 수 있다.
• 크게 비교식 정렬과 분산식 정렬로 나눌 수 있다.
• 대부분의 언어가 빌트인으로 제공 해주기 때문에 편리하게 사용할 수 있다.
• 정렬 방식은 다양하다. 삽입, 선택, 버블, 머지, 힙, 퀵 정렬 등의 정렬이 있다. 여기서 말한 정렬 외에도 기수 정렬, 팀 정렬, 스파게티 정렬도 있다.

정렬 알고리즘 중 어떤 것이 제일 빠를까? 퀵 정렬이나 머지 정렬이 제일 빠를 것이라 예상할 수 있다. 하지만 정렬들은 각각 유리한 상황과 불리한 상황이 있기 때문에 무엇이 더 좋고 나쁜지 정해져 있지는 않다.

버블 정렬

다른 요소와 비교를 통해 정렬하는 방식을 말한다. 버블 정렬은 비교식 정렬 중에 하나로 서로 인접한 두 요소를 검사하여 정렬하느 알고리즘이다. 시간 복잡도는 O(n제곱)이 걸린다. 동작 순서는 아래와 같다. 먼저 정렬되지 않은 배열을 보고 이 배열을 오름차순으로 배열해보자.

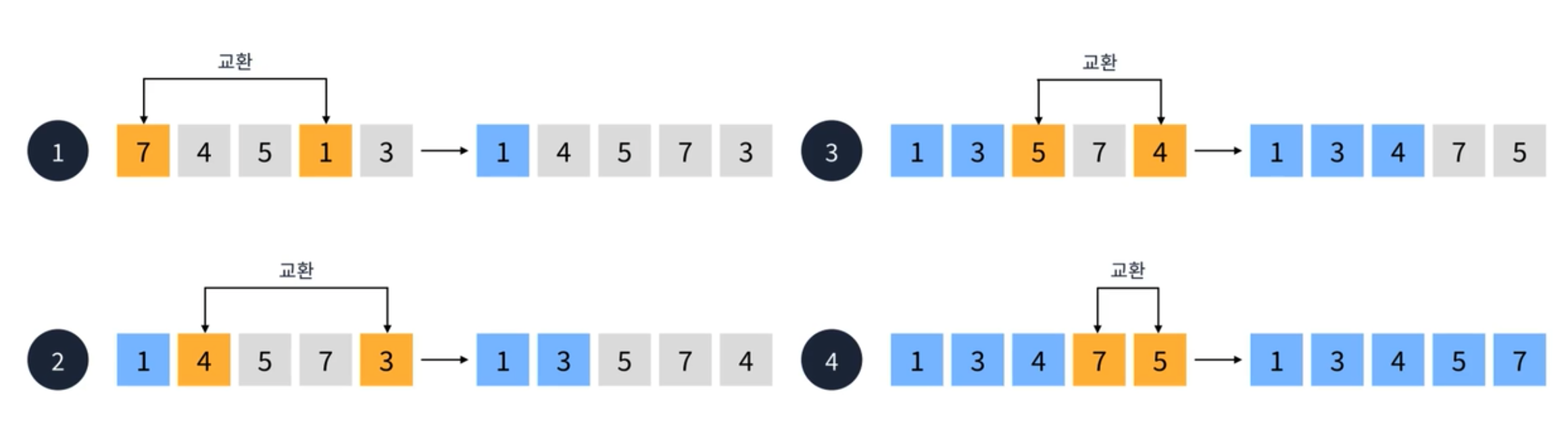
1. 첫번째 요소에서 인접한 요소를 검사한다. 7보다 4가 더 작기 때문에 오름차순에 따라 두 요소를 교환한다.
2. 교환 후 두번째 요소와 세번째 요소를 비교한다. 7보다 5가 더 작기 때문에 교환한다.
3. 교환 후 이어서 세번째 요소와 네번째 요소를 비교한다. 7보다 1이 작기 때문에 교환한다.
4. 마지막으로 네번째 요소와 다섯번째 요소를 비교한다. 7보다 3이 작기 때문에 교환한다.
   
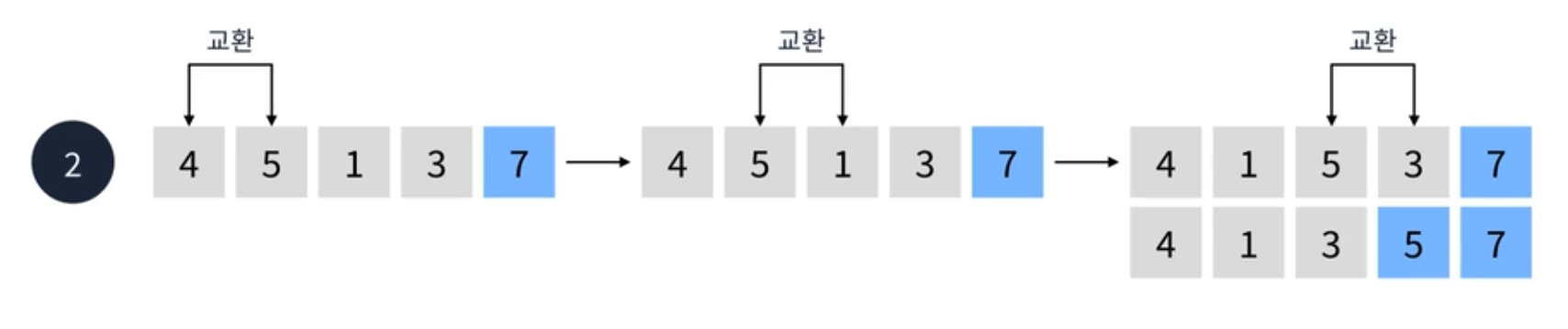
   이렇게 하면 첫번째 순회가 완료된다. 이제 두번째 순회를 진행한다.
5. 첫번째 요소와 두번째 요소를 비교한다. 4가 5보다 작기 때문에 교환하지 않는다.
6. 두번째 요쇼와 세번째 요소를 비교한다. 5가 1보다 크기 때문에 교환한다.
7. 마지막으로 세번째 요소와 네번째 요소를 비교한다.
   
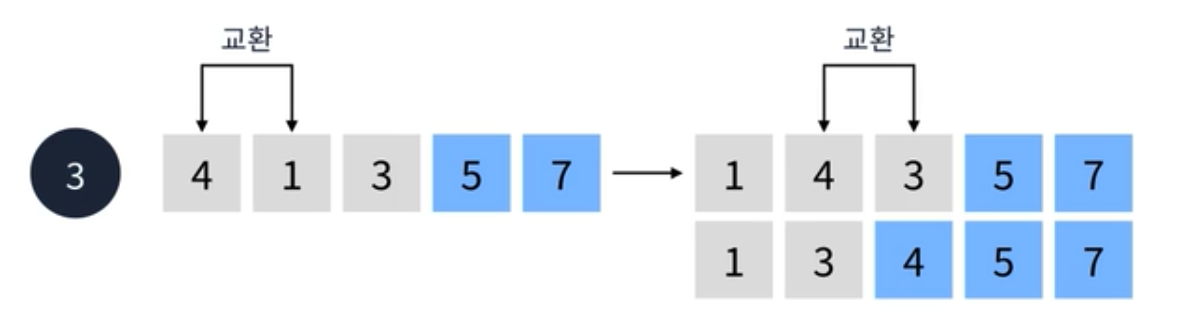
   이어서 세번째 순회를 진행한다.
8. 첫번째와 두번째 요소를 비교한다. 1이 더 작기 때문에 교환한다.
9. 두번째 요소와 세번째 요소를 비교한다. 4가 더 크기 때문에 교환한다.
   
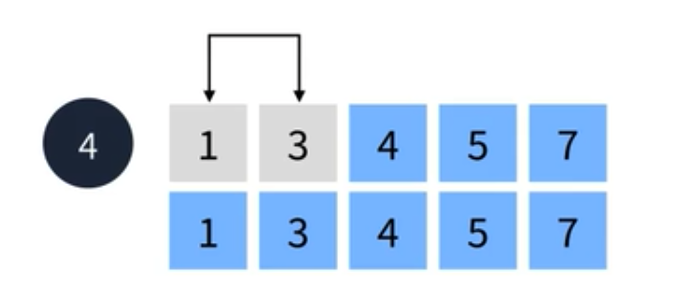
   이렇게 세번째 순회도 마무리 된다. 마지막 순회를 진행한다.
10. 1과 3을 비교한 다음에 교환하지 않고 순회가 마무리 된다.
    
    결국 버블 정렬은 (n - 1)번 순회하면 정렬이 마무리 된다.

선택 정렬

선택 정렬은 사람이 이해하기에 제일 단순한 정렬이라고 볼 수 있다. 선택한 요소와 나머지 요소 중 가장 우선순위가 높은 요소를 정렬 알고리즘이다. 선택 정렬도 마찬가지로 이차 시간 O(n 제곱) 시간복잡도를 가진다. 동작 순서는 아래와 같다.

1. 먼저 선택된 첫번째 요소와 나머지 요소 중 가장 우선 순위가 높은 1과 교환한다.
2. 그 다음 두번째 요소와 나머지 요소 중 가장 우선 순위가 높은 3과 교환한다.이렇게 되면 두개의 요소가 정렬된다.
3. 세번째 요소와 나머지 요소 중 가장 우선 순위가 높은 요소와 교환한다. 세개의 요소가 정렬 되었다.
4. 마지막으로 남은 두 요소를 비교한 후 교환한다.
   
   선택 정렬은 이처럼 간단하다. 참고로 나머지 요소 중 선택된 요소보다 우선 순위가 높은 요소가 없다면 교환을 하지 않고 넘어가면 된다.

삽입 정렬

선택한 요소를 삽입 할 수 있는 위치를 찾아서 삽입하는 방식의 정렬 알고리즘이다. 이차시간 O(n제곱) 시간복잡도를 가진다. 다른 정렬보다 구현하는데 있어서 조금 더 복잡하다.

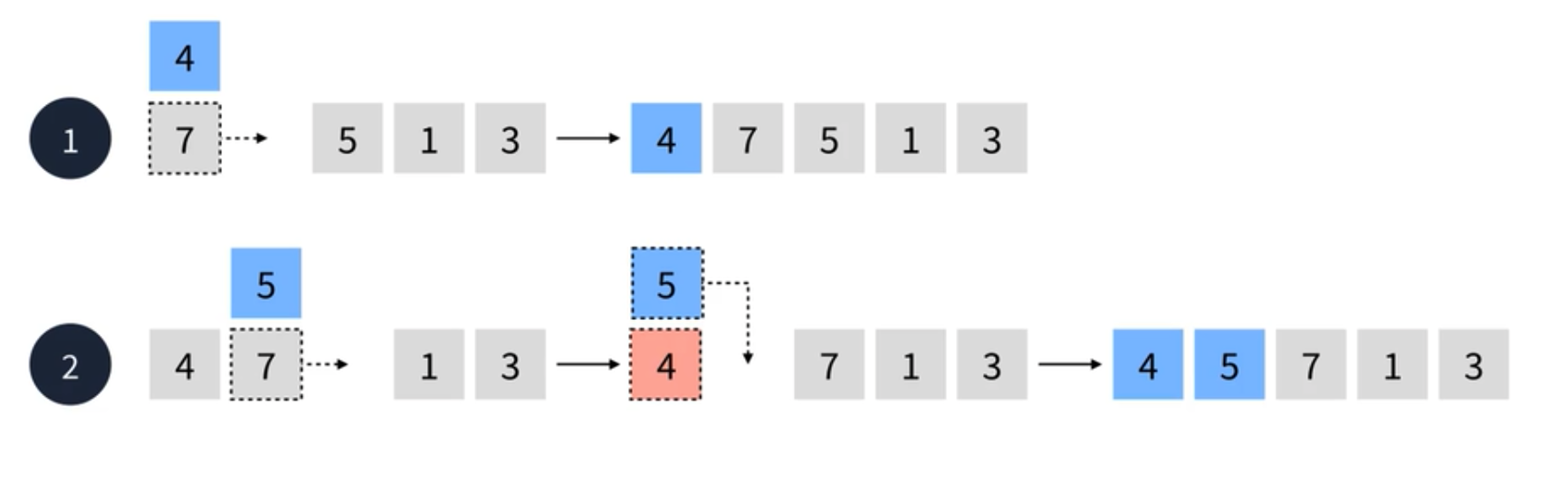
1. 삽입 정렬은 특이하게 두번째 요소부터 시작한다. 4를 선택하여 7과 비교한다. 7이 더 크기 때문에 7을 밀어내고 4가 삽입된다.
2. 7은 4보다 크기 때문에 생략한다.
3. 세번째 요소인 5를 선택한다. 5와 7을 비교해서 7이 더 크기 때문에 7을 밀어낸다.
4. 다음으로 4와 비교한다. 4가 더 작기 때문에 밀어내지 못하고 그대로 5가 두번째 삽입 되면서 종료된다.
   
5. 이번엔 4번째 요소인 1을 선택한다. 7은 1보다 크기 때문에 밀려난다. 다음으로 5와 비교한 후 또 밀려난다. 4도 밀려나고 제일 첫번째로 1이 삽입된다.
6. 마지막 순회로 다섯 번째 요소 3이 선택된다. 7과 비교 후에 밀어내고 5와 비교 후에 밀어내고 4와 비교 후 밀어낸다. 마지막으로 1과 비교 했을 때 더 이상 밀어낼 수 없으므로 그대로 두번째에 삽입이 된다.
   삽입 정렬은 이렇게 복잡하지만 어느 정도 정렬이 되어 있다는 가정하에서는 퀵 정렬보다도 빠른 성능을 보여준다.

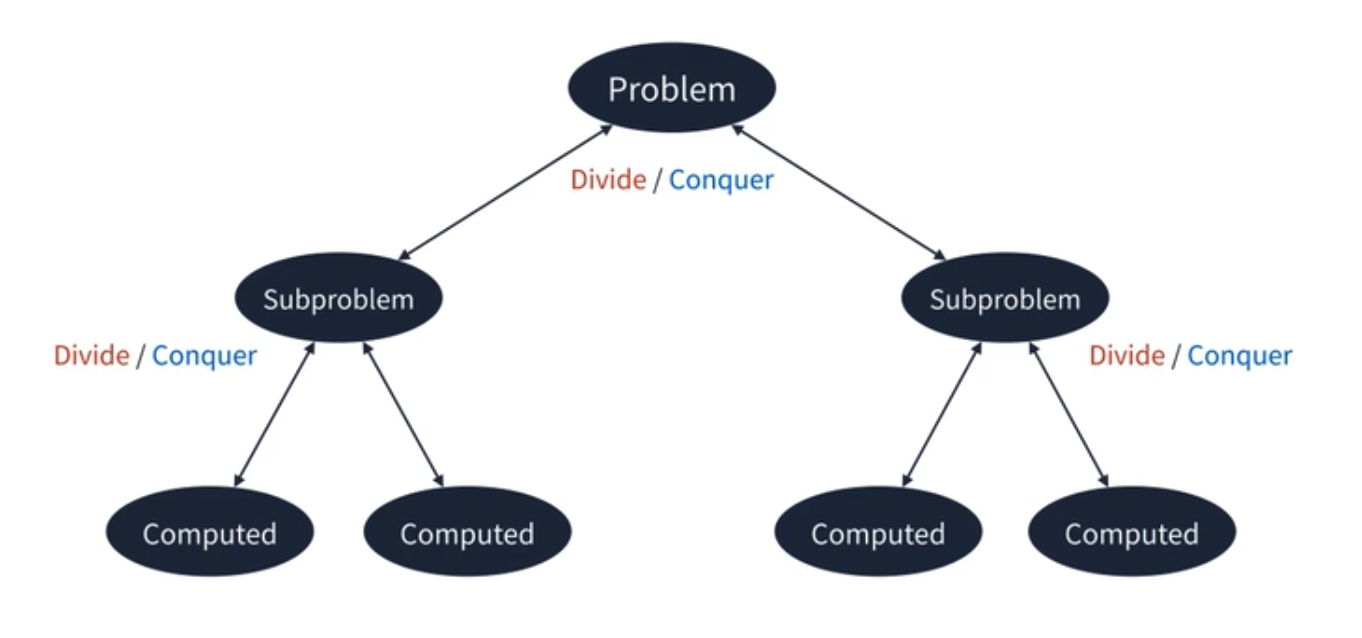
분할 정복

문제를 작은 2개의 문제로 분리하고 더 이상 분리가 불가능 할 때 처리한 후 문제를 합치는 전략이다. 꼭 분산식 전략이 아니더라도 분할 정복은 다양한 알고리즘에 응용되는 전략이니 기억에 두면 좋다.

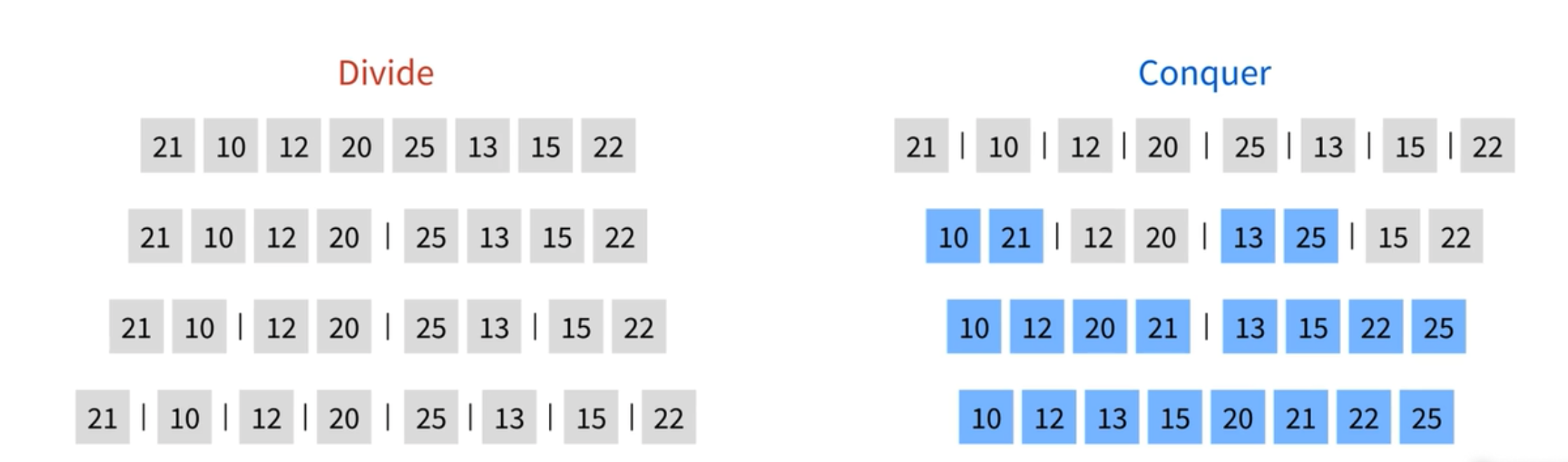
합병 정렬

분할 정복 알고리즘을 이용한 가장 정직한 알고리즘이라 할 수 있다. 정직하게 요소를 이분하여 계산하기 때문에 최악과 최선이 항상 선형 로그 시간 O(n log n) 이 걸리는 안정적인 정렬 알고리즘이다. 합병 정렬은 우선 요소들을 나누는 작업부터 시작한다. 아래의 그림처럼 우선 8개 요소를 절반으로 나눈다. 그리고 요소가 하나만 남을 때까지 계속해서 절반으로 나눈다. 모든 요소를 나눴다면 합치는 알고리즘이 진행된다. 나눈 것을 합치면 두 요소 중 작은 것을 먼저 배치한다. 예를 들어, 21 과 10 의 경우 10이 먼저 배치되고 21이 배치된다. 이어서 두개 짜리를 합칠 때도 작은 순으로 배치한다. 이 작업들은 선형 시간이 소요된다. 최종적으로 나머지를 합치면 정렬된 상태가 된다. 선형 시간이 O(log n) 만큼 걸려서 O(n log n) 시간 복잡도가 소요된다.

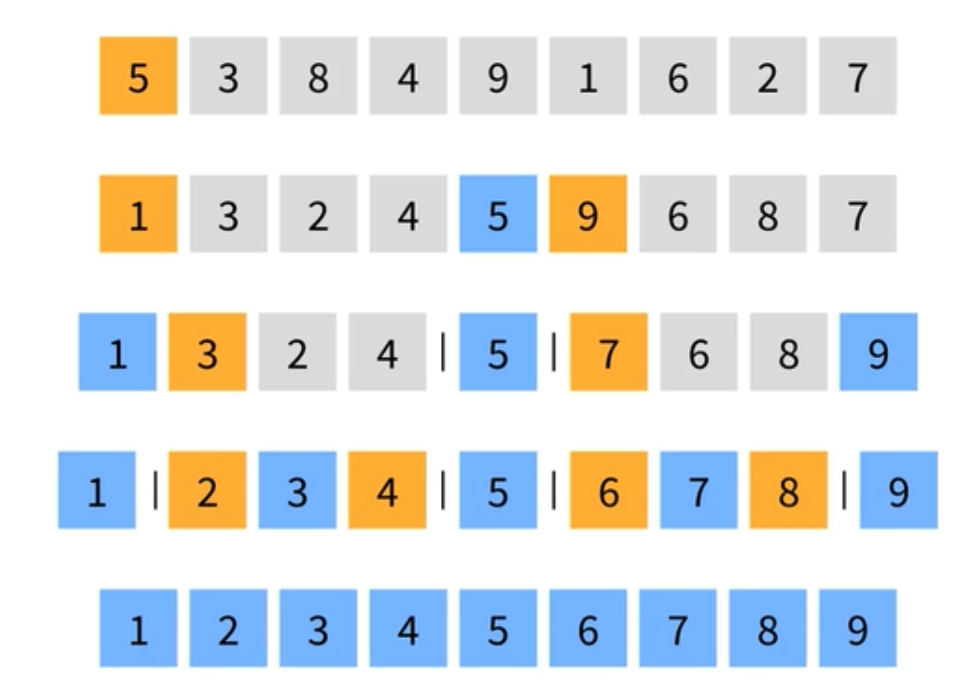
퀵 정렬

퀵 이라는 이름이 붙을 정도로 평균적으로 빠른 성능을 보여준다. 하지만 특정 경우엔 이차 시간이 걸리는 최악의 경우가 존재한다. 그래서 퀵 정렬은 불안정 정렬이라고 부른다. 시간 복잡도는 합병 정렬과 같은 선형 로그 시간이다. 퀵 정렬은 피벗이라는 기준으로 좌측과 우측을 나눈다. 여기서는 첫번째 요소인 5를 피벗이라 치고 진행하면 5를 기준으로 작은 값을 왼쪽에 배치, 큰 값이 오른쪽에 배치된다. 그리고 다시 나눈 배열에서 첫번째 요소가 피벗이 된다. 각각 1과 9인데 이 숫자를 기준으로 나뉜다. 이번엔 전부 큰 값과 작은 값으로 나뉠 수 있다. 다시 첫번째 요소들이 피벗이 된다. 이렇게 마지막으로 더 이상 나눌 수 없는 상태가 되었다면 그대로 합쳐준다. 그럼 요소들이 정렬된 상태로 나열된다.