Markov Decision Process

Markov Decision Processes(MDP)

• MDP는 강화학습에서 환경을 설명한다. 환경은 fully observable하고, 대부분의 RL problems는 MDP로 표현할 수 있다. optimal control(최상의 정책 만들기)은 MDP로 제어하고, Partially observable problems도 MDP로 변환할 수 있다.

Markov Property

• "현재가 주어진 상황에서, 미래는 과거와 무관하다"
• 각 상황은 해당 상황의 history의 관련 정보를 담고 있다. state 그 자체만으로 과거의 기록들이 내포되어 있는 것이기 때문에 과거의 정보를 따로 사용하지는 않는다.
• A state $S_t$는 Markov이다 if and only if
  $\mathbb{P}[S_{t+1} | S_t] = \mathbb{P}[S_{t+1} | S_1, \dots, S_t]$
  

State Transition Matrix

• Markov state s와 successor state(다음에 도달하게 될 상태) s'에서, state transition probability는 다음과 같이 정의된다.
  $\mathcal{P}_{ss'} = \mathbb{P}[S_{t+1} = s' | S_t = s]$
• state transition matrix P에서는 모든 state에서 모든 successor states s'가 발생할 확률을 나타낸다. 각 row를 합치면 1이 된다.
  $\mathcal{P} = \begin{bmatrix} \mathcal{P}_{11} & \cdots & \mathcal{P}_{1n} \\ \vdots & \ddots & \vdots \\ \mathcal{P}_{n1} & \cdots & \mathcal{P}_{nn} \end{bmatrix}$

Markov Process

• 기억이 없는 무작위 과정 : 현재 상태가 미래 상태에 대한 모든 중요 정보를 포함하고 있음을 의미함. 즉 미래 상태는 현재 상태에만 의존하며 과거 상태는 중요하지 않음
• Sequence of random states : Mervoc Process에서는 상태가 무작위로 전이된다. 상태들은 시간이 지남에 따라 변화하며, 각 상태의 전이는 특정 확률로 결정된다.
• Markov property : 현재 상태가 미래 상태에 영향을 미치는 유일한 정보로, 과거 상태를 따로 고려하지 않는다.

Example : Student Markov Chain Episode

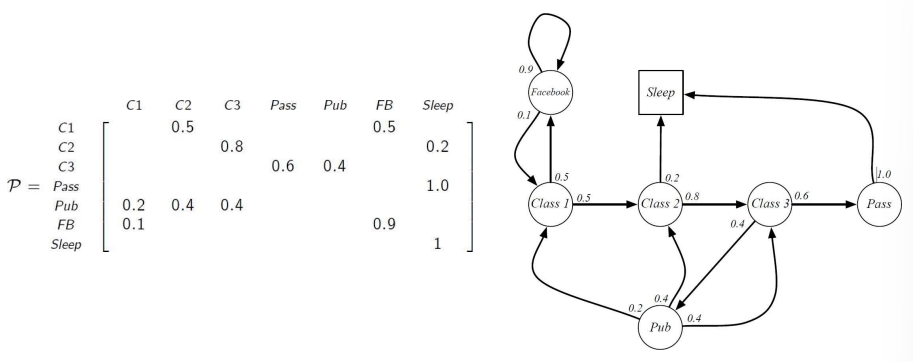
학생이 각 상태에서 다른 상태로 전이될 확률 표는 다음과 같이 표현된다. 각 상태에서 다른 상태로 넘어갈 때, 오직 전이 matrix P를 참조하여(현재 상태만을 참조하여) 다음에 등장할 state가 결정된다.

Markov Reward Process

• Markov chain을 확장한 것으로 , 각 상태 전이에 보상 값이 추가된 형태임.
• Markov Reward Process는 tuple로 정의 : $\langle S,P,R,\gamma \rangle$
  - $S$ 는 state의 유한한 set이다.
  - $P$ 는 state transition matrix임.
  - $R$ 은 reward function임: $R_s = \mathbb{E}[R_{t+1} \mid S_t = s]$
  - $\gamma$ 는 discount factor로 0과 1 사이의 값임.
  
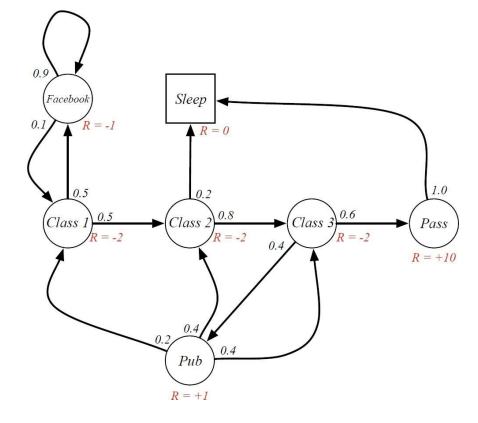
  다음과 같이, 다른 상태로 전이될 확률 뿐만 아니라 reward 또한 포함한다.

(Discounted) Return

$G_t = R_{t+1} + \gamma R_{t+2} + \ldots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$

• return $G_t$는 time-step $t$부터의 discount된 reward의 통합이다. $G_t$는 일반적인 reward와 달리 시간이 지남에 따라 미래의 reward의 값이 절감되어 돌아온다.
• discount value $\gamma$ 는 미래의 보상에 대한 현재의 가치를 뜻한다. 즉 미래의 가치를 얼마나 쳐줄 지!에 대한 value이다.
• $\gamma$는 미래의(지연된) 보상보다 현재의 보상을 더 높게 쳐준다.
  - $\gamma$가 0에 가까우면 근시안적(myopic)으로 평가함
  • $\gamma$가 1에 가까우면 미래지향적(far-sighted)으로 평가함.

Why discount?

• 대부분의 Markov reward와 dicision process는 discount된다. Why?
  - 순환적인 Markov process에서 미래의 reward에 대해 discount를 하지 않으면 무한 루프에 빠질 수 있음. 미래의 reward에 대해 discount를 적용해야 이를 방지 가능함.
  • 미래의 불확실성 : 미래는 불확실하고, 시간이 지남에 따라 불확실성은 점점 더 커짐. 따라서 보다 가까운 미래의 보상을 더 중요하게 평가함.
  • 금융 보상의 시간 가치 : 금융 문제의 경우, 자금을 현재 사용하는 것이 미래에 사용하는 것보다 가치가 높음
  • 동물과 인간의 즉각적인 보상 선호 : 실험심리학에서 애초에 동물이랑 인간이 즉각적인 보상을 더 선호한다는 결과가 나왓음!
• discount 없는 Markov 보상 과정 사용 가능성 : 모든 에피소드가 종료되어 무한대로 진행되지 않는다는 상황 하에 discount를 1로 설정(즉 discount가 걍 없음)할 수 있음.

Value Function

• value function $V(s)$는 state s에 대해 long-term value를 출력한다. 즉 discount를 포함한 value를 출력한다.
• $v(s) = \mathbb{E}[G_t \mid S_t = s]$
  
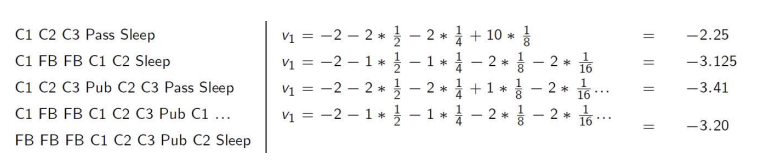
  다음과 같이, 미래의 보상에 대해서 discount가 곱해져 $G_t$가 정해진다.

Bellman Equation for MRPs

• value function은 두 파트로 쪼개질 수 있음:
  - 즉각적인 보상 $R_{t+1}$
  - succesor state $\gamma v(S_{t+1})$의 discounted된 value
  $\begin{aligned} v(s) &= \mathbb{E}[G_t \mid S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldots \mid S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + \ldots) \mid S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma G_{t+1} \mid S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma v(S_{t+1}) \mid S_t = s] \end{aligned}$
• 다음과 같이 설명할 수도 있음 : $v(s) = R_s + \gamma \sum_{s' \in S} P_{ss'} v(s')$
  여기서 $\sum_{s' \in S} P_{ss'} v(s')$가 잘 이해가 안됐는데, 이 부분은 state s에서 만약 A, B, C 상태 중 하나로 전이 가능할 때, $(P_{sa} V(a) + P_{sb} V(b) + P_{sc} V(c))$를 뜻한다. 여기서 P는 다른 상태로의 전이 확률, V는 해당 상태의 value를 뜻한다.(discount 생략)
  
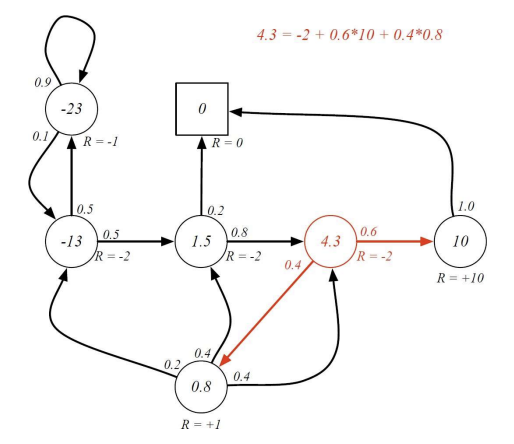
  이러한 Bellman Equation에 따라 각 state의 value는 다음과 같이 계산된다.

Bellman Equation in Matrix Form

Bellman Equation은 matrix로 표현할 수도 있다.
$V = R + \gamma PV$

Solving the Bellman Equation

Bellman 방정식을 어떻게 푸는지 / state의 value를 어떻게 계산하는지

• Bellman Equation은 선형 방정식이다.
• Direct Solution (직접 해법)
  - N state에 대한 계산 복잡도는 $O(N3)$
  • 따라서 state가 많아지면 직접 해법을 사용하는 것이 매우 비효율적이거나 불가능하므로, 작은 MRP에만 적합함.
• 큰 MRP에 대한 반복적인 방법
  - 위에서 말한 대로, 큰 규모의 MRP에서는 벨만 방정식을 직접 풀기 어려우므로, 반복적 방법을 사용하여 푼다.
  • Dynamic programming / Monte-Carlo evaluation / Temporal-Difference learning

Markov Decision Process

• vs MRP : MRP는 state와 reward만을 고려한다. 따로 decision, 즉 action을 내리는 부분이 없고 단순히 상태에서 다른 상태로 전이하면서 보상을 받는다. MDP는 MRP에서 추가적으로 action을 고려하여, 각 상태에서 여러 행동 중 하나를 고름에 따라 상태 전이 확률과 보상이 달라진다.

• 모든 state가 Markov한 상황인 environment임.

• Markov Decision Process : $<S, A, P, R, \gamma >$
  - $S$ : states의 유한한 set

  • $A$ : actions의 유한한 set
  • $P$ : 상태 전이 매트릭스
  • $R$ : reward function
  • $\gamma$ : discount factor

Policies

• policy $\pi$ 는 주어진 상태에서 어떤 행동을 할지에 대한 확률 분포를 정의한다.
  $\pi (a|s) = P(A_t=a|S_t=s$
• 즉 현재 상태 s에 있을 때 행동 a를 선택할 확률을 나타냄. agent의 의사결정 규칙.
• MDP 의 policy는 현재 상태에 기반함. (Markov랑 같음. 과거 신경 X)
• Policies는 stationary(시간과 독립적)하다. 시간에 의존하지 않고 항상 동일하게 작동함.
  $A_t \sim \pi(\cdot \mid S_t), \forall t > 0$
• MDP와 정책의 정의
  - MDP는 다음과 같이 정의됨 : $<S,A,P,R,\gamma >$
  • 이 MDP와 함께 주어진 policy는 특정 상태에서 어떤 행동을 선택할 확률을 정의하는 함수임.
• 상태 시퀀스는 Markov Process이다.
  - 주어진 policy 하에서 상태 시퀀스 $S_1, S_2, ...$는 Markov 과정 $< S,P_\pi>$를 형성함.
  • $P_\pi$는 policy가 반영된 상태 전이 확률임.
• 상태와 보상 시퀀스는 Markov Reward Process이다.
  - 상태 시퀀스와 보상 시퀀스 $S_1,R_2, S_2, ...$는 MRP $<S,A,P_\pi,R_\pi,\gamma>$를 형성함.
  • policy가 있는 상태에서 보상과 상태의 전이 과정을 다룸.
• 정책에 따른 상태 전이 확률과 보상함수
  - $P_\pi$(정책 하의 상태 전이 확률): $P_\pi(s, s') = \sum_{a \in A} \pi(a \mid s) P^a_{ss'}$
  • $P^a_{ss'}$는 상태 s에서 행동 a를 선택했을 때 다음 상태가 s'로 전이될 확률임.
  • 상태 s에서 가능한 모든 행동 a에 대한 가중합을 구하는 방식으로, 각 행동을 선택할 확률 $\pi(a \mid s)$와 그 행동으로 인해 상태 s'로 전이될 확률 $P^a_{ss'}$를 곱한 값을 확산하는 방식.
  • $R_\pi$(정책 하의 보상함수) : $R_\pi(s) = \sum_{a \in A} \pi(a \mid s) R^a_s$
  • $R^a_s$는 상태 s에서 행동 a를 선택했을 때 받는 보상임.
  • 상태 s에서 가능한 모든 행동에 대해, 각 행동을 선택할 확률과 그 행동으로 인해 받을 보상을 곱한 값을 합산한 것임.

• vs state transition matrix
  policy : 에이전트가 어떤 행동을 선택할지를 결정하는 규칙으로, 현재 상태에서 선택할 행동의 확률을 제공하며 에이전트가 학습을 하며 최적화할 수 있음.
  state transition matrix : 선택된 행동 후에 환경이 어떻게 반응할 지를 설명. 현재 상태와 행동에 따른 다음 상태로의 전이 확률을 제공함. 환경에 의해 결정되는 것으로, 에이전트가 직접 제어할 수 없음. 걍 환경의 규칙같은 거임. 정해진 사실.

Value Function

• MDP의 state-value 함수 $v_\pi(s)$는 policy를 따라 state s에서 시작하면 기대되는 return 값임.
  $v_\pi(s) = \mathbb{E}_\pi \left[ G_t \mid S_t = s \right]$
• action-value 함수 $q_\pi(s,a)$는 policy를 따라 state s에서 시작하여, action a를 했을때 기대되는 return 값임.
  $q_\pi(s, a) = \mathbb{E}_\pi \left[ G_t \mid S_t = s, A_t = a \right]$
  

Bellman Expectation Equation

• state-value function은 즉각적 보상 + succesor state의 discount된 value로 쪼개질 수 있다.
  $v_\pi(s) = \mathbb{E}_\pi \left[ R_{t+1} + \gamma v_\pi(S_{t+1}) \mid S_t = s \right]$
• action-value function도 유사하게 쪼개진다.
  $q_\pi(s, a) = \mathbb{E}_\pi \left[ R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) \mid S_t = s, A_t = a \right]$
  

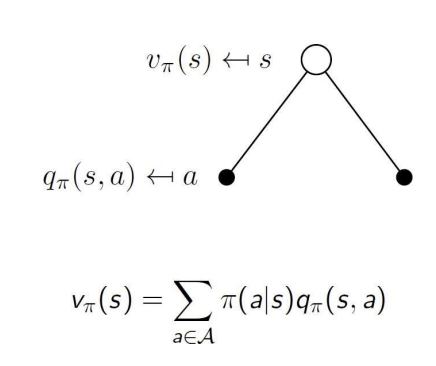
• $v_\pi(s)$는 특정 state에서의 예상 보상 값이다. $q_\pi(s,a)$는 여기서 더 나아가, 특정 state에서 행동 a를 택했을 때의 예상 보상 값이다.
• state-value function $v_\pi(s)$는 다음과 같이, 특정 state에서 행동 a를 선택할 확률 곱하기 특정 state에서 행동 a를 선택했을 때의 가치인 action-value function $q_\pi(s,a)$ 로 표현할 수 있다.

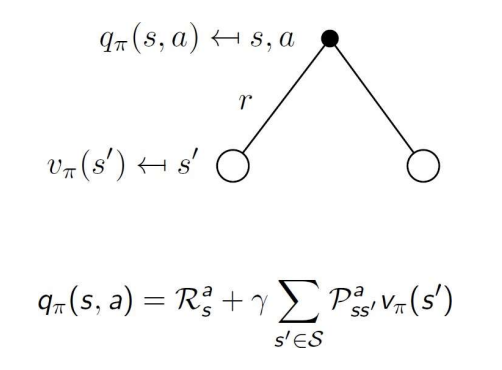
• $q_\pi(s,a)$ 는 state s에서 행동 a를 했을 때의 예상 보상 값이다. 이 값은 그림에서와 같이 a를 행함으로써 보상 r과 전이되는 state s'에서의 value를 더한 값과 같다.
• action-value function $q_\pi(s,a)$는 다음과 같이, a를 행함으로써 얻는 즉각적인 보상 $R^a_s$와 s에서 a를 행함으로써 발생할 수 있는 s'의 확률과 s'에서의 value를 곱한 값인 $P^a_ss' v_\pi (s')$에 discount value를 적용하여 표현할 수 있다.

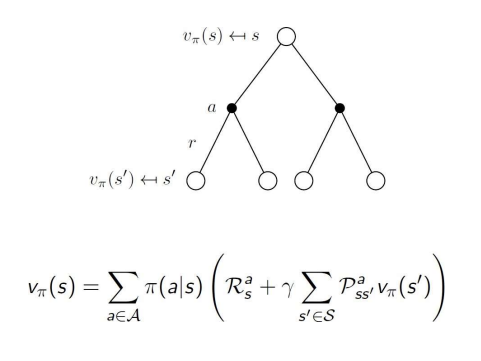
• $v_\pi$는 다음과 같이 표현된다 :
  시그마
  - state s에서 policy에 따라 행할 수 action의 확률
  곱하기
  • s에서 a를 행할 때 발생하는 즉각적인 보상 + (s에서 a를 행함으로써 s'로 전이될 확률 곱하기 전이된 s'에서의 value)

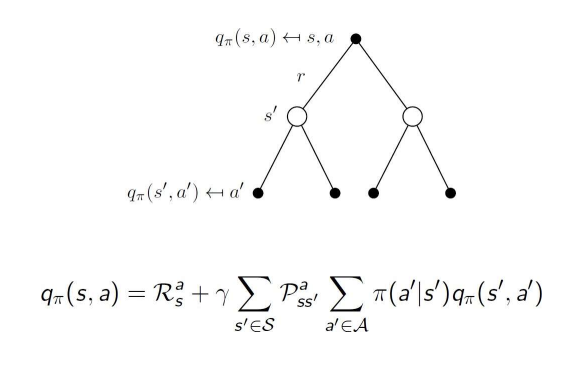
악제발그만해

• $q_\pi (s,a)$ 는 다음과 같이 표현된다 :
  - s에서 a를 행할 때 발생하는 즉각적인 보상
  더하기
  discount value * 시그마
  • s에서 a를 행함으로써 s'로 전이될 확률
    곱하기 시그마
  • policy에 따라 s'에서 특정 행동 a'를 행할 확률
    곱하기
  • policy에 따라 s'에서 a'를 행할 때의 value

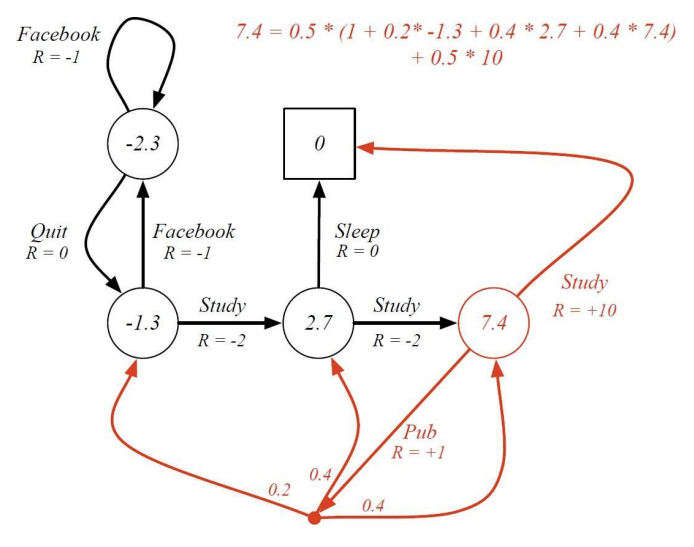
example

Bellman Expectation Equation in Matrix Form

• Bellman Expectation Equation은 matrix를 통해 표현할 수 있다.

$V_\pi = R_\pi + \gamma P_\pi V_\pi$
$V_\pi = (I - \gamma P_\pi)^{-1} R_\pi$

여기까지의 쟁점!!

• 목표는 누적된 보상을 최대화시키는 것!
• optimal policy는 어떻게 찾는가?
• 어떤 policy가 더 좋은지 어떻게 결정하는가?

Optimal Value Function

• optimal value function은 MDP의 환경에서, 모든 정책 중에서 가장 높은 기대 보상을 제공하는 가치 함수임.

• MDP를 solve한다는 것은 optimal value function을 아는 것을 의미. optimal value function을 안다면 에이전트는 어떤 상태에서 어떤 행동을 해야 최대의 보상을 받을 수 있을지 알 수 있기 때문에 중요함.

• optimal state-value function : $v_{*}(s)$는 주어진 state s에서 에이전트가 받을 수 있는 최대의 기대 보상을 나타냄. 즉 모든 정책 중에서 최적의 정책을 사용했을 때의 기대 보상을 말함.
  $v_*(s) = \max_\pi v_\pi(s)$

• optimal action-value function : $q_*(s, a)$는 state s에서 a를 행할 때 에이전트가 받을 수 있는 최대의 기대 보상을 나타냄. 즉, 모든 정책 중에서 최적의 정책을 사용했을 때의 기대 보상을 말함.
  $q_*(s, a) = \max_\pi q_\pi(s, a)$
  

Optimal Policy

• $\pi$의 기대 보상이 $\pi'$보다 크거나 같을 때, $\pi$가 $\pi '$보다 더 좋거나 같은 수준의 정책이라고 할 수 있다.
  $\pi \geq \pi' \ \text{if} \ v_\pi(s) \geq v_{\pi'}(s), \ \forall s$
• 모든 MDP에 대해서 다음과 같은 규칙들이 성립한다 :
  - optimal policy $\pi_{*}$이 존재할 때, 이 policy는 다른 모든 policy들보다 좋거나 동일하다.
  • 모든 optimal policy들은 optimal value function을 얻는다. 즉, 모든 optimal policy는 가능한 가장 많은 value를 도출한다.
    $v_{\pi_{*}}(s) = v_{*}(s)$
  • 모든 optimal policy는 optimal action-value function을 얻는다. 즉, 모든 optimal policy는 최적의 action을 선택하여 가능한 가장 많은 value를 도출한다.

Finding an Optimal Policy

• optimal policy는 $q_{*}(s,a)$를 최대화함으로써 찾을 수 있다.
  $\pi_*(a \mid s) = \begin{cases} 1 & \text{if } a = \arg\max\limits_{a \in A} q_*(s, a) \\ 0 & \text{otherwise} \end{cases}$
• 모든 MDP에 대해 항상 deterministic optimal policy가 존재한다.(최선의 action 선택을 통한 최대의 value 창출)
• 우리가 $q_{*}(s,a)$, 가장 큰 값을 내는 action-value function을 안다면, 우리는 바로 optimal policy를 얻는 것

Bellman Optimality Equations for $$q_{*}

optimal value function은 Bellman optimality equation을 통해 재귀적으로 정의된다.

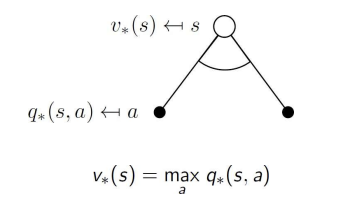
다음과 같이, v는 q에서 value가 max가 되는 행동을 고르는 것으로 정의된다.

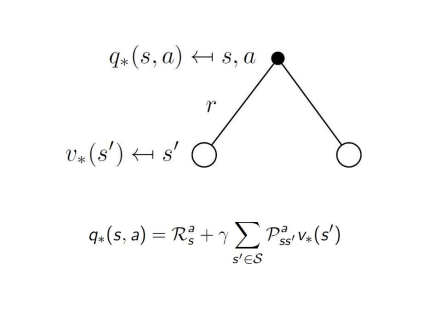
q는 행동을 선택했을 때 발생하는 즉각적인 reward와 시그마(a를 택함으로써 전이되는 s'의 확률*상태 s'에서의 최적의 value)로 정의할 수 있다.

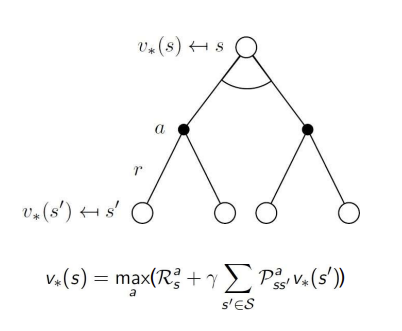
즉 처음의 v가 q로 정의되었던 것, 그리고 두번째의 q가 다시 v로 정의되는 것을 연결하면 다음과 같이 v로 정의된 q로 정의된다..

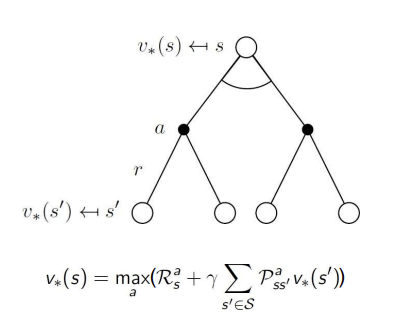
그리고... v가 다시 q로 정의되었듯이 q는 또 q로 정의된 v로 정의된다. ...
제발 그만해

Solving the Bellman Optimality Equation

• Bellman Optimality Equation은 비선형이다. 상태와 행동의 선택이 상호작용하며 단순한 선형 연산으로는 해결되지 않는다.
• 일반적으로 닫힌 해가 없다, 즉 방정식을 명시적으로 풀어서 간단한 수식으로 표현을 할 수 없는 경우가 많음. 때문에 반복적인 방법을 통해 점진적으로 해를 구하는 방식이 필요하다.
• iterative solution method : 반복적인 방법을 사용하여 해결. 대표적으로 policy iteration과 value iteration

Bellman Expectation Equation vs Bellman Optimality Equaition

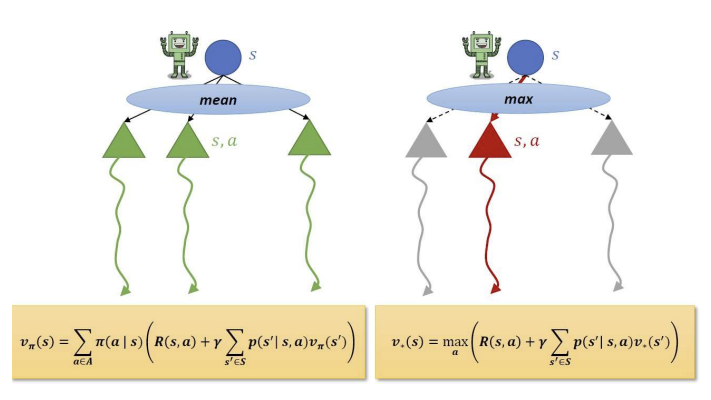
• Bellman Expectation Equation은 policy 하의 가치 함수를 계산하는 계산하는 방식으로, 기대값(mean)을 사용한다. 즉 주어진 상태에서 각 행동을 취할 확률에 기반하여 여러 행동의 평균을 취하는 방식이다.
  --> 즉 얘는 그냥 state s의 기댓값
• Bellman Optimality Equaition은 최적 정책에 대한 최적 가치 함수를 계산하는 방식으로 최대값(max)를 사용한다. 즉 상태 s에서 가능한 행동들 중 가장 최적의 행동을 선택하여 최댓값을 취한다.
  --> 즉 얘는 그냥 state s의 최댓값