Model-based Planning

Planning and Learning

• sequential decision making의 two problems
• Planning :
  - environment의 model이 알려져 있음
  • 외적인 상호작용 없이 agent가 model을 통해 계산을 진행한다. 즉 에이전트가 직접 환경과 상호작용하지 않는다.
  • 에이전트는 현재 정책을 사용해 환경 내에서 가능한 시나리오들을 시뮬레이션하고, 이를 통해 각 상태에서의 value를 계산하고 상태와 행동의 결과를 예측한다.
  • 이러한 방식으로 계산된 value를 바탕으로 정책을 점진적으로 개선한다. 이 과정은 Dynamic Programming이나 policy iteration, value iteration과 같은 기법을 통해 이뤄질 수 있음

What is Dynamic Programming?

• 복잡한 problem을 더 단순한 sub-problem으로 재귀적으로 분할하여 단순화 시키는 방식!
  - sub-problem을 푼다.
  • sub-problem들을 final solution으로 결합한다.

Requirements for Dynamic Programming

• DP가 적용될 수 있는 문제의 두 가지 주요 속성:
  - Optimal substructure(최적 부분 구조)
  - 문제를 작은 하위 문제로 나눌 수 있는 특성을 말함. 즉큰 문제를 해결하려면 그 문제의 부분 문제를 최적으로 해결 할 수 있어야 함. 그리고 부분 문제의 최적 해결 방법을 이용해 전체 문제의 최적 해결 방법을 구할 수 있음
  - principle of Optimality : 최적성의 원리로, 최적의 해결 방법은 부분 문제의 최적 해결 방법을 포함함.
  - Optimal Solution Decomposition : 최적의 해결 방법을 작은 하위 문제들로 분해할 수 있음
  • Overlapping subproblems(중복되는 하위 문제)
    • 중복되는 하위 문제는 동일한 하위 문제가 여러 번 반복해서 등장하는 특성을 말함.
      • DP에서는 이러한 중복되는 하위 문제의 해를 캐싱(데이터나 계산 결과를 미리 저장)하거나 재사용하여 동일한 계산을 여러 번 하는 것을 방지함.
      • 즉, 한 번 해결한 하위 문제의 해를 저장하고, 필요할 때 다시 불러와서 시간을 절약할 수 있음.
  • MDP는 이 두 가지 속성을 모두 만족함
    • Bellman Equation : MDP를 재귀적으로 분해할 수 있게 해줌(Optimal substructure)
      • value function : 한 번 계산된 상태의 가치를 저장하고 재사용할 수 있음. (Overlapping subproblems)

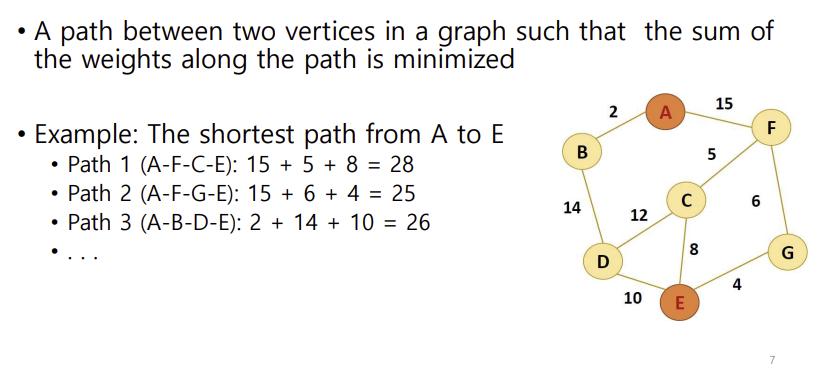
예시임. 한 번 갔던 길은 저장해서 또 써먹음

Planning by Dynamic Programming

• MDP의 모든 정보가 주어졌을 때 사용됨
  DP는 MDP의 상태, 행동, 보상, 상태 전이 확률을 모두 알고 있을 때 사용할 수 있는 방법으로, Planning 태스크에 사용되며 에이전트가 미래 행동을 결정하는 데에 도움이 된다.
• For Prediction(주어진 정책 하에서 각 상태의 가치함수를 계산하는 과정)
  - input : MDP $<S,A,P,R,\gamma >$와 정책 $\pi$
  • output : 정책 하에서의 가치함수 $v_{\pi}$(즉 정책에 따라 각 상태에서 예측되는 누적보상)
• For Control(최적의 정책과 최적의 가치 함수를 찾는 과정)
  - input : MDP $<S,A,P,R,\gamma >$
  • output : 최적의 가치함수 $v_*$와 최적의 정책 $\pi_*$
  • 최적의 가치함수를 찾아내면 최적의 정책 또한 찾을 수 있음.
  • 최적의 정책을 찾아내어 각 상태에서 가장 높은 보상을 얻을 수 있는 정책을 학습하는 것

Iterative Policy Evaluation

• 주어진 정책 $\pi$를 어떻게 평가하는가
  - Bellman expectation backup을 통해 반복적인 계산
  *Bellman Expectation backup? 밸만 기대 방정식을 기반으로 가치함수나 행동 가치 함수를 업데이트하는 과정. 주어진 정책에 따라 기대값을 계산하고 그 값을 이용해 가치 함수의 값을 백업하는 방식
• 각 iteration(반복횟수) k+1에 대해
• 모든 state에 대하여
• $v_k (s')$로부터 $v_{k+1}(s)$를 업데이트한다.
  $v_{k+1}(s) = \mathbb{E}_\pi \left[ R_{t+1} + \gamma v_k(S_{t+1}) \mid S_t = s \right] v_{k+1}(s) = \sum_{a} \pi(a \mid s) \sum_{s', r} p(s', r \mid s, a) \left[ r + \gamma v_k(s') \right]$
• $v_k$를 계속해서 update하면 $v_\pi$에 수렴하게 된다.

Example : small grid world

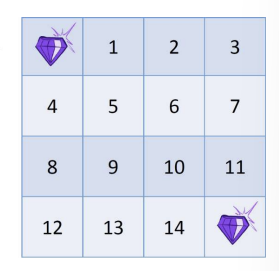
• discount value : 1 (할인 없음)
• Nonterminal states 1,...,14
• grid를 나가는 action을 할 때 state가 변하지 않음(1에서 위로 가면 state가 걍 1 그대로인 너낌)
• 모든 이동에 대해 reward는 -1

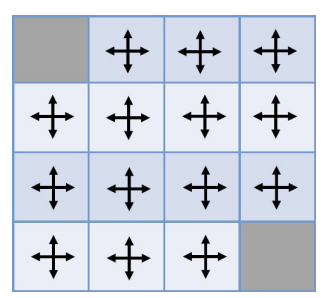
policy : 동일한 랜덤 policy를 따름
$\pi(n \mid \cdot) = \pi(e \mid \cdot) = \pi(s \mid \cdot) = \pi(w \mid \cdot) = 0.25$
즉 그냥 똑같은 확률로 랜덤하게 움직임

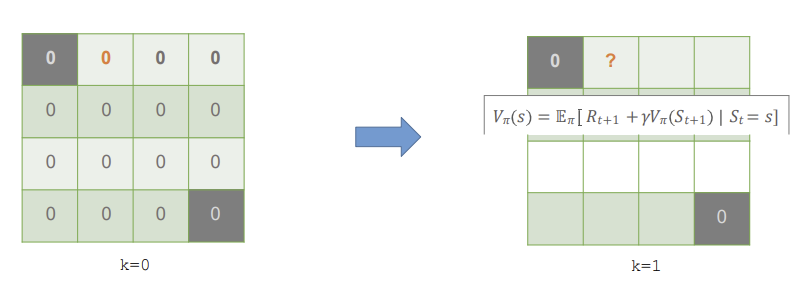
k=0, 즉 완전 초기 상태로, 모든 상태의 초기값을 0으로 세팅함.
이제 k=1, 첫 번째 반복 시작! 각 state의 value를 구해보자
먼저, 1 state의 value를 계산해보자.

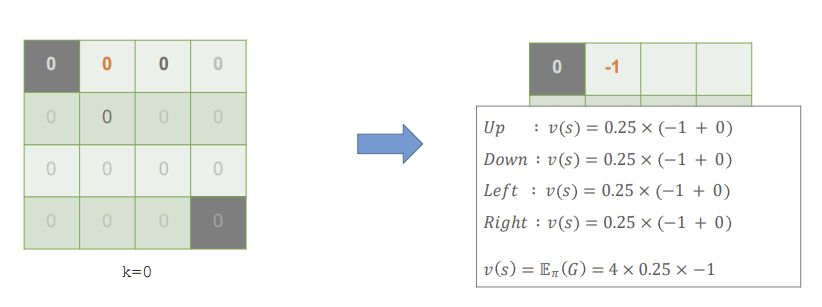
action으로는 up, down, left, right가 있다. 그리고 각각의 action이 행해질 확률은 모두 0.25이다.
up의 경우를 중점적으로 보자면, 행해질 확률인 0.25 * (즉각적인 reward -1 + up을 했을 때의 state의 value 0)으로 -0.25의 값이 나온다. 아직 모든 state의 value가 0이므로 모든 액션에 대해 똑같이 작용되어 value가 -1이 된다.

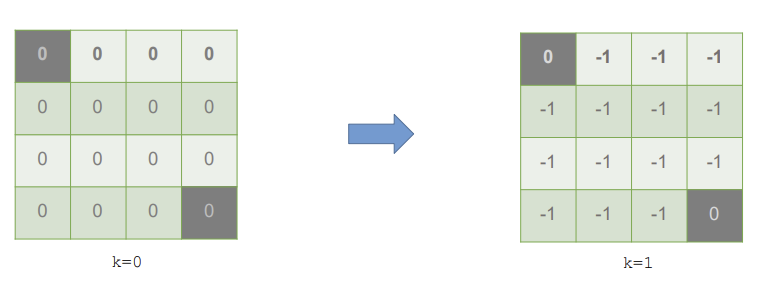
모든 state에 대해 value를 정하면 방금의 state 1과 같이 모든 state가 -1의 value를 가지게 된다.

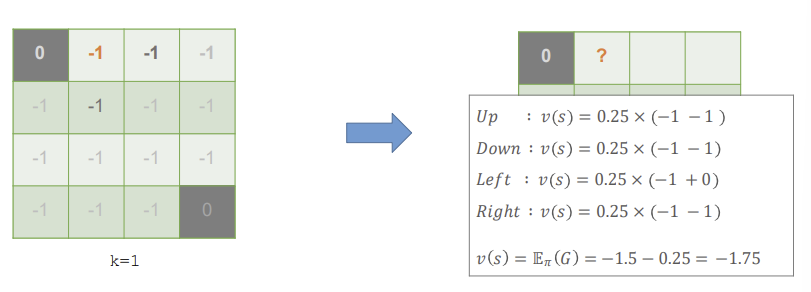
이제 두번째 iteration을 해보자. 마찬가지로 예시로 state 1에 대해 계산을 해보겠다.
state 1에서 up을 하게 되면, 먼저 up이 행해질 확률 0.25 * (즉각적인 reward -1 + up을 했을 때의 state의 value -1)으로 -0.5의 값이 나온다. 다음 상태로 넘어갔을 때 -1이 나오는 경우는 up, down, right이므로 이 세 가지 action에 대해서는 같은 값이 나온다. 반면 left를 행할 경우, 전이되는 state의 value가 0이 되므로 -0.25가 된다.
이러한 계산의 결과, k=2에서의 state 1의 value는 -1.75가 된다.

이러한 계산을 모든 state에 행했을 때 다음과 같은 결과가 나오게 된다.

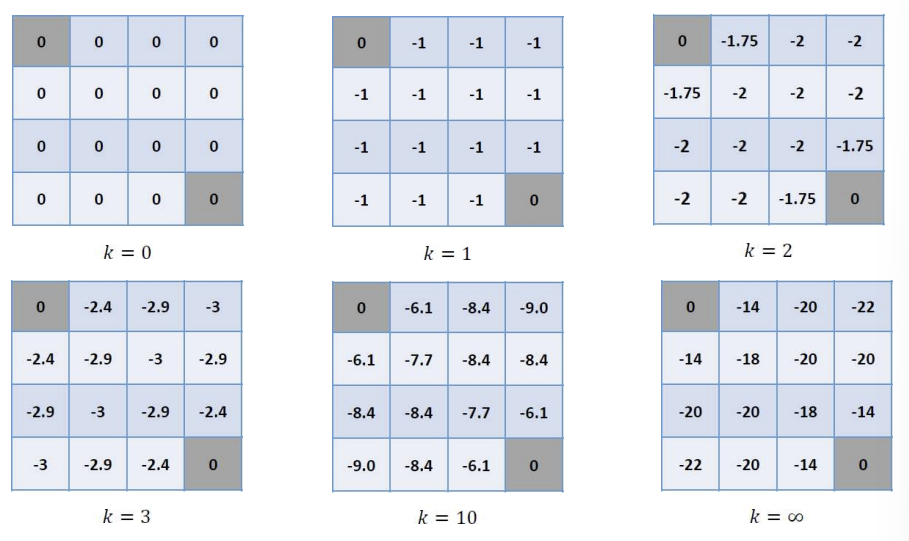
이러한 계산 방식으로 value function을 업데이트하면 k의 값(iteration 횟수)에 따라 다음과 같은 결과가 나온다.

Algorithm: Iterative Policy Evaluation

input은 $\pi$, 정책이 평가된다.
알고리즘 파라미터 : 작은 threshold $\theta$로, 업데이트를 더 할지 말지를 결정하는 값이다.
모든 state에 대해서 V(s)를 초기화한다. 종료 state에 한해서는 0으로 설정한다.

그리고 iteration k에 따라 loop를 돌린다.
변화량인 $\delta$는 0으로 초기화 한다.
모든 state에 대하여, 이전 반복에서 저장된 상태 가치 v를 저장하고, 이후 새로운 상태 가치 V(s)를 업데이트한다. V(s)에 대해서는 많이 봐 온 식이니 넘어가고,
각 상태에서의 변화량 $\delta$는 이전 가치 v와 새로운 가치 V(s) 사이의 차이 중 가장 큰 값을 선택하며, 이 값이 수렴 기준인 $theta$보다 적어질 때까지 반복한다. 변화량이 임계값보다 작아지면 알고리즘이 종료되며, 상태 가치 함수가 충분히 수렴했다는 뜻이다.

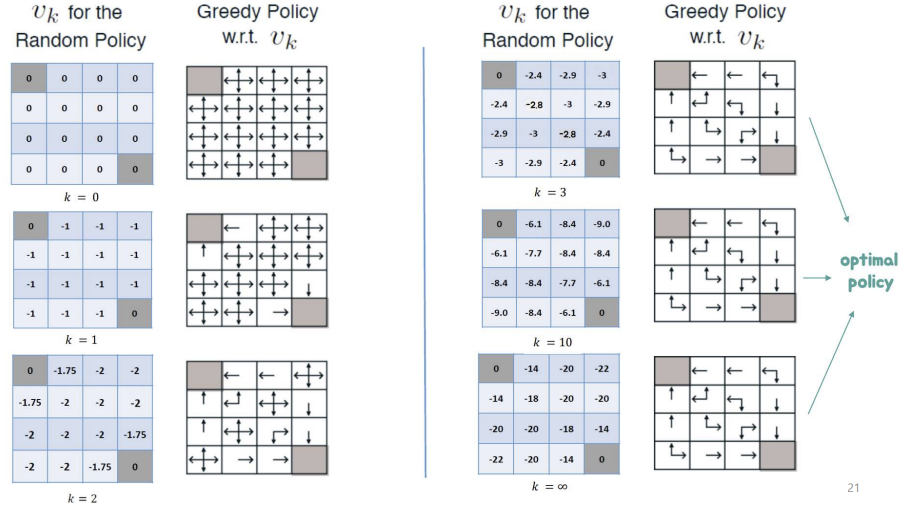
random policy(각 action의 확률이 똑같은 policy의 value를 통해 greedy하게 policy를 업데이트하면 다음과 같은 optimal policy가 도출된다. 이러한 과정을 반복하는 것!

Policy Iteration

즉 policy iteration은 evaluation과 improve의 반복으로 진행된다.

• evaluation : 앞선 small grid world의 예시와 같이, 현재의 policy에 따라서 value function을 구한다. 그 결과, 각 state의 value가 나오게 된다.
• improve : 앞선 evaluation의 결과인 $v_{\pi}$에 따라, policy를 greedy하게 개선시킨다.
  $\pi ' = greedy(v_{\pi})$
• small grid world에서는, 적은 iteration만으로도 optimal한 policy를 만들 수 있었다. 하지만 일반적인 상황에서는 더 많은 iteration이 필요하다.
• policy iteration은 항상 optimal policy $\pi^*$로 수렴된다.

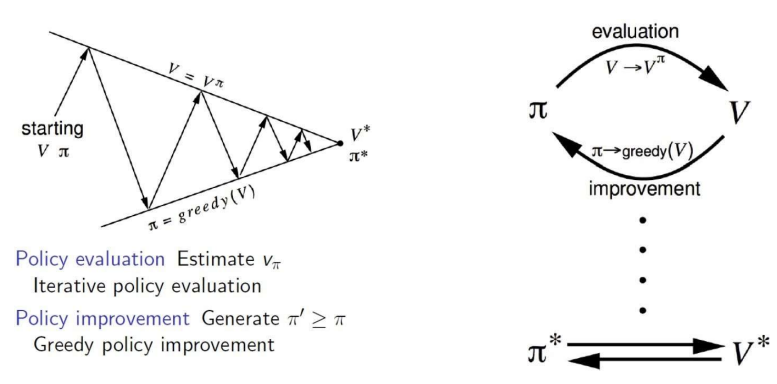
즉 이런 것이당.. evaluation을 통해 가치 함수를 측정하고, 측정된 가치함수에 따라 policy를 greedy하게 improve한다.

Policy improvement

• 특정 state에서 최선의 행동을 결정해버리는 deterministic policy의 경우, $a = \pi (s)$라고 할 수 있음.
• greedy하게 하면 policy를 개선할 수 있음.
  $q_\pi(s, \pi'(s)) = \max_{a \in A} q_\pi(s, a) \geq q_\pi(s, \pi(s)) = v_\pi(s)$
  정책에 따른 action-value function에서 state s에서의 업데이트된 policy에 따른 최선의 행동의 value = 정책에 따른 action-value function에서 state s에서 행할 수 있는 행동들의 가치의 max >= 정책에 따른 action-value function에서 s에서 이전 정책에 따른 최선의 행동의 value = 정책에 따른 state-value function의 state s에서의 가치
  너무너무 복잡하긴 한데.. 결국 하고 싶은 말은 새로운 정책 하에서 선택된 행동이 항상 이전 정책에 비해 더 높은 가치를 제공한다는 것! 즉 iteration이 더 깊어질수록 더 개선된 policy와 value function이 보장된당~~
  
• $v_{\pi'}(s) \geq v_{\pi}(s)$는 항상 보장되는가?
  예 맞습니다~ iteration을 할수록 더 policy는 이전 policy보다 성능이 좋거나 같다!!!
  
• improvement가 중단되면, Bellman optimality equation이 만족된다
  $v_\pi(s) = \max_{a \in A} q_\pi(s, a)$
• 그러므로, 모든 state에 대해 $v_{\pi}(s) = v_{*}(s)$가 성립된다. 즉, 끝까지 improve를 했을 때, 그때의 policy는 optimal 하다는 것~

Algorithm : Policy Iteration

evaluation은 앞에서 설명했으니까.. improvement 설명을 해보겠음
policy-stable은 정책이 더 이상 변경되지 않으면 반복을 종료할 수 있도록 변수를 설정한다. 이 값이 계속 true로 유지되면 정책이 안정화 되었다는 뜻!!!!
모든 state에 대하여,
old-actiond을 이전 improve의 결과인 $\pi(s)$로 업데이트한다.
그리고 이제 새롭게 $\pi(s)$를 업데이트한다.
$\pi(s) \leftarrow \arg\max_a \sum_{s', r} p(s', r \mid s, a) \left[ r + \gamma V(s') \right]$
old-action이 업데이트된 policy의 action과 다르면 policy-stable이 false로 설정한다.
만약 policy-stable이 true면 개선을 중단하고 V와 $\pi$를 return한다. false면 policy evaluation을 통해 value function을 업데이트합니다잉

Modified policy iteration

policy iteration의 다양한 방향성에 대해 고민해보장

• policy evaluation가 꼭 $v_\pi$에 수렴해야함?
• 종료조건을 도입해보는 건 어떰?
• 아니면 걍 k iteration 후에 끝내버리는건?
• policy를 매 iteration마다 업데이트하지 않는 것은? (=value iteration)

principle of optimality

optimal policy는 두 가지 요소로 나뉘어짐

• optimal first action : 주어진 상태에서 가장 처음에 행해야 할 최적의 행동
• 후속상태 s'에서의 최적 정책 : 첫번째 행동 후 도달한 s'에서 계속해서 최적 정책을 따르는 과정

Deterministic Value iteration (결정론적 가치 반복)

• subproblem $v_{*}(s')$의 해를 알고 있을 때, 상태 s에서 optimal state value $v_{*}(s)$는 한 단계 미리 보기로 다음과 같이 구할 수 있음.
• 위의 업데이트 과정을 반복적으로 적용하여 상태 가치 함수를 계산함.
• value iteration은 마지막 상태(종료 상태)와 보상을 시작점으로 하여 거꾸로 동작함. 종료 상태에서부터 가치 함수를 계산해나감.
• 즉, 먼저 종료 상태의 가치를 설정하고, 그 상태에서부터 거꾸로 가치를 계산하는 과정
• 이 방법은 stochastic MDP에서도 작동함. 상태 전이 확률이 고정되있지 않더라도, 가치 방법을 통해 최적의 상태 가치를 계산할 수 있음

Value iteration

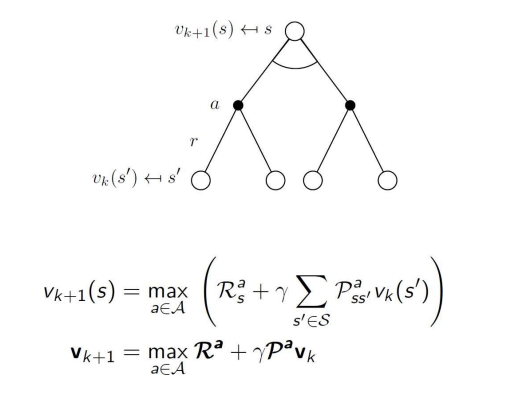
• optimal policy를 찾기 위하여~
  - policy iteration의 일종으로 policy evaluation이 한 번의 평가 과정 후에 중단되는 case
  • value iteration에서는 bellman optimality equation을 반복적으로 적용하여 최적 정책을 찾음.
• Bellman optimality backup을 반복적으로 적용
  - 각 iteartion k+1에 대해
  - 모든 state에 대해
  - $v_{k}(s')$를 바탕으로 $v_{k+1}(s)$를 업데이트함
  $v_{k+1}(s) \doteq \max_a \mathbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) \mid S_t = s, A_t = a] \\ = \max_a \sum_{s', r} p(s', r \mid s, a) \left[ r + \gamma v_k(s') \right],$
  
  thresold보다 변화량이 작아질때까지 value function을 업데이트하다가, 이 value function으로 policy를 구함

summary

• 알고리즘은 state-value function $v_\pi (s)$ 혹은 $v_* (s)$에 의존함.
  각 iteration 당 시간복잡도는 $O(mn^2)$임(m: action, n : state)
  

• action-state value function에도 적용할 수 있음
  각 iteration 당 시간복잡도는 $O(m^2 n^2)$임
  
  policy iteration과 value iteration의 차이?

• policy itertaion
  - control 문제를 해결하기 위하여 (최적 정책을 찾기 위하여)

  • 특정 정책을 평가한 후, 그 정책을 개선하는 과정을 반복한다.
  • Bellman expectation equiation을 사용하여 현재 정책의 값을 평가하고, greedy policy improvement를 통해 정책을 개선하는 두 단계의 형태이다.

• value iteration
  - control 문제를 해결하기 위하여 (최적 정책을 찾기 위하여)

  • 정책을 평가하는 것이 아닌 글로벌한 value function 그 자체를 개선해 나간 후 policy를 정한다.
  • 즉 Bellman optimality equation을 사용하여 직접적으로 최적 가치를 찾는다. 최적 가치를 찾으면, 자연스럽게 바로 최적 정책을 찾을 수 있으므로 이 방식은 정책 평가와 개선이 하나의 단계로 통합되는 너낌이다.
  • 그러므로 하나의 반복문 안에서 optimal value를 찾고, 그에 따라 최적 정책을 수립하는 방식임. policy iteration보다 빠름