Model-free Prediction

Model-free Reinforcement Learning

MDP 모델이 알려져 있지 않는 상황에서 특정 정책에 따른 기대되는 return을 측정해보자!

• Model-free Prediction (evaluation)
  - 알려져있지 않은 MDP의 value function을 측정
  • 주어진 policy가 얼마나 좋은가?
• Model-free control (improvement)
  - 알려져있지 않은 MDP의 value function을 최적으로 만든다.
  • 어떻게 더 나은 policy를 학습시킬까?

What are Monte-Carlo Methods

• 주어진 문제를 해결하기 위해 랜덤 샘플링을 반복하여 수치적 근사치를 계산하는 방법
• 복잡하거나 불규칙한 문제에서도 유용하게 적용
  
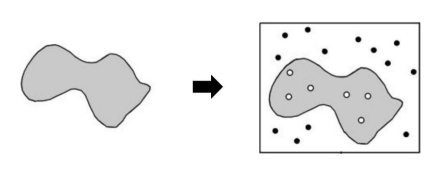
  위의 그림은 불규칙한 모양의 면적을 측정하는 예시임. 불규칙한 모양의 면적을 직접 측정하기는 어렵기 때문에, 이 모양이 포함된 범위 안에 무작위로 점을 찍어 샘플링함. 전체 점 중 모양 내부에 위치한 점의 비율을 계산하여 이 비율을 통해 전체 면적에 대한 불규칙한 모양의 면적을 추정함

Monte-Carlo Reinforcement Learning

• MC는 경험의 에피소드를 통해 직관적으로 학습함
• MC는 Model-free : MDP의 전이 확률/보상에 대한 지식 없이
• MC는 완전히 끝난 에피소드로부터 학습함 : no bootstrapping
• MC는 에피소드 전체의 평균 리턴 값을 통해 상태릐 가치를 학습함
  즉 특정 상태 s에 도달하는 여러 에피소드가 있을 때, 그 상태에서 시작하여 얻은 모든 리턴의 평균값을 구한다는 의미
• 오직 에피소딕한 MDP에 한해서만 가능(모든 에피소드가 끝나야함)

Monte-Carlo Policy Evaluation

• Goal : policy 하에서 경험적 에피소드로부터 $v_\pi(s)$를 학습한다.
  $S_1, A_1, R_2, \dots, S_k \sim \pi$
• return은 전체의 할인된 reward임. (실제 결과)
  $G_t = R_{t+1} + \gamma R_{t+2} + \gamma^{T-1} R_T$
• value function은 예상되는 return의 값임
  $V_{\pi}(s) = \mathbb{E}_{\pi} \left[ G_t \mid S_t = s \right]$
• 몬테카를로 정책 평가는 경험적인 mean return을 사용함. NOT expected return!!

First-Visit Monte-Carlo Policy Evaluation

• 특정 상태를 첫 번째로 방문했을 때의 return을 주구장창 계속 사용하는 몬테카를로 방법. 특정 상태를 중복 방문하더라도 첫 방문 시점의 return만을 반영하므로 first-visit이라는 이름이 붙음

• state s를 평가하기 위한 것으로
  - s가 첫번째로 방문된 time step t에 대해
  - 카운터 증가 : $N(s) \larr N(s_t )+1$
  - total return 증가 : $N(S_t) \leftarrow N(S_t) + 1$
  - value는 평균 return으로 계산 : $V(S_t) \leftarrow V(S_t) + \frac{1}{N(S_t)} (G_t - V(S_t))$
  - 무한번 반복하면 가치함수는 정책에 따른 것으로 수렴하게 됨
  
  첫 번째 에피소드에서 S2와 S3의 value를 구했다.
  두 번째 에피소드에서 S2의 value를 구할 때, 이전의 에피소드에서 구한 S2의 value를 사용했다.
  

Every-Visit Monte-Carlo Policy Evaluation

특정 상태를 방문할 때마다 리턴을 수집하여 평균을 구하는 방식임. first-visit과는 반대라고 볼 수 있음

• state s를 평가하기 위한 것으로
  - s가 방문된 매 time step t에 대해
  - 카운터 증가 :
  - total return 증가 :
  - value는 평균 return으로 계산 :
  - 무한번 반복하면 가치함수는 정책에 따른 것으로 수렴하게 됨 :
  
  S2의 경우 총 3번 발생하여 N의 값이 3이다. V의 경우, 평균을 구하기 위해 각 S2의 value를 N인 3으로 나누어 곱한다.
  S3은 한 번 발생하여 그냥 구햇당~

Incremental Mean

Temporal-Difference Learning

• TD는 에피소드를 완전히 끝낼 필요 없이, 에피소드를 진행하면서 학습을 한다.
• TD는 모델 프리임 : MDP의 모델을 알지못함
• TD는 끝나지 않은 에피소드로부터 학습함. (by bootstrapping)
• TD는 추측으로부터 추측을 업데이트함.

MC vs TD

• policy 하에서 경험한 에피소드로부터 가치함수 $v_\pi(s)$를 학습함.
• Incremental Monte-Carlo : MC 방식에서 상태 $S_t$는 다음과 같이 업데이트된다.
  $V(S_t) \leftarrow V(S_t) + \alpha \cdot (G_t - V(S_t))$
  여기서 G는 실제로 얻은 가치이고, V는 기존 가치이다. 오차에 학습률을 곱해 가치를 점진적으로 업데이트한다.
• Temproal-Difference :
  $V(S_t) \leftarrow V(S_t) + \alpha \left( R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \right)$
  - 예상되는 리턴값과 value의 차를 통해 업데이트한다.
  • $R_{t+1} + \gamma V(S_{t+1}$는 TD target
  • $\left( R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \right)$는 TD error이다.

Example: TD Policy Evaluation

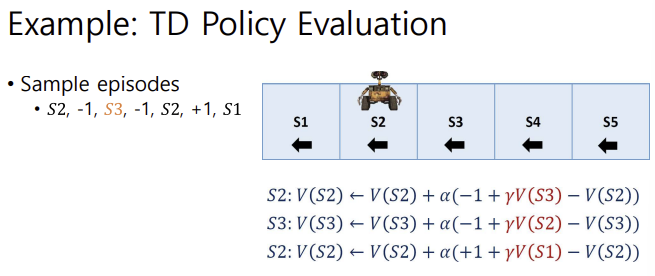
다음과 같이, 각 state의 value를 업데이트할 때에 (reward + 다음 state value - 현재 state value), 즉 TD error를 사용한다.

Bias / Variance Trade-Off

• bias는 잘못된 가정으로 인해 발생하는 오류의 정도를 뜻함
• variance는 오버피팅되어 input 데이터에 대해 민감하게 반응하는 정도를 뜻함. (훈련세트에 작은 변동이 발생하면 큰 에러가 발생하는 너낌)
  
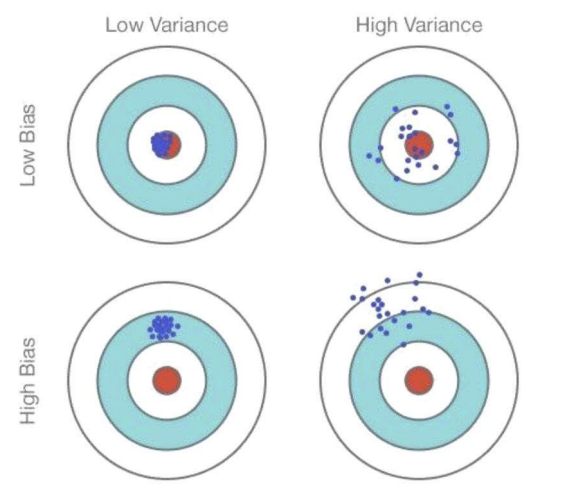
  bias가 높으면 걍 target이랑 멀고 낮으면 target이랑 가까움. variance가 낮으면 그림과 같이 데이터가 약간 변하더라도 예측이 크게 달라지지 않으며 안정적으로 중심에 모여있음. 반면 높으면 막 퍼짐
• 실제 reuturn 값인 G는 unbaised estimate of value function이다.
• 마찬가지로, true TD target은 unbiased임
• TD target인 $R_{t+1} + \gamma V(S_{t+1}$는 bias한 estimate이다.
• TD target은 실제 return보다 낮은 분산을 가진다. 왜냐하면 td target은 매 단계마다 예측에 기반한 비교적 안정적인 업데이트를 수행하기 때문에 에피소드 전체를 고려하는 리턴보다 값이 덜 변동함.

Bias / Variance of MC vs TD

• MC는 높은 variance, zero bias임.
  - MC는 에피소드 전체의 리턴을 통해 학습함. 에피소드마다 얻는 리턴이 다를 수 있기 때문에 추정치의 변동이 커서 분산이 높음
  • 각 에피소드가 끝난 후에 업데이트를 하기 때문에 결과가 예측 가능한 상황에서도 변동성이 크게 나타날 수 있음
  • 에피소드 전체를 통해 실제 리턴을 기반으로 업데이트하므로 장기적으로는 정확한 기대값에 수렴하게 됨.
  • Good Convergence Properties : MC는 수렴 특성이 좋음. 특히 함수 근사를 사용해도 잘 수렴함
  • 초기 값에 크게 민감하지 않으며 에피소드 단위로 학습하기 때문에 시간이 지나면 초기 값의 영향이 줄어듦
  • 직관적이며 사용하기 쉬움
• TD는 낮은 variance, some bias임
  - 매 스텝마다 다음 상태의 예측 값을 참고해 현재 상태의 가치를 업데이트함. 이 방식은 에피소드 전체를 기다릴 필요가 없고 중간에 조정이 이루어지기 때문에 변동성이 낮고 안정적임
  • 한 번의 에피소드를 학습하는 동안 여러 번의 업데이트가 진행되기 때문에 분산이 낮음
  • 다음 상태의 예측치를 참고해 학습하므로 초기 학습 단계에서 bias가 높을 수 있음
  • 따라서 MC랑 비교해서는 더 bias가 높게 나타남.

Batch MC and TD

• 유한한 데이터셋에 대한 배치 솔루션(데이터셋이 유한한 상태에서 주어진 데이터셋으로 학습 진행)
  - k개의 에피소드 셋들이 주어짐
  - k개의 에피소드에서 반복적으로 샘플을 고름
  - MC나 TD를 적용함
  이러한 방식으로 학습하면 MC는 정확한 기대 보상에 수렴하며, TD는 정책에 따른 현재 상태의 기대 가치에 수렴하게 됨.

MC vs TD

• 연산 효율성 비교
  - MC : 에피소드 종료 후 전체 리턴을 계산하여 업데이트를 수행하기 때문에 최종적으로 O(L)의 연산이 필요함. 에피소드가 길어지면 길어질수록 기다려야 하는 시간이 길어지므로 TD보다 업데이트 속도가 느림
  • TD : 매 스텝 업데이트를 하기 때문에 O(1)의 연산 복잡도를 가짐. 전체 에피소드 길이가 L이면 TD에서는 O(L)의 연산 복잡도로 에피소드 전체에 대한 업데이트가 가능함. 즉 각 단계마다 하나의 연산만 필요하기 때문에 계산효율이 좋음
• Markov property
  - MC : 마르코프 프로퍼티를 활용하지 않음. 에피소드 전체의 리턴을 사용하기 때문에 비마르코프 환경에서도 유용하게 작동함. 즉, 마르코프 프로퍼티가 없는 환경에서는 TD보다 MC가 더 효과적일 것. 예를 들어 과거의 정보가 현재 상태에 영향을 미칠 때에는 MC가 더 적합함.
  • TD : 마르코프 프로퍼티를 활용함. 즉 현재 상태만으로 다음 상태에 대한 정보를 예측하기 때문에 마르코프 프로퍼티가 있는 환경에서는 TD가 매우 효과적. 각 단계에서 바로 다음 상태의 전이를 기반으로 학습하기 때문에 효율적으로 학습 가능.

DP vs MC vs TD

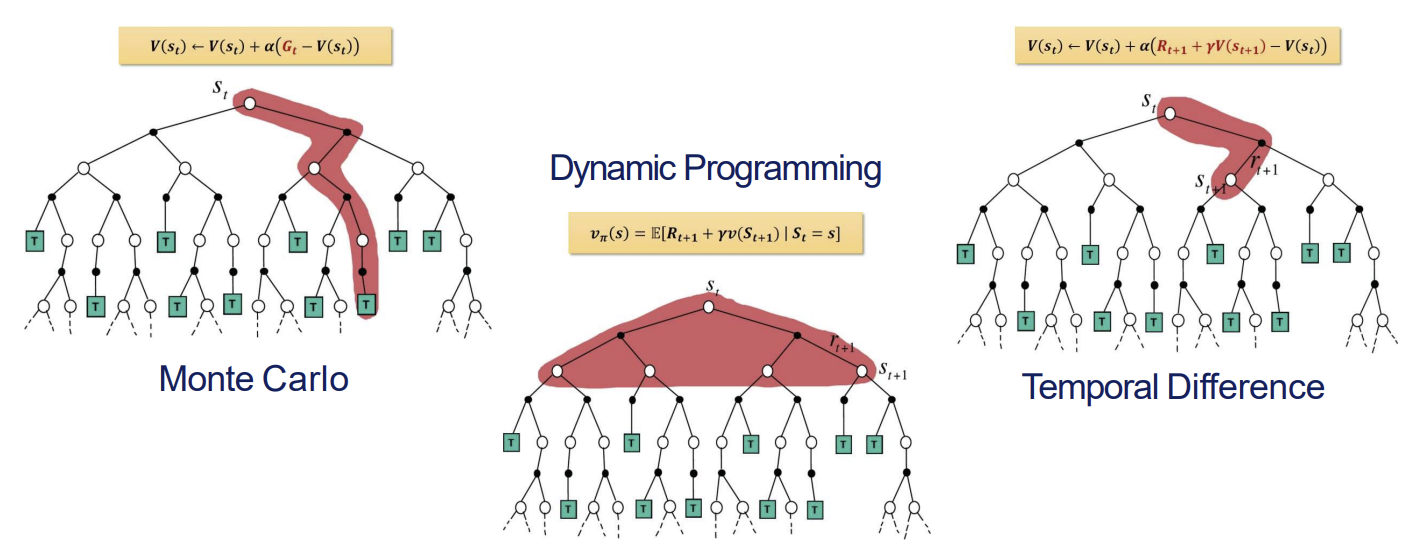
• MC
  - 에피소드가 종료 될때까지 기다렸다가 모든 리턴을 합산하여 평균으로 그 상태 가치를 업데이트함.
  • 에피소드 내의 현재상태에서 최종 상태까지의 모든 경로를 따라 누적 보상 G를 계산한 후 이를 사용하여 V 업데이트
• DP
  - MDP의 모델을 가지고 있어야 함.
  • 현재 상태 S에서 가능한 모든 다음 상태로의 전환을 고려하여 가치를 계산함. 따라서 빨간 영역이 모든 가능한 경로를 포함함
• TD
  - 에피소드 끝날 때까지 안 기다리고 각 스텝마다 업데이트를 함
  • 다음 상태의 예측치를 사용하여 업데이트함

Sampling and Bootstrapping

• sampling : 경험한 에피소드로부터 정보를 모으는 것
  - DP : sample 안함
  • MC : sample 함
  • TD : sample 함
• bootstrapping : 예측으로부터 업데이트를 함
  - DP : bootstrap 함
  • MC : bootstrap 안함
  • TD : bootstrap 함

n-step prediction

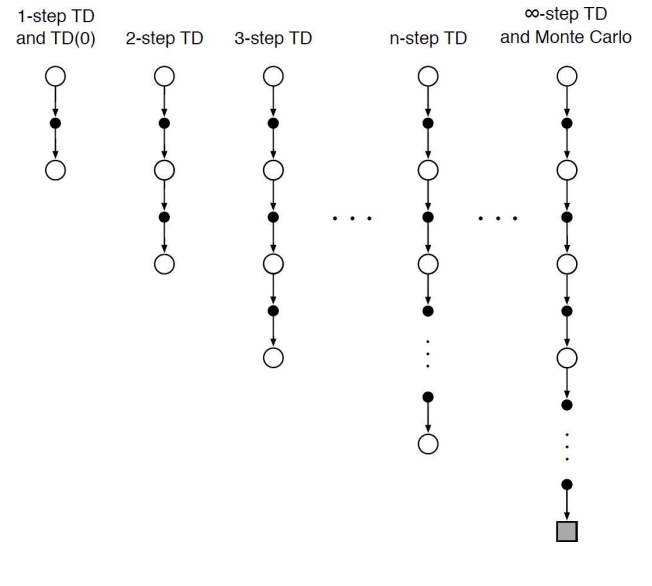
• 지금까지는 1-step TD/TD(0)에 대해 알아보았다. 1-step, 즉 바로 뒤의 미래뿐만 아니라 그 뒤의 뒤에까지, 더 나아가 MC처럼 끝까지 예측하는 TD는 어떨까? :
  $n = 1$
  $G_t^{(1)} = R_{t+1} + \gamma V(S_{t+1})$
  $n = 2$
  $G_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 V(S_{t+2})$
  $n = \infty \quad \text{(MC)}$
  $G_t^{(\infty)} = R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{T-1} R_T$
• n-step return을 정의하면 다음과 같다 :
  $G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n})$
• n-step td learning :
  $V(S_t) \leftarrow V(S_t) + \alpha \left( G_t^{(n)} - V(S_t) \right)$
  

Averaging n-Step returns

• 서로 다른 n-step learning의 평균을 낼 수 있음
  ex) 2-step과 4-step의 평균
  $\frac{1}{2} G^{(2)} + \frac{1}{2} G^{(4)}$
• 즉 서로 다른 time-step의 정보를 결합하는 것
• 효과적으로 모든 time-step의 정보들을 결합할 방법이 있을까?

$\lambda$-return

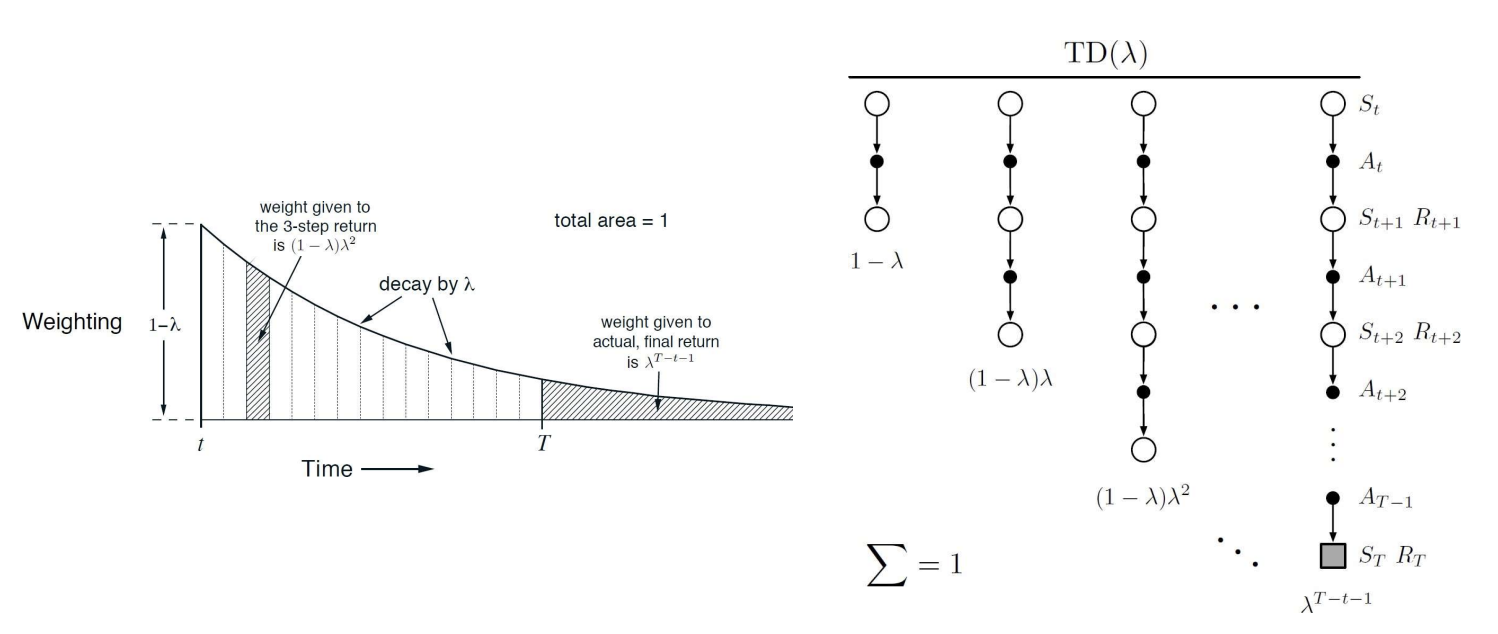
• n-step updates의 평균을 구하기 위한 방법으로써 TD($\lambda$)가 있다.
  - 여러 n-step 리턴을 가중 평균하여 상태 가치를 업데이트
  • 각 n-step 리턴은 $\lambda$에 의해 가중치가 부여됨
  • $\lambda$는 0과 1 사이의 값이며 n이 커질수록 $\lambda$의 제곱승으로 가중치가 점차 줄어듬. 즉 $\lambda$가 클수록 먼 미래의 리턴이 중요하게 반영됨
  • $\lambda$-return:
    $G_t^{\lambda} = (1 - \lambda) \sum_{n=1}^{\infty} \lambda^{n-1} G_{t:t+n}$
  • $\lambda$을 사용한 backup
    $V(s_t) = V(s_t) + \alpha \left[ G_t^{\lambda} - V(s_t) \right]$
• $\lambda$가 0이면 one-step TD임
• $\lambda$가 1이면 MC랑 똑같음!
  $G_t^{\lambda} = (1 - \lambda) \sum_{n=1}^{\infty} \lambda^{n-1} G_t^{(n)}$
  $= (1 - \lambda) \sum_{n=1}^{T - t - 1} \lambda^{n-1} G_t^{(n)} + \lambda^{T - t - 1} G_t$

Forward-View TD($\lambda$)

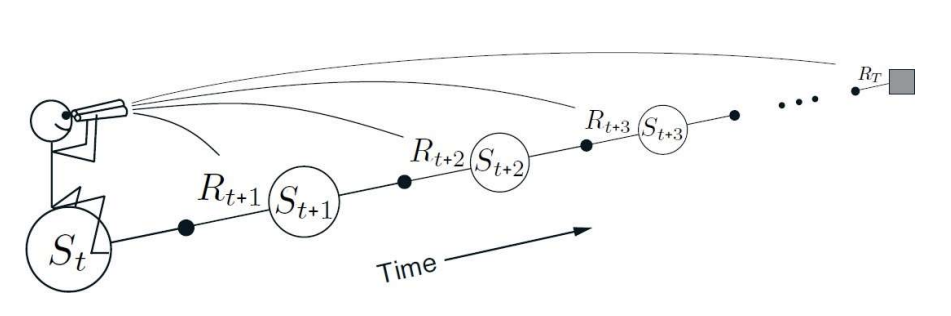
• 람다 리턴을 향해 가치 함수를 업데이트
  - Forward view TD($\lambda$)는 현재 상태의 가치를 람다 리턴 값으로 업데이트하는 방법임.
  • 람다 리턴은 다양한 스텝의 리턴을 가중 평균하여 계산된 값으로, 단기 및 장기 리턴을 모두 반영하여 상태 가치를 추정함
• forward-view
  - 현재 상태에서 미래로 이어지는 여러 스텝을 고려함
  • 그림과 같이 현재 상태에서 시작하여 이후의 상태들과 그에 따른 보상을 참고하여 람다 리턴을 계산함
  • 이를 통해 미래 누적 보상을 반영하여 현재 상태의 가치를 보다 정확하게 예측할 수 있음
• MC와의 유사성
  - Forward-view TD($\lambda$)는 람다 리턴을 계산하기 위해 에피소드가 종료될 때까지 모든 정보를 사용해야함. 즉, MC와 마찬가지로 완전한 에피소드가 필요
  • 따라서 단기 TD와 달리 한 에피소드가 끝나야만 계산이 가능하므로 실시간 업데이트가 어렵다는 한계가 있음