Model-free Control

Model-free control은 MDP를 모르는 상황에서, value function을 최적화 시키는 것!

Use of Model-Free Control

• MDP 모델링으로 많은 적용이 가능함
  - 장기, 헬리콥터 비행, 로봇 축구 등등...
• 이러한 문제들에 대해 적용가능
  - MDP 모델을 모름, but 경험이 sample될 수 있음
  • MDP 모델을 알지만 샘플링을 하지 않는 이상 계산상 직접적으로 하기 불가능한 상황

On and Off-Policy Learning

• On-policy learning
  - 직접적으로 경험
  • policy $\pi$를 따른 경험들로부터 $\pi$를 측정하고 평가함. 즉 경험한 policy와 평가하는 policy가 같음
• Off-policy learning
  - 다른 policy $\pi '$를 따른 경험으로부터 $\pi$를 측정하고 평가함. 즉 경험한 policy와 평가하는 policy가 서로 다름
  

Generalized Policy Iteration with MC Evaluation

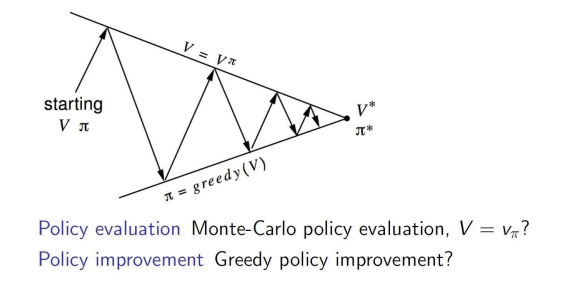
• 주어진 정책에 대해 가치 함수 V를 평가함. 이 과정에서는 MC 평가를 통해 정책의 각 상태에 대한 기대 보상을 추정.
• 계산된 가치 함수 V를 기반으로 더 나은 정책을 찾음. 이 과정에서 greedy 정책 개선을 통해 새로운 정책을 결정.

Model-Free Policy Improvement

• V(s)를 통한 greedy policy improvement는 MDP의 model을 알아야 함. 왜냐하면 특정 상태에서 가능한 모든 행동에 대해 보상함수와 전이 확률을 알고있어야 하기 때문임.
  $\pi'(s) = \arg\max_{a \in A} \mathcal{R}^a_s + \mathcal{P}_{ss'}^a V(s')$
• model free일 때에는 Q(s,a)를 통해 greedy policy improvement를 진행함. 모델 없이 Q(s,a)를 추정하고, 해당 값을 사용하여 각 상태에서 가장 큰 Q 값을 주는 행동을 선택
  $\pi'(s) = \arg\max_{a \in A} Q(s, a)$

Generalized Policy Iteration with Q-Function

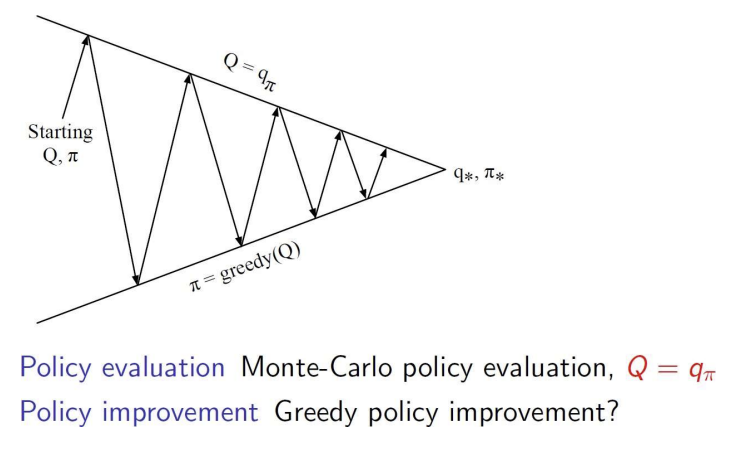
• 현재 정책에 대한 Q 함수를 평가함. 주어진 정책에 따라 각 상태와 행동 쌍의 기대 보상을 계산하는 과정임.
• 평가된 Q 함수를 기반으로 greedy 방법을 사용해 더 나은 정책을 찾음. 주어진 Q 값에서 최대의 기대 보상을 주는 행동을 선택하여 새로운 정책을 형성.
  

Exploration and Exploitation

• 강화학습은 시행착오를 통해 배움!
• 에이전트는 너무 많은 보상을 잃지 않는 선에서, 환경에서의 경험을 통해 좋음 정책을 찾아야함
• Exploration : 환경으로부터 더 많은 정보를 찾는 것! 최적의 행동만을 하는 것이 아닌, 다른 시도를 통해 더 나은 선택지가 있는가를 찾아봄. 맨날 가던 맛집이 아닌, 새로운 집을 try해보는 것을 의미~
• Exploitation : 최적의 행동을 선택함. 지금까지의 경험을 토대로 가장 value가 높았던 행동을 선택! 맨날 가던 맛집에 가는 것을 의미

$\epsilon$-Greedy Exploration

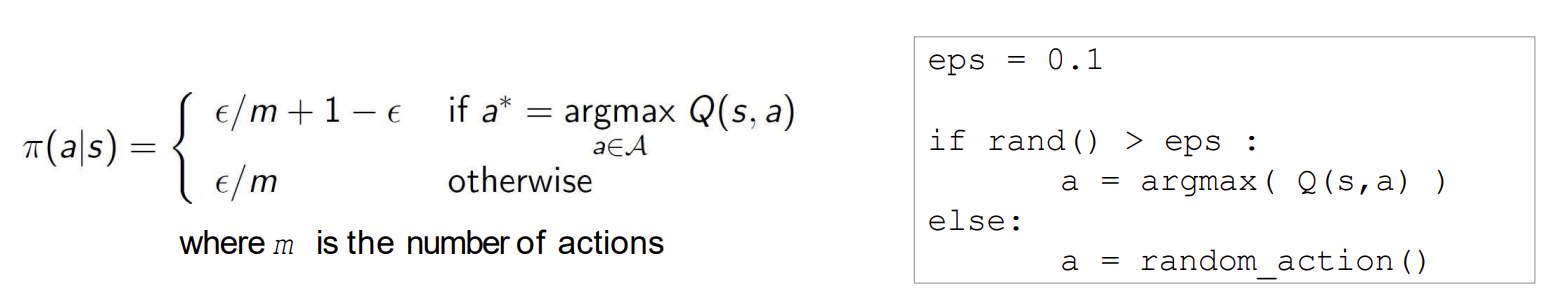
• 모든 행동을 일정 확률로 시도하도록 보장하는 간단한 방법임
• 모든 행동에 대한 탐색이 지속되도록 하기 위해 탐욕적 행동과 임의의 행동을 선택할 확률을 조정함
• 확률 $1-\epsilon$ : 현재 상태에서 가장 높은 Q 값을 가진 탐욕적 행동을 선택
• 확률 $\epsilon$ : 임의로 무작위 행동을 선택하여 탐색을 수행

• 어떤 $\epsilon$-Greedy에 대해서도, $\pi '$라는 새로운 $\epsilon$-Greedy 정책은 항상 기존 정책보다 더 나은 정책이라는 것을 보장한다.
• 첫 번째 줄 : 새로운 정책의 행동확률로, 각 q 값을 가중 평균한 값이다.
• 두 번째 줄 : $\epsilon$-Greedy에 따라, 확률 $\epsilon /m$으로 모든 행동을 시도하고, 확률 $1-\epsilon$으로 최적의 q값을 가진 행동을 선택한다
• 세 번째 줄 : greedy action을 선택하는 비율을 기반으로 policy improve 정리를 통해 더 나은 정책임을 보장함
• 최종적으로 새로운 정책이 기존 정책보다 더 나은 기대 보상을 가짐

일반 MC vs Variant MC

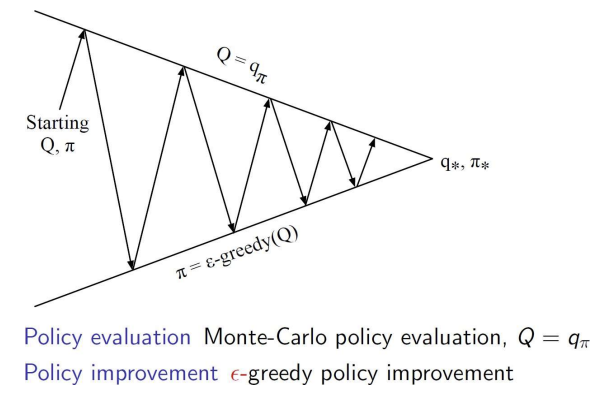
• 모델 없이 MC를 사용하여 정책 반복을 수행함
• 모든 에피소드를 수행한 후, 그 데이터를 가지고 정책 평가와 개선을 수행
  
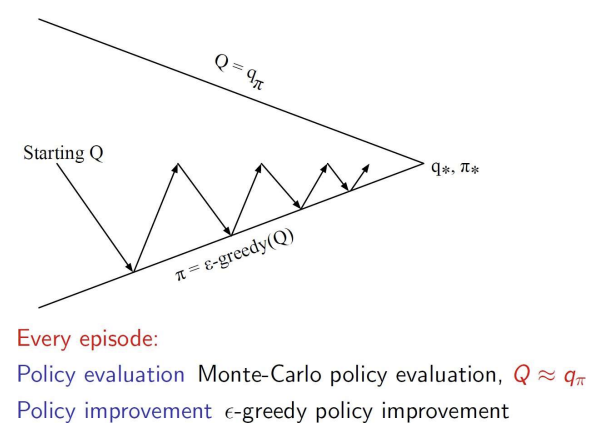
• 앞의 MC와 달리, 매 에피소드마다 정책 평가와 개선이 이루어짐
• 매 에피소드마다 MC 방법으로 정책 평가가 이루어짐, 즉 에피소드 단위로 Q 값이 업데이트됨.
• 그림에서 지그재그 쪽이 더 좁아진 패턴은 그만큼 정책 평가와 개선이 더욱 빈번하게 발생하는 것을 의미함!

Greedy in the Limit with Infinite Exploration (GLIE)

• 모든 state-action value 쌍이 무한히 탐색됨. N은 학습과정에서 s와 행동 a 쌍이 선택된 횟수를 뜻함. 이 조건은 모든 state-action 쌍이 무한히 탐색됨을 보장하여 학습 과정 중에 모든 가능한 행동을 충분히 시도할 수 있도록 함
• 정책이 탐욕적 정책에 수렴. 즉, 시간이 지나면서 정책이 점점 탐욕적 정책에 가까워지며 최종적으로 최적의 행동을 선택하게 됨. 이 조건은 학습이 진행됨에 따라 최적의 정책을 따르게 되는 것을 의미함
• example : $\epsilon$-Greedy를 사용하는 경우, 앱실론이 0으로 감소하도록 설정하여 GLIE 조건을 만족할 수 있음. 예를 들어 $1/k$로 설정하면 학습이 진행될수록 앱실론은 점점 작아지며 최적의 탐욕적 정책에 수렴하게 됨

Monte-Carlo Control

• 정책을 사용하여 에피소드를 샘플링함. (샘플링이라는 행위의 정확한 뜻이 헷갈렸었는데, 샘플링은 현재 정책을 기반으로 상태에서 행동을 선택하고 그 결과를 통해 얻은 상태-행동-보상 시퀀스를 기록하는 것이라고 함)
• 상태-행동 가치 함수를 업데이트한다. 이를 위해, 각 상태와 행동에 대해 N의 카운트를 하나 증가시킨다. %%1/N%%의 역할은 학습 속도를 조절하는 것으로, N이 증가할수록 업데이ㅡ 폭이 점점 작아지며 기존의 Q값이 점진적으로 안정화되도록 한다.
• 그리고 이렇게 업데이트된 새로운 액션-밸류 함수를 기반으로 policy를 개선한다.
  - 앱실론의 값을 적어지게 함
  • 앱실론-그리디 방식으로 정책을 업데이트함

MC vs Td Control

• TD 러닝은 MC에 비해 몇 가지 장점이 있음
  - Lower variance
  • Online : 한 스텝 끝나고 바로 업데이트 되는~
  • Incomplete Sequence : 전체 에피소드를 대상으로 하지 않기 때문에 안 끝난 시퀀스도 괜찮음
• 따라서 MC 대신 TD를 사용하는 것이 자연스럽...
  - $Q(S,A)$에 TD를 적용 : TD 방법으로 업데이트하여 더 효율적이고 빠른 정책 개선
  • 앱실론-그리드 정책 개선 : tD 학습으로 업데이트한 Q값을 기반으로 앱실론-그리드 방식으로 정책을 개선함
  • 매 스텝마다 업데이트!

Model-free Policy Iteration with Td Methods

• 정책 평가 스텝에 TD method를 사용
• 정책을 초기화함
• repeat :
  - 정책 평가 : 매 타임 스텝마다 td를 사용하여 $Q_\pi$를 계산함
  • 정책 개선 : MC와 마찬가지로, 앱실론 그리디 정책으로 개선함

Updating Action-Value Functions with SARSA

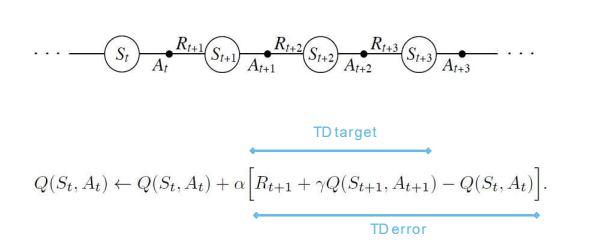
SARSA 알고리즘을 사용하여 행동 가치 함수 Q를 업데이트하는 과정을 설명함. SARSA는 TD 학습 방법 중 하나로, 다음 상태와 행동을 통해 현재 상태와 행동의 가치를 업데이트함.

• SARSA의 의미
  - SARSA는 각 타임스텝마다 다음과 같은 순서를 통해 학습함
  $S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1}$
  • 즉 현재 상태와 행동을 기반으로 다음 상태에서의 행동까지 고려하여 Q 값을 업데이트함
• 업데이트 식
  $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \right]$
  • $\alpha$ : 학습률로, 새로운 정보가 기존 정보에 얼마나 영향을 미칠지를 결정
  • $\gamma$ : 미래 보상이 현재 가치에 얼마나 영향을 미칠지를 결정
• TD target과 TD error
  - TD target : $R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})$
  • TD error : $\left[ R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \right]$
    • TD 에러가 클수록 기존의 Q 값에서 크게 벗어나기 때문에 Q 값을 크게 조정하여 새로운 정보를 반영
• SARSA의 작동 방식
  - 현재 정책에 따라 다음 행동을 선택하므로 exploration과 exploitation을 동시에 고려하여 학습.
  • 이 과정에서 각 타임스텝마다 Q 값이 업데이트되며 정책이 점차 최적 정책에 수렴하게 됨.

Policy Control with SARSA

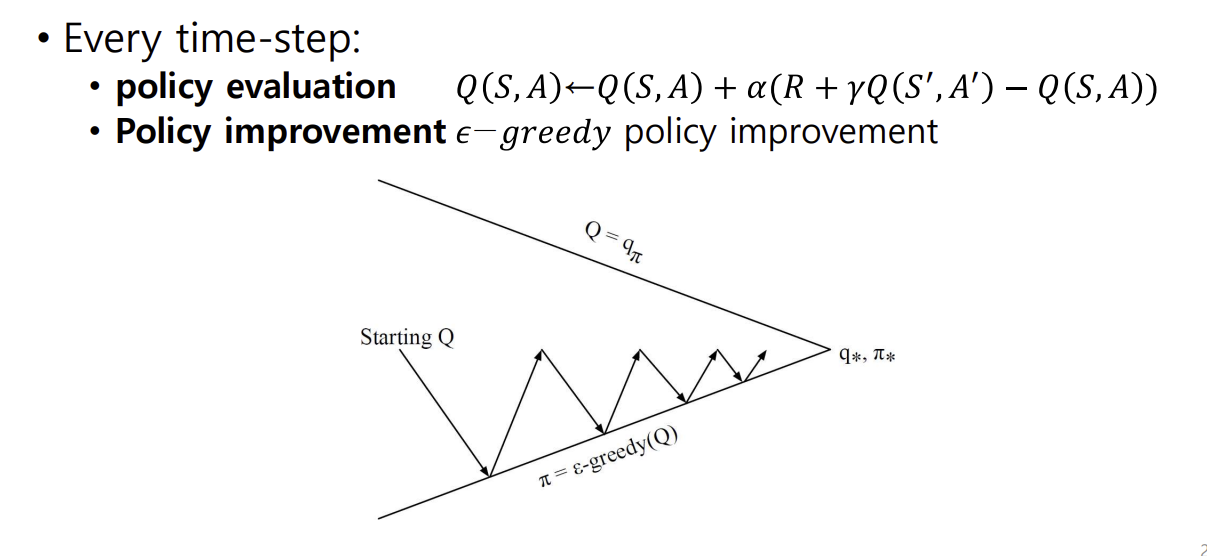
• 각 타임 스텝마다
  - policy evaluation : $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \right]$
  • policy improvement : 앱실론 그리디 policy improvement

SARSA algorithm

1. 알고리즘 파라미터 설정
- 학습률 $\alpha$ : 0과 1 사이의 값을 가지며 새롭게 들어오는 정보가 기존 정보에 얼마나 영향을 미칠지 결정
- $\epsilon$ : $\epsilon$-greedy 정책을 사용할 때, 일정 확률로 무작위 행동을 선택하여 탐색을 수행할 수 있도록 작은 양수로 설정함
2. 초기화
- 모든 action-value 쌍 Q(s,a)를 초기화. 종료 상태의 Q값은 0으로 설정.
3. 각 에피소드에 대해 반복
- 에피소드 시작 시 초기 상태 S를 설정
4. 에피소드의 각 단계에 대한 반복
- 현재 상태 s에서 정책에 따라 행동을 선택.
- 행동을 수행하여 보상과 다음 상태를 관찰
- 다음 상태에서 다음 행동을 선택. 이 역시 현재 정책에 따라 선택되며 SARSA는 on-policy 방식이므로 다음 상태에서의 다음 행동도 앱실론-그리디 정책을 따름.
5. Q 값 업데이트
- SARSA의 업데이트 식을 사용하여 Q를 업데이트함.
- SARSA는 현재 정책을 반영하여 Q 값을 업데이트하기 때문에 on-policy 방법으로 정책의 변화에 따라 안전하게 학습함.
6. 상태 및 행동 업데이트
현재 상태를 S'로, 현재 행동을 A'로 업데이트하여 에피소드의 다음 스텝으로 넘어감
7. 종료 조건
- 현재 상태가 종료 상태일 때까지 위의 과정이 반복됨. 종료 상태에 도달하면 해당 에피소드가 종료되고 다음 에피소드가 시작됨

n-Step SARSA

한 번에 하나의 타임스텝만 고려하는 대신 여러 타임스텝 동안의 return을 사용하여 업데이트를 수행

• n step 반환:
  $n = 1 \quad (\text{SARSA}) \text{일 때:}$
  $q^{(1)}_t = R_{t+1} + \gamma Q(S_{t+1})$
  $n = 2 \text{일 때:}$
  $q^{(2)}_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 Q(S_{t+2})$
  $\vdots$
  $n = \infty \quad (\text{MC}) \text{일 때:}$
  $q^{(\infty)}_t = R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{T-1} R_T$

  • n이 증가할수록 SARSA는 더 긴 미래의 보상을 반영하여 업데이트를 수행함

• n-step Q-return 정의
  - $q^{(n)}_t = R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{n-1} R_{t+n} + \gamma^n Q(S_{t+n})$

  • n 스텝 동안의 보상을 합산하고 마지막 스텝에서 Q를 추가하여 n-step 반환을 계산함
  • 미래의 n 타임스텝 동안의 보상을 반영하며 더 먼 미래까지 고려할수록 SARSA가 더 전체적인 시야를 가지고 학습하게 됨

• n step SARSA 업데이트:
  $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left( q^{(n)}_t - Q(S_t, A_t) \right)$
  - Q(s,a)를 n-step 반환 $q_{t}^{(n)}$ 방향으로 업데이트함

  • 여기서 $q_{t}^{(n)}$는 TD target으로 사용되며 현재의 Q(s,a)와의 차이를 줄여가며 학습이 이루어짐

Off-policy Learning

목표 정책과 행동 정책이 다른 경우 학습하는 방법임

• Off-policy learning 핵심 개념
  - 목표 정책 $\pi (a|s)$ : 학습하고자 하는 정책으로 최적화의 대상이 되는 정책임. 이 정책에 따라 상태-행동 가치 함수 $q_{\pi}(s,a)$ 또는 상태 가치 함수 $v_{\pi}$를 추정함.
  - 행동 정책 $\mu (a|s)$ : 실제로 에이전트가 따르는 정책임. 경험을 생성하기 위해 이 정책을 따르며 행동 정책은 목표 정책과 다를 수 있음
• Off-Policy Learning의 학습 과정
  - 에이전트는 행동 정책 $\mu$에 따라 경험을 생성한다. 즉, 에이전트는 행동 정책에 기반하여 상태 S에서 행동 A를 선택하고 보상 R을 받으며 새로운 상태 S'로 이동하는 일련의 시퀀스를 경험한다.
  • off-policy 학습을 통해 목표 정책의 가치 v나 q를 평가하고 목표 정책이 최적화하도록 학습한다.
• off-policy가 중요한 이유
  - 타 에이전트나 인간으로부터 학습 가능
  • 이전 정책으로 생성된 경험을 재사용 가능 : 과거에 사용했던 여러 정책으로부터 얻은 데이터를 활용하여 새로운 목표 정책을 학습할 수 있음. 데이터 효율성 up!
  • exploitation 정책을 사용하면서도 최적의 정책 학습 가능 : 탐험과 탐색을 동시에 수행하면서 목표로 하는 최적 정책을 학습할 수 있음. 예를 들어, 앱실론 그리디 정책과 같은 탐험적 정책을 따르면서도 실제로는 최적의 정책을 학습하는 방식임
  • 하나의 행동 정책으로 여러 목표 정책 동시에 학습 가능

Importance Sampling

어떤 분포에서 기대값을 추정하기 위해, 다른 분포에서 샘플을 뽑아 추정하는 기법

1. 기대값 계산의 목표:
   • 우리가 원하는 기대값은 $\mathbb{E}_{X \sim P}[f(X)]$, 즉 분포 P를 따르는 랜덤 변수 X에 대한 함수 f(X)의 기대값임.
   • 일반적으로 P 분포에서 직접 샘플링하여 기대값을 계산하지만, 샘플을 얻기 어려운 경우 다른 분포 Q에서 샘플링하여 계산할 수 있음.
2. 분포 Q를 사용한 기대값 계산
   • 원래 기대값 $\mathbb{E}_{X \sim P}[f(X)]$는 $P(X)f(X)$의 합으로 표현됨
   • 이때 분포 P 대신 다른 분포 Q를 사용하여 기대값을 계산하려면 분포 비율 $\frac{P(X)}{Q(X)}$을 보정해줘야 함
   • 즉 $P(X)f(X)$를 $Q(X)$로 나누고 다시 $Q(X)$를 곱해 위와 같이 변형함
3. 중요도 샘플링을 통한 기대값 표현
   • Q 분포를 기준으로 한 기대값으로 표현됨.
   • 이 식을 사용하면 분포 P에서 직접 샘플링하지 않고도 분포 Q에서 샘플을 뽑아 기대값을 추정할 수 있음.
   • $\frac{P(X)}{Q(X)}$은 중요도 가중치로, 분포 차이를 보정하기 위한 값

Importance Sampling for Off-Policy Monte-Carlo

Off-policy Mc 학습에서 중요도 샘플링을 사용하는 방법을 설명. 행동정책 $\mu$로 수집한 데이터를 통해 목표 정책 $\pi$의 기대값을 추정하는 것을 의미함
1. 행동 정책 $\mu$로 생성된 return을 사용하여 목표 정책 $\pi$를 평가
행동 정책과 목표 정책은 서로 다름. 이 경우, 중요도 샘플링을 사용하여 $\mu$에 따라 수집된 데이터로 $\pi$의 기대값을 추정함
2. 정책 유사성에 따라 return $G_t$에 가중치 부여
- G는 각 상태에서 얻은 보상과 다음 상태로의 전이 결과를 반영한 값.
- 중요도 샘플링은 행동정책과 목표 정책의 유사성에 따라 G에 가중치를 부여하여 정책의 차이를 보정함
3. 에피소드 전체에 걸쳐 중요도 샘플링 보정 적용
$G^{\pi / \mu}_t = \frac{\pi(A_t | S_t) \pi(A_{t+1} | S_{t+1}) \cdots \pi(A_T | S_T)}{\mu(A_t | S_t) \mu(A_{t+1} | S_{t+1}) \cdots \mu(A_T | S_T)} G_t$
- 목표 정책 하에서의 행동 확률을 행동 정책 하에서의 행동확률로 나누어 반환값 G를 정책의 차이에 따라 조정하는 역할을 함
4. 보정된 반환 G를 기준으로 가치함수 $V(S_{t})$ 업데이트
$V(S_t) \leftarrow V(S_t) + \alpha \left( G^{\pi / \mu}_t - V(S_t) \right)$
- 상태 가치 함수는 보정된 반환 방향으로 업데이트 된다.
- $\alpha$ : 학습률로, 새로운 정보가 기존 가치 함수에 얼마나 반영될지 결정
5. 제약사항
- 만약 행동 정책이 특정 상태-행동 쌍에 대해 확률이 0이라면 사용할 수 없음
- 중요도 샘플링을 사용하면 분산이 크게 증가할 수 있음

Importance Sampling for Off-Policy TD

TD 학습에서 중요도 샘플링을 사용하는 방법
1. 행동 정책으로 생성된 TD target $R_{t+1} + \gamma V(S_{t+1})$을 사용하여 목표 정책 평가
TD에서는 TD 목표를 통해 현재 상태 S의 가치를 업데이트함
2. 중요도 샘플링을 통해 TD 목표에 가중치 부여
Td 목표는 행동 정책에 따라 수집된 데이터이므로 이를 목표 정책 관점에서 평가하기 위해 중요도 샘플링 보정값 $\frac{\pi(S_t, A_t)}{\mu(S_t, A_t)}$을 적용함
보정값은 정책 비율로, 목표 정책과 행동 정책 간의 차이를 반영
3. 단일 중요도 샘플링 보정만 필요
앞선 MC와 달리 단일 스텝에서의 중요도 샘플링 보정만 필요함. 즉 S에서의 A에 대한 정책 비율만을 적용
4. MC 중요도 샘플링에 비해 훨씬 낮은 분산
MC는 전체 에피소드에 걸쳐서 중요도 샘플링 보정을 적용하기 때문에 분산이 크게 증가할 수 있음. 그러나 TD에서는 단일 타임스텝의 보정만 필요하므로 MC에 비해 분산이 낮고 학습이 더 안정적임.

Q-Learning: Off-policy TD Control

• 이제 action-values Q(s,a)에 대한 off-policy learning에 대해 생각해보자.

• 큐 러닝은 중요도 샘플링이 필요하지 않음. 이는 큐 러닝이 항상 다음 상태에서 최대 큐 값을 주는 행동을 목표로 업데이트하기 때문. 즉 행동 정책과 관계없이 최적 행동을 기준으로 학습하므로 행동 정책과 목표 정책 간의 보정을 위한 중요도 샘플링이 필요 없음

• 행동 정책을 사용하여 다음 행동 선택 : 다음 행동은 행동 정책에 따라 선택됨. 예를 들어 앱실론 그리디 정책을 사용하여 탐색을 수행할 수 있음

• Alternative action(대안적 행동) : 행동 정책에 따라 선택된 $A_{t+1}$과 상관없이 목표 정책에서는 다음 상태에서 최적 행동 $A'$를 가정하여 학습함. $A'$는 목표 정책에 따라 선택된 최적의 후속 행동으로, 다음 상태에서 최대 Q값을 주는 행동임.

• Q 값 업데이트 : 큐 러닝은 현재 상태와 행동 A에 대해 다음과 같은 식으로 Q 값을 업데이트함.
  $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left( R_{t+1} + \gamma Q(S_{t+1}, A') - Q(S_t, A_t) \right)$

• 행동 정책과 목표 정책의 분리 : 큐러닝은 off policy 방법이기 때문에 행동 정책과 목표 정책이 서로 다름. 행동 정책은 탐색을 포함하는 앱실론 그리디 정책을 사용할 수 있음. 목표 정책은 그리디 정책으로, 항상 현재 상태에서 가장 높은 큐 값을 가지는 최적 행동을 선택함. 즉 행동 정책과 목표 정책이 각자의 방식으로 개선을 하는거임.
  $\pi(S_t) = \arg\max_{a'} Q(S_t, a')$

• 큐러닝 업데이트 목표 : 큐러닝의 목표는 상태-행동 쌍 $(S_t, A_t)$에 대한 기대 보상을 최적화하는 것임. 큐러닝의 목표는 다음 상태에서 가장 높은 Q값을 가지는 행동을 기준으로 업데이트됨. 이를 통해 행동 정책은 탐색적인 특성을 가지는 동시에 최종적으로는 최적 목표 정책을 따르는 방향으로 수렴할 수 있음

• Q러닝 목표 단순화:
  $R_{t+1} + \gamma Q(S_{t+1}, A') = R_{t+1} + \gamma Q \left( S_{t+1}, \arg\max_{a'} Q(S_{t+1}, a') \right)$
  $= R_{t+1} + \max_{a'} \gamma Q(S_{t+1}, a')$

  • 첫번째 식에서 A'는 다음 상태에서 최대 Q값을 가지는 최적의 행동으로 선택됨
  • 따라서 A'는 argmax와 max로 단순화 시킬 수 있음

Q-Learning Algorithm

SARSA vs Q-Learning

SARSA 업데이트 식:

• 현재 정책에 따라 학습하는 on-policy 방법
• 다음 상태에서 현재 정책에 따라 선택된 행동의 Q값을 업데이트에 사용
• SARSA는 에이전트가 실제로 경험한 행동을 기준으로 학습하므로, 탐험이 주는 리스크를 포함한 학습이 이루어짐
  Q-learning 업데이트 식:
  $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma \max_{a} Q(S_{t+1}, a) - Q(S_t, A_t) \right]$
• 최적의 정책을 학습하는 off-policy 방법
• 다음 상태에서 가능한 행동 중 최적의 행동을 가정하고 해당 행동의 Q값을 업데이트에 사용함
• 큐러닝은 최적의 행동을 가정하여 학습하므로, 탐험을 하지 않고 최적의 정책으로 수렴할 가능성이 높음 !

Relationship between DP and TD

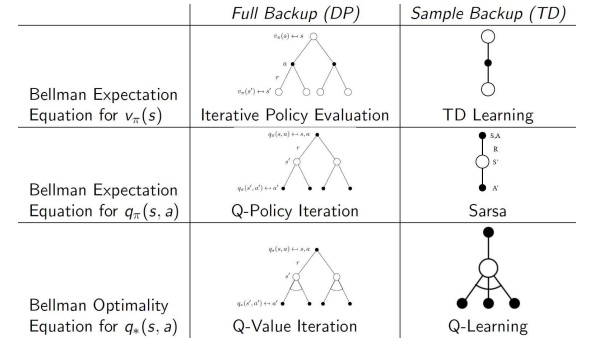
• DP : Full backup 방식으로, 모든 가능한 다음 상태에 대한 정보를 기반으로 가치 함수를 업데이트함. 즉, MDP의 모델을 전부 알고 있어야 하기 때문에 model-based 임

• TD : Sample backup 방식으로, 에이전트가 실제로 경험한 일부 샘플을 통해 가치 함수를 업데이트함. TD 방법은 경험으로 통해 학습하기 때문에 MDP의 전체 모델이 없어도 학습할 수 있어 model free에 해당

• 벨만 기대 방정식 for $v_{\pi}(s)$
  - DP : 상태 가치 함수를 계산하기 위해 모든 가능한 다음 상태에 대한 기대값을 계산하는 방식. 이를 통해 iterative policy evaluation 수행

  • TD : 에이전트가 경험한 샘플을 통해 상태 가치를 업데이트하는 방식으로 TD 학습이 이루어짐

• 벨만 기대 방정식 for $q_{\pi}(s,a)$
  - DP : 마찬가지로 모든 다음 상태와 그에 따른 보상에 대한 기대값을 기반으로 Q-policy iteration이 수행됨

  • TD : 경험을 통해 SARSA 알고리즘을 사용하여 q를 업데이트함. SARSA는 실제 경험에 기반하여 가치 함수를 업데이트하므로 on-policy임

• 벨만 최적성 방정식 :
  - DP : 모든 상태와 행동에 대해 최적의 기대 보상을 계산하여 q value iteration을 수행함. 최정 정책을 찾는데 사용
  - TD : 큐러닝을 통해 최적의 상태 행동 가치 q를 학습함. 큐러닝은 off-policy 방법으로, 다음 상태에서 가능한 행동 중 최적의 행동을 가정하여 업데이트함.
  
  자세한 수식은 이러함

Maximization Bias

• 제한된 샘플을 기반으로 가치 함수를 추정할 때, 편향된 최댓값이 발생하여 에이전트가 특정 행동에 대해 과대평가를 하는 문제를 의미함.

1. 0-mean 보상 환경 가정:
   • 단일상태 MDP에서 두 가지 행동 a1과 a2가 있으며, 이 행동들은 평균이 0인 랜덤 보상을 갖는다고 가정해보자.
   • 수학적으로는 $\mathbb{E}(r | a = a_1) = \mathbb{E}(r | a = a_2) = 0$ 이다.
   • 이 경우, 이론적으로는 $Q(s, a_1) = Q(s, a_2) = 0$ 이어야함. 즉, 어떤 행동을 선택해도 기대 보상은 0임.
2. 샘플 기반 추정:
   실제로는 에이전트가 a1이나 a2를 선택했을 때 관찰된 보상 샘플을 통해 유한한 샘플 추정치를 계산하게 됨. 이를 $\hat{Q}(s, a_1)$, $\hat{Q}(s, a_2)$ 로 나타냄. 하지만 이 값들은 샘플 수가 제한적이기 때문에 이론적 기대값인 0에서 벗어날 수 있음.
3. 탐욕적 정책의 편향
   • 에이전트는 추정된 값을 바탕으로 greedy 정책을 선택하게 됨.
   • greedy 정책 은 추정된 값이 가장 높은 행동을 선택하는 정책으로 정의됨.
     $\hat{a} = \arg \max_{a'} \hat{Q}(s, a')$
4. 최대화 편향의 발생
   • 두 행동의 진정한 기대값이 0임에도 불구하고 유한한 샘플로 인한 추정에서는 우연히 더 높은 추정값이 발생. 이 경우, 에이전트는 실제로는 기대 보상이 0인 행동을 긍정적으로 과대평가할 수 있음. 결과적으로, 두 추정치 중 최댓값은 0보다 클 가능성이 높음.

Double Learning

최대화 편향 문제를 해결하기 위한 Double Q learning을 소개함
1. 최대화 편향의 문제 :
- 최대화 편향은 유한 샘플로 학습할 때 Q 값의 추정치를 기준으로 탐욕적 정책을 선택하는 과정에서 발생함.
- 전체 모델을 아는 상태에서 구한 Q의 기대값과 유한 샘플로 학습한 Q 값의 추정치는 차이가 있을 수 있음. 이는 특정 행동을 실제보다 과대평가하게 만들고, 잘못된 학습 방향으로 이루어짐.
2. 더블 러닝의 원리 :
- 최대화 편향을 줄이기 위해 두 개의 독립적인 Q 값 추정치 Q1과 Q2를 사용함.
- 하나의 Q 값 추정치를 통해 최대 행동을 선택하고, 다른 Q 값 추정치를 통해 선택한 행동의 가치를 평가함으로써 편향을 줄임.
3. 두 개의 추정치 사용 방식
- 첫 번째 Q 추정치 Q1은 최대 행동 a을 선택하는 데에 사용됨. 즉, 얘는 유한한 샘플들의 결과로부터 argmax를 통해 최상 행동을 찾아냄
$$a^ = \arg\max_{a} Q_1(s, a) - 두 번째 Q 추정치 Q2는 a*에 대한 가치 평가를 수행하는 데 사용됨. 즉, 얘는 유한한 샘플들의 결과들을 통합하여 각 행동의 기대값(평균)을 구함 $$Q_2(s, a^*)
- 이 방식은 하나의 Q 값으로 최대 행동을 선택하고, 다른 Q 값으로 그 행동의 가치를 평가함으로써 최대화 편향을 완화할 수 있음.
- 이렇게 얻어진 두 Q값은 서로 교차 업데이트를 하며 편향된 Q 값을 안정화시킴. 교차 업데이트는 무작위로 Q1과 Q2 중 하나를 선택하여 수행됨. Q1이 선택되었을 때는 최적 행동을 선택하고, Q2로 그 행동의 가치를 평가함.
$Q_1(s, a) \leftarrow Q_1(s, a) + \alpha \left[ R + \gamma Q_2(s', a^*) - Q_1(s, a) \right]$
반대로 Q2가 선택된 경우에는 Q2로 평가함.
$Q_2(s, a) \leftarrow Q_2(s, a) + \alpha \left[ R + \gamma Q_1(s', a^*) - Q_2(s, a) \right]$
- 이렇게 하면 서로 독립적으로 학습하며 최대화 편향을 줄임!!!
4. 더블 큐러닝의 장점 :
- 두 개의 Q 값 추정치를 사용함으로써 최대화 편향이 줄어들어 학습의 안정성이 증가하고, 더 정확한 가치 추정이 가능해짐. 특히, 탐색과 최적화 간의 균형을 유지할 수 있어 에이전트가 잘못된 최적화를 수행하는 위험을 줄임.

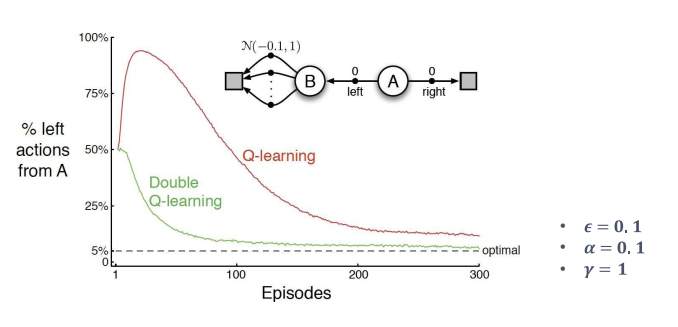
단순 큐러닝은 최대화 편향으로 인해 왼쪽 선택 비율이 높게 나타남. 상태 B의 노이즈 때문에 왼쪽 선택이 더 나은 선택이라고 잘못 학습. 시간이 지날수록 점차 편향이 줄긴 하는데, 여전히 편향이 남아있음
더블큐러닝은 두 Q 함수의 교차 업데이트를 통해 최대화 편향을 줄임. 이로 인해 왼쪽을 선택하는 비율이 빠르게 감소하고 옵티멀 정책에 더 근접하게 수렴

더블 큐러닝의 알고리즘은 다음과 같음. Q1과 Q2 각각이 선택될 때마다 저마다의 업데이트를 통해 교차 업데이트를 수행하여 과대 편향을 줄임!!!

껕!!!