Value function Approximation

Limitation of Q-Learning using a Q-Table

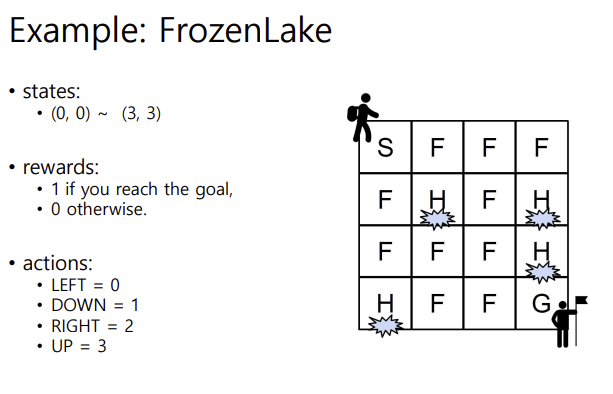
• small size map의 경우에는 Q 테이블을 정하는 것이 가능함. 예를 들어 이러한 프로즌레이크 문제에서는 Q 테이블이 4 곱하기 4 (그리드) * 4(행동) 으로, 64개의 저장공간이 필요함. 그런데 이것보다 더 커지면 어케됨???
  
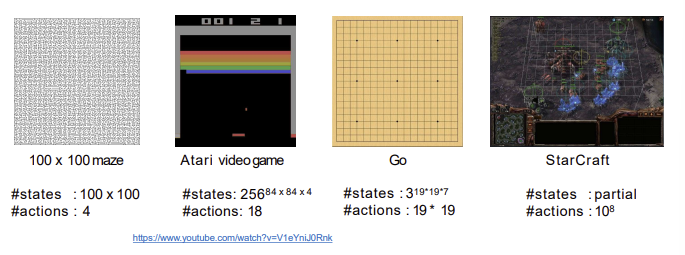
  이렇게 열라 큰 문제들을 맞닥뜨리면 걍 주옥되는 거임 ㅠ 이걸 다 어케 저장할건데 노답임 그냥. Q 테이블 저장하는 방식으로는 진짜 답이 없음. 무언가 대책이 필요함
  그럼 model free RL을 어떻게 확장해야할까?

Value Function Approximation

• 기존 가치 함수 표현 방식
  지금까지는 가치 함수 V(s)나 action 가치 함수 Q(s,a)를 lookup table로 표현함. lookup 테이블 방식에서는 각 상태 s에 대한 값 V(s) 또는 action 행동 쌍 Q(s,a)를 테이블 형태로 저장함.
• 큰 MDP에서의 문제점
  - 상태와 행동의 수가 많아지면 모든 state-action 쌍에 대한 값을 저장하기가 어려워짐.
  • 메모리가 과도하게 소모되며 각 상태에 대해 개별적으로 학습하는 것이 너무 느리거나 비현실적일 수 있음. 예를 들어 자율 주행 차량과 같은 대규모 상태 공간을 가진 MDP에서는 이러한 테이블 기반 접근법이 비효율적임.
• solution : vlaue function approximation
  - 이러한 문제를 해결하기 위해 가치 함수 근사를 사용함
  • 함수 근사에서는 테이블에 각 상태의 값을 저장하는 대신, 파라미터화된 함수(신경망이나 선형 모델 등)을 사용해 가치 함수를 근사함.
  • ex) 상태 가치 함수 근사 : $\hat{v}(s, \mathbf{w}) \approx v_{\pi}(s)$
  • ex) 상태-행동 가치 함수 근사 : $\hat{q}(s, a, \mathbf{w}) \approx q_{\pi}(s, a)$
  • 여기서 w는 함수 근사에 필요한 파라미터 벡터로 학습을 통해 최적의 값을 찾아가는 과정임.
• 가치 함수 근사의 장점 :
  - 메모리 절약 : 모든 상태나 상태-행동 쌍을 테이블에 저장하지 않고 파라미터화된 함수 하나만으로도 모든 상태에 대한 근사값을 계산할 수 있음.
  • 일반화 : 새로운 상태나 잘 알려져있지 않은 상태에 대해 빠르게 근사값을 계산할 수 있어 효율적임
  • 대규모 문제 해결 가능 : 특히 대규모의 상태 공간을 다루는 문제에 대해 테이블 기반 접근보다 훨씬 효과적임.

쉽게 설명하자면, Value Function Approximation는 상태 s나 상태-행동 쌍 (s,a)를 인풋으로 하고 아웃풋이 그에 대한 value인 함수임. 이러한 함수가 만들어지면, 각 상태에 대해 가장 높은 가치를 가지는 행동을 선택하여 최적 정책을 구할 수 있을 것!

Benefits of Approximation

• 상태나 상태-행동 쌍에 대해 컴팩트하게 일반화하여 표현
  - 메모리 절약
  • 계산 줄임
  • explore에 필요한 경험 감소

Feature-Based Representations

• 피쳐들의 벡터를 통해 state를 표현/묘사함
  - 여기서 말하는 피쳐란, state의 중요한 특징을 표현하는 real number임
  • 팩맨에서는 이런 피쳐들이 있을 수 있음 :
    • 가장 가까운 유령과의 거리
      • 가장 가까운 점과의 거리
      • 유령들의 수
      • 등등등..

Linear Value Functions

• 피쳐들의 선형적 결합으로 value function을 표현한 거임.
  $\hat{v}(S, \mathbf{w}) = x(S)^{\top} \mathbf{w} = \sum_{j=1}^{n} x_j(S) w_j$
  • 특성벡터와 가중치벡터의 내적으로 예측을 진행함. 각 피쳐가 가중치랑 곱해지는 것임! 그리고 그걸 더함
• $\hat{v}$과 $v$ 간의 mean-squared error를 최소화하는 벡터 w를 찾아야함.
  $J(\mathbf{w}) = \mathbb{E}_{\pi} \left[ \left( v_{\pi}(S) - \hat{v}(S, \mathbf{w}) \right)^2 \right]$
  여기서 기대값 E가 오차를 감싸는 이유는, 특정 상태에서만 오차를 최소화하는 것이 아니라 모든 상태에 걸쳐 평균적인 오차를 최소화하고자 하기 때문임.
• 로컬 미니멈을 찾는 그래디언트 디센트
  $\Delta \mathbf{w} = -\frac{1}{2} \alpha \nabla_{\mathbf{w}} J(\mathbf{w})$
  $= \alpha \mathbb{E}_{\pi} \left[ (v_{\pi}(S) - \hat{v}(S, \mathbf{w})) \nabla_{\mathbf{w}} \hat{v}(S, \mathbf{w}) \right]$
  - 오차함수를 최소화하기 위해 사용. 파라미터 w를 조정하여 오차 함수를 최소화하는 것이 목표임
  • 기울기 $\nabla_{\mathbf{w}} J(\mathbf{w})$는 오차 함수 J(w)에 대한 w의 변화율을 의미함. 기울기는 오차가 가장 빨리 증가하는 방향을 나타내므로, 기울기의 반대 방향으로 이동하여 오차를 줄여나감
  • 그래서 가중치 업데이트는 이렇게 이루어짐 : $-\frac{1}{2} \alpha \nabla_{\mathbf{w}} J(\mathbf{w})$
    여기서 알파는 학습률로 업데이트되는 속도를 조절함. 이 값을 통해 오차 함수의 기울기 방향으로 조금씩 이동하면서 최적의 파라미터를 찾아냄
  • 위의 기울기 표현을 풀어서 쓰면 그 아래의 식임. 해당 식은 오차와 근사된 가치함수의 기울기를 곱한 값의 기대값을 통해 파라미터를 업데이트함을 나타냄.

Gradient Descent

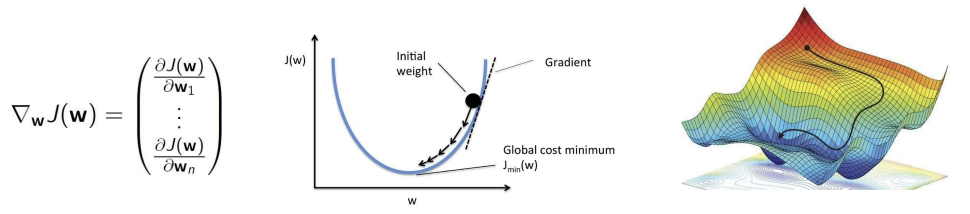
• J(w)는 파라미터 벡터 w에 대한 미분 가능한 함수로, 이 함수의 값을 최소화하는 w를 찾아내는 것이 목표임. 이 함수는 오차 함수일 수도 있고, 모델 성능을 평가하는 지표일 수도 있음.
• 목적은 J(w)를 최소화하는 파라미터 w를 찾는것. 이를 위해 기울기를 계산하여, 기울기의 반대 방향으로 이동함. 경사하강법은 이러한 과정을 반복하면서 점진적으로 최적값에 수렴함.
• 기울기 $\nabla_{\mathbf{w}} J(\mathbf{w})$ :
  - 기울기는 함수 J(w)가 w의 각 구성요소에 대해 얼마나 빠르게 증가하거나 감소하는지를 나타내는 변화율 벡터임. 기울기의 정의는 다음과 같음 :
  $\nabla_{\mathbf{w}} J(\mathbf{w}) = \begin{pmatrix} \frac{\partial J(\mathbf{w})}{\partial w_1} \\ \vdots \\ \frac{\partial J(\mathbf{w})}{\partial w_n} \end{pmatrix}$
  • 이 벡터는 각 파라미터 w_i에 대해 미분값을 가지며, 기울기의 방향이 곧 함수가 가장 빠르게 증가하는 방향이 됨.
• 경사하강법 과정:
  - 초기 파라미터에서 시작하여 기울기의 반대 방향으로 파라미터를 업데이트 해나감.
  • 초기 weight에서 출발하여 gradient 방향으로 이동하고 최종적으로 글로벌 cost minimum 지점에 도달하게 됨
  • 이렇게 기울기의 반대 방향으로 이동함으로써 오차를 최소화하는 최적의 파라미터 값을 찾을 수 있음.

Incremental Prediction Algorithms

• 실제 가치 함수 $v_{\pi}(s)$와 타겟 값:
  - 이상적으로는 true 가치 함수 $v_{\pi}(s)$를 사용하여 학습하고 싶지만, 강화학습에서는 슈퍼바이저(감독자)가 없고, 오직 보상만 주어짐

  • 따라서 실제 가치 함수 대신, 타겟 값을 설정함.
  • MC와 TD는 각각 다른 타겟 값을 사용함

• MC 방법:
  - MC에서는 에피소드가 끝난 후 누적 보상 G를 사용하여 상태의 가치를 추정함

  • 가중치 업데이트는 다음과 같이 이루어짐:
    $\Delta \mathbf{w} = \alpha \left( G_t - \hat{v}(S_t, \mathbf{w}) \right) \nabla_{\mathbf{w}} \hat{v}(S_t, \mathbf{w})$

    • G : 상태 s에서 시작하여 에피소드가 끝날 때까지 얻은 누적 보상
      • 차이점(G-v_hat) : 실제 누적 보상과 예측된 가치의 차이
      • 이 차이를 이용해 w를 조정하여 다음 번 가치 예측이 더 정확해지도록 함

• TD 방법:
  - TD에서는 에피소드가 끝날 때까지 기다리지 않고 매 단계마다 TD 타겟을 사용하여 상태의 가치를 추정함.

  • 가중치 업데이트는 다음과 같이 이루어짐:
    $\Delta \mathbf{w} = \alpha \left( R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}) - \hat{v}(S_t, \mathbf{w}) \right) \nabla_{\mathbf{w}} \hat{v}(S_t, \mathbf{w})$
    • TD target : 현재 보상과 다음 상태의 가치를 할인율 감마로 조합하여 계산
    • TD 차이 : 현재 가치 추정과 TD 타겟의 차이로, 이 값을 이용해 가중치를 업데이트함.

• MC와 TD의 차이
  - MC
  - 전체 에피소드가 종료된 후 누적 보상 G를 사용하여 가중치를 업데이트함.
  - 에피소드가 길 경우, 시간이 너무 소요함

  • TD
    • 에피소드 중간에도 매 스텝마다 즉각적인 보상과 다음 상태의 가치를 사용하여 가중치를 업데이트함.
      • 더 빠르게 업데이트 가능하며 에피소드 중간에도 중간에 학습이 가능함

Control with Value Function Approximation

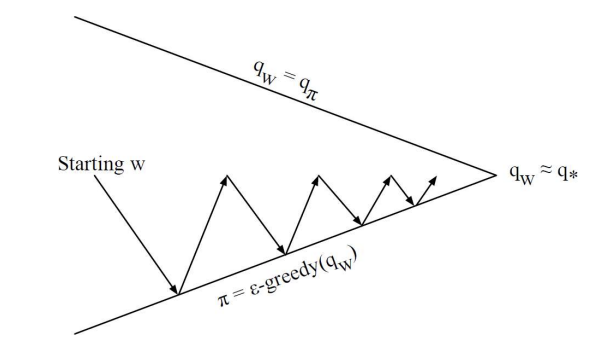
가치 함수 근사를 이용한 제어에 대해 설명하고 있음. 여기서 목표는 정책 평가와 정책 개선을 반복하며 정책에 수렴하는 것임

• 정책 평가
  - 주어진 정책에 대해 상태 행동 가치 함수 $q_{\pi}(s,a)$를 근사하여, 현재 정책의 성능을 평가함.
  • 가치 함수 근사를 사용하여 $q_{\pi}(s,a)$를 직접적으로 추정하지 않고(action을 저장하는 방식 X) 파라미터화된 함수 ^${q_{\pi}(s,a)}$를 통해 근사함. 이를 위해 파라미터 w를 업데이트함.
• 정책 개선
  - 정책 평가 후, 현 정책에서 더 나은 행동을 선택하는 새로운 정책을 만듦
  • 여기서 앱실론 그리디 정책을 사용하여 exploration과 exploitation 사이의 균형을 유지하며 정책을 개선함. 이 과정을 통해 점진적으로 더 나은 정책을 찾으며 최적의 정책에 수렴함.
• 과정의 반복:
  - 시작점에서 정책 평가와 정책 개선을 반복하면서 최적의 정책에 가까워지는 과정을 나타냄. 그림에서 볼 수 있듯, 시작점에서 시작해 반복적인 평가와 개선을 통해 최적의 상태-행동 가치 함수에 수렴하게 됨
  

Linear Action-Value Function Approximation

• 상태와 행동을 특성 벡터로 표현
  - 상태 S와 행동 A의 조합을 특성 벡터 x(S,A)로 나타냄.
  • 이 특성 벡터는 상태와 행동을 설명하는 여러 특성 값들로 이루어져있으며 다음과 같은 형태를 지님 :
    $x(S, A) = \begin{pmatrix} x_1(S, A) \\ \vdots \\ x_n(S, A) \end{pmatrix}$
  • 각 특성 x(S,A)는 상태와 행동의 특정한 특성을 나타내며, 학습을 통해 가치 함수에 영향을 미치는 요소로 작용함
• 행동-가치 함수의 선형 결합 표현
  - 상태와 행동의 특성 벡터 x(S,A)와 가중치 벡터 w의 내적을 통해 행동-가치 함수 ^q(S,A,w)를 근사함.
  • 이 선형 결합을 수식으로 나타내면 다음과 같음 :
    $\hat{q}(S, A, \mathbf{w}) = x(S, A)^{\top} \mathbf{w} = \sum_{j=1}^{n} x_j(S, A) w_j$
  • 내적 : 상태와 행동에 대한 가치의 추정값을 생성
  • w : 각 특성에 대한 가중치로 학습을 통해 최적화됨

Action-Value Function Approximation

• 행동-가치 함수 근사:
  - 목표는 상태 S와 행동 A에 대해 근사된 행동-가치 함수 ^q(S,A,w)를 학습하여 실제 정책의 행동 가치함수 $$q_{\pi}(S,A)에 가까워지도록 하는 것임.
  • 이를 달성하기 위해 가중치 벡터 w를 조정함
• 오차 함수 J(w)
  - 이 오차 함수는 평균 제곱 오차(MSE)로 근사된 행동-가치 함수 ^q(S,A,w)와 실제 행동-가치 함수 $q_{\pi}(S,A)$의 차이를 최소화하는 방식으로 정의됨
  • 오차 함수는 다음과 같음 :
    $J(\mathbf{w}) = \mathbb{E}_{\pi} \left[ \left( q_{\pi}(S, A) - \hat{q}(S, A, \mathbf{w}) \right)^2 \right]$
  • 이 함수는 실제 값과 예측 값 간의 차이를 제곱하여 평균화한 값으로 오차를 최소화하는 방향으로 학습이 이루어지도록 함
• 확률적 경사 하강법(SGD):
  $-\frac{1}{2} \nabla_{\mathbf{w}} J(\mathbf{w}) = \left( q_{\pi}(S, A) - \hat{q}(S, A, \mathbf{w}) \right) \nabla_{\mathbf{w}} \hat{q}(S, A, \mathbf{w})$
  $\Delta \mathbf{w} = \alpha \left( q_{\pi}(S, A) - \hat{q}(S, A, \mathbf{w}) \right) \nabla_{\mathbf{w}} \hat{q}(S, A, \mathbf{w})$
  - 오차 함수를 최소화하기 위해 기울기를 계산하여 가중치 w를 업데이트함
  • SGD의 업데이트 과정은 다음과 같음:
  • 학습률 : 얼마나 크게 가중치를 업데이트할지 결정
  • 오차 : 예측된 값과 실제 값 간의 차이로 오차가 클수록 가중치가 크게 조정됨
  • 기울기 : 예측된 행동-가치 함수의 파라미터에 대한 변화율로, 오차를 최소화하는 방향으로 이동하게됨

Incremental Control Algorithms

MC, SARSA, Q-learning 세 가지 방법에서 목표 값을 정의하고 이를 통해 가중치 w를 업데이트하는 방식을 설명

• 기본 아이디어:
  - 예측과 마찬가지로 제어에서도 실제 행동가치 함수 대신 사용할 목표값 target이 필요함.
  • 각 알고리즘은 서로 다른 방식의 목표값을 사용하여 가중치 업데이트를 수행함
• MC
  - MC에서는 에피소드 종료 후 얻은 누적 보상 G를 목표값으로 사용함.
  • 가중치 업데이트는 다음과 같음:
    $\Delta \mathbf{w} = \alpha (G_t - \hat{Q}(s_t, a_t; \mathbf{w})) \nabla_{\mathbf{w}} \hat{Q}(s_t, a_t; \mathbf{w})$
  • 여기서 G는 에피소드가 끝날 때까지 누적된 보상으로, 에피소드 단위로 업데이트가 이루어짐
• SARSA
  - SARSA는 TD 타겟을 사용하여 가중치를 업데이트함
  • 이 방법은 현재 근사된 가치와 다음 상태의 실제 보상 R을 사용하여 매 단계마다 업데이트가 이루어짐
  • 가중치 업데이트는 다음과 같음:
    $\Delta \mathbf{w} = \alpha (R + \gamma \hat{Q}(s', a'; \mathbf{w}) - \hat{Q}(s, a; \mathbf{w})) \nabla_{\mathbf{w}} \hat{Q}(s, a; \mathbf{w})$
  • 여기서 SARSA는 실제 다음 행동 a'에 따라 학습하는 on-policy 방법임
• Q-learning
  - 큐러닝은 TD 타겟을 사용하여 가중치를 업데이트함
  • 현재 보상 R과 다음상태에서의 최대 행동 가치 값을 목표로 삼아, 매 단계마다 업데이트를 수행함.
  • 가중치 업데이트는 다음과 같음:
    $\Delta \mathbf{w} = \alpha \left( R + \gamma \max_{a'} \hat{Q}(s', a'; \mathbf{w}) - \hat{Q}(s, a; \mathbf{w}) \right) \nabla_{\mathbf{w}} \hat{Q}(s, a; \mathbf{w})$
  • off policy 방법으로, 목표 정책은 탐욕적으로 학습하되 행동 정책은 다를 수 있음

Type of Value Function Approximation

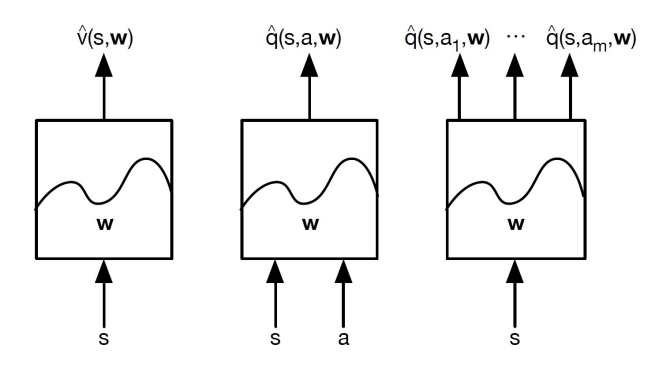
가치 함수 근사 유형을 설명하는 사진임. 각 블록은 상태 가치 함수와 행동 가치 함수를 파라미터 w로 표현하는 방식을 보여줌. 여기서 각 유형은 상태와 행동을 입력으로 받아, 특정 가치를 예측하는 함수로 구성됨.
1. 상태 가치 함수 근사 ^v(s,w)
- 입력 s는 상태만 포함되며 출력은 해당 상태의 가치 ^v(s,w)임
- 주어진 상태에 대해 단일 가치를 예측함
2. 상태-행동 가치 함수 근사 ^q(s,a,w)
- 입력 s와 a는 각각 상태와 행동이며 출력은 특정 상태에서 특정 행동을 선택할 때의 가치 ^q(s,a,w)이다.
- 이 함수는 상태와 행동의 쌍에 대해 해당 조합의 가치를 예상하여 정책을 학습하는 데 유용함
3. 다중 행동 가치 함수 근사 ^q(s,a1,w), ^q(s,a2,w), ..., ^q(s,am,w)
- 입력은 상태 s이며 출력은 각 행동에 대한 가치 함수 ^q(s,ai,w)임
- 특정 상태에서 모든 가능한 행동에 대해 각각의 가치를 계산하여 가장 좋은 행동을 선택하는 데 유리함.