flash attention

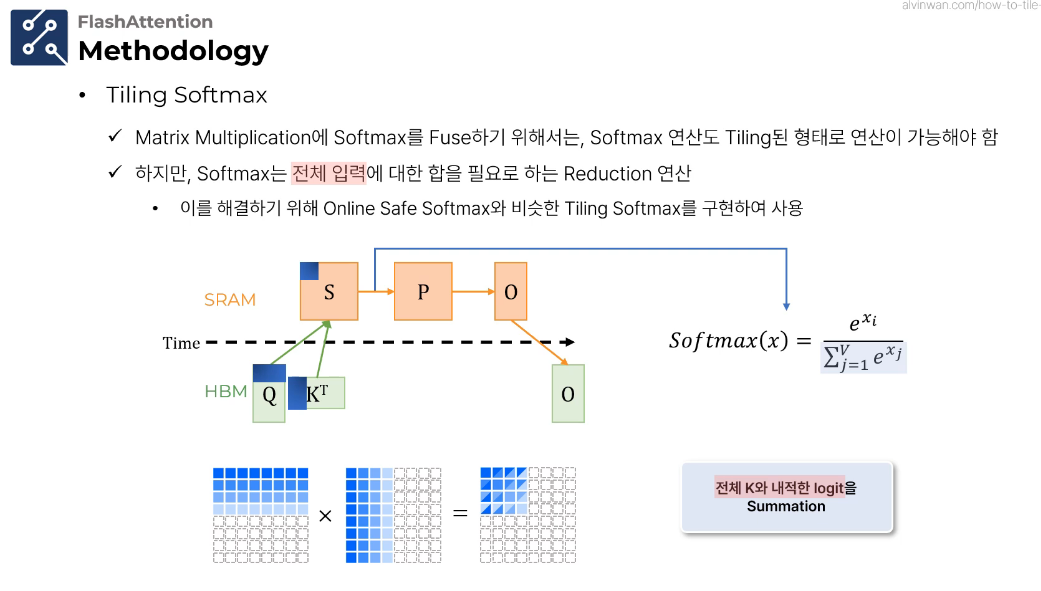
1. 실제 값 예시를 통한 설명:
   입력값: [24, 12, 18]

일반 Softmax (Algorithm 1) 계산과정:

1) e^24 = 2.648912×10^10
2) e^12 = 162754.8
3) e^18 = 65659969.1

d = e^24 + e^12 + e^18 = 2.648912×10^10

y1 = e^24/d = 0.9999
y2 = e^12/d = 0.0000
y3 = e^18/d = 0.0001

Online Safe Softmax (Algorithm 3) 계산과정:

1) 최대값 m = 24 찾기

2) 정규화된 지수값 계산:
   e^(24-24) = 1
   e^(12-24) = e^(-12) = 6.14×10^-6
   e^(18-24) = e^(-6) = 0.00247

3) 정규화된 합계 계산:
   d = 1 + 6.14×10^-6 + 0.00247 = 1.00247

4) 최종 결과:
   y1 = 1/1.00247 = 0.9975
   y2 = 6.14×10^-6/1.00247 = 0.000006
   y3 = 0.00247/1.00247 = 0.00246

2. Overflow 문제 상세 설명:
   a) 컴퓨터의 수 표현 한계:

• 일반적인 32비트 float는 약 ±3.4×10^38 범위의 수를 표현
• 64비트 double은 약 ±1.8×10^308 범위의 수를 표현

b) Overflow 발생 예시:

입력값이 [1000, 999, 998]일 경우:
e^1000 ≈ 1.97×10^434 (double 범위 초과)
e^999 ≈ 7.24×10^433 (double 범위 초과)
e^998 ≈ 2.66×10^433 (double 범위 초과)

c) 문제점:

• 범위를 초과하는 계산 시 Infinity 값 반환
• 분모가 Infinity가 되어 정확한 확률 계산 불가
• 작은 값들은 완전히 무시되어 0으로 처리됨

d) Safe Softmax가 이를 해결하는 방법:

최대값(1000)을 빼고 계산:
e^(1000-1000) = 1
e^(999-1000) = e^(-1) = 0.368
e^(998-1000) = e^(-2) = 0.135

이제 계산 가능한 범위 내의 숫자로 정확한 확률 계산 가능

---

Online Safe Softmax의 순차적 처리 과정을 실제 데이터 [5, 2, 8, 3]를 사용해 단계별로 설명

1. 첫 번째 요소 (j=1, x₁=5) 처리:

m₁ = max(m₀, x₁) = max(-∞, 5) = 5
d₁ = d₀ × e^(m₀ - m₁) + e^(x₁ - m₁)
   = 0 × e^(-∞ - 5) + e^(5 - 5)
   = 0 + 1
   = 1

2. 두 번째 요소 (j=2, x₂=2) 처리:

m₂ = max(m₁, x₂) = max(5, 2) = 5
d₂ = d₁ × e^(m₁ - m₂) + e^(x₂ - m₂)
   = 1 × e^(5 - 5) + e^(2 - 5)
   = 1 × 1 + e^(-3)
   = 1 + 0.0498
   = 1.0498

3. 세 번째 요소 (j=3, x₃=8) 처리:

m₃ = max(m₂, x₃) = max(5, 8) = 8
d₃ = d₂ × e^(m₂ - m₃) + e^(x₃ - m₃)
   = 1.0498 × e^(5 - 8) + e^(8 - 8)
   = 1.0498 × e^(-3) + 1
   = 1.0498 × 0.0498 + 1
   = 0.0522 + 1
   = 1.0522

4. 네 번째 요소 (j=4, x₄=3) 처리:

m₄ = max(m₃, x₄) = max(8, 3) = 8
d₄ = d₃ × e^(m₃ - m₄) + e^(x₄ - m₄)
   = 1.0522 × e^(8 - 8) + e^(3 - 8)
   = 1.0522 × 1 + e^(-5)
   = 1.0522 + 0.0067
   = 1.0589

5. 최종 Softmax 값 계산 (y_i = e^(x_i - m_v) / d_v):

y₁ = e^(5 - 8) / 1.0589 = e^(-3) / 1.0589 = 0.0498 / 1.0589 = 0.0470
y₂ = e^(2 - 8) / 1.0589 = e^(-6) / 1.0589 = 0.0025 / 1.0589 = 0.0024
y₃ = e^(8 - 8) / 1.0589 = e^(0) / 1.0589 = 1 / 1.0589 = 0.9444
y₃ = e^(3 - 8) / 1.0589 = e^(-5) / 1.0589 = 0.0067 / 1.0589 = 0.0063

주요 특징 설명:
1. 순차처리의 이점:

• 메모리 효율적: 전체 시퀀스를 저장할 필요 없음
• 실시간 처리 가능: 새로운 입력이 들어올 때마다 바로 처리

2. 수치 안정성:

   • 최대값(m_j)을 기준으로 정규화하여 overflow 방지
   • 모든 지수 계산이 음수 또는 0을 지수로 사용

3. 계산 효율성:

   • 이전 계산 결과(d_j-1)를 재활용
   • 각 단계에서 필요한 계산량이 일정함

이런 방식으로 Online Safe Softmax는 수치적 안정성을 유지하면서도 효율적인 순차 처리가 가능합니다.

---

Online Safe Softmax와 Safe Softmax의 동등성 증명

1. 구체적인 수치 예제로 단계별 비교:
   입력값: [5, 2, 8, 3]

Safe Softmax 계산:

1) 최대값 찾기: m = 8

2) 정규화된 지수값:
   x₁=5: exp(5-8) = exp(-3) = 0.0498
   x₂=2: exp(2-8) = exp(-6) = 0.0025
   x₃=8: exp(8-8) = exp(0) = 1.0000
   x₄=3: exp(3-8) = exp(-5) = 0.0067

3) 분모 계산:
   sum = 0.0498 + 0.0025 + 1.0000 + 0.0067 = 1.059

4) 최종 확률:
   y₁ = 0.0498/1.059 = 0.0470
   y₂ = 0.0025/1.059 = 0.0024
   y₃ = 1.0000/1.059 = 0.9444
   y₄ = 0.0067/1.059 = 0.0063

Online Safe Softmax 순차 계산:

1) x₁=5 처리:
   m₁ = 5
   d₁ = exp(5-5) = 1

2) x₂=2 처리:
   m₂ = max(5,2) = 5
   d₂ = 1×exp(5-5) + exp(2-5)
   d₂ = 1 + 0.0498 = 1.0498

3) x₃=8 처리:
   m₃ = max(5,8) = 8
   d₃ = 1.0498×exp(5-8) + exp(8-8)
   d₃ = 1.0498×0.0498 + 1
   d₃ = 0.0522 + 1 = 1.0522

4) x₄=3 처리:
   m₄ = max(8,3) = 8
   d₄ = 1.0522×exp(8-8) + exp(3-8)
   d₄ = 1.0522×1 + 0.0067
   d₄ = 1.0589

2. 수학적 동등성 증명:

Online Safe Softmax의 d_j 계산을 펼쳐보면:

d₁ = exp(x₁-m₁)

d₂ = d₁×exp(m₁-m₂) + exp(x₂-m₂)
   = exp(x₁-m₁)×exp(m₁-m₂) + exp(x₂-m₂)
   = exp(x₁-m₂) + exp(x₂-m₂)

d₃ = d₂×exp(m₂-m₃) + exp(x₃-m₃)
   = [exp(x₁-m₂) + exp(x₂-m₂)]×exp(m₂-m₃) + exp(x₃-m₃)
   = exp(x₁-m₃) + exp(x₂-m₃) + exp(x₃-m₃)

d₄ = d₃×exp(m₃-m₄) + exp(x₄-m₄)
   = [exp(x₁-m₃) + exp(x₂-m₃) + exp(x₃-m₃)]×exp(m₃-m₄) + exp(x₄-m₄)
   = exp(x₁-m₄) + exp(x₂-m₄) + exp(x₃-m₄) + exp(x₄-m₄)

3. 최종 결과 비교:

Online Safe Softmax의 최종 형태:
y_i = exp(x_i - m_final) / d_final

이는 Safe Softmax의 형태와 동일:
y_i = exp(x_i - m) / Σexp(x_j - m)

4. 주요 차이점:

• Safe Softmax: 모든 데이터를 한번에 처리
• Online Safe Softmax: 순차적 처리, 메모리 효율적

5. 장점:

• 수치적 안정성 유지
• 메모리 효율성
• 실시간 처리 가능
• 동일한 결과 보장

이처럼 Online Safe Softmax는 Safe Softmax의 수학적 변형이며, 계산 과정만 다를 뿐 최종적으로 동일한 결과를 산출합니다. 이는 수치적 안정성을 유지하면서도 효율적인 순차 처리를 가능하게 합니다.

https://www.youtube.com/watch?v=ktpbVgQKy0g