Generative Model은 무엇인가?

• Explicit model: 입력이 주어졌을때, 그것에 대한 확률값 $p(x)$을 얻을 수 있는 모델
  단순히 generate만 할 수 있는 모델은 implicit model이라 부름

그러면 $p(x)$는 어떻게 표현할 수 있을까?

---

Basic Discrete Distributions

• 베르누이 분포: class가 2개뿐이라 binary
• 카테고리 분포: class가 m개

예제) $p(x)$는 어떻게 구할까?

• State가 n개일 경우 나머지 모든 확률을 안다면 마지막 1개의 확률은 1-나머지이기 때문에 필요한 parameter의 수는 n-1개

• input이 커질수록 필요한 parameter의 수가 너무 많아지는 문제가 발생
  이를 해결하기 위해 independence라는 개념을 도입
• 모든 픽셀이 independent하다고 가정하면, n개의 parameter로 $2^n$개의 상태를 표현 가능(모든 픽셀이 0 또는 1이기 때문)

---

Conditional Independence

• 하지만 언제나 모든 input이 independent할 수는 없기 때문에 몇가지 제약을 둠
• Chain rule, Bayes' rule은 언제나 exact하지만 Conditional Independence는 가정
• Conditional Independence: z가 주어졌을때, x,y가 항상 independent하다면, x의 probability distribution을 표현하는데 z가 주어지면 y는 없어도 된다

• $p(x_1, ..., x_n)$: joint distribution
• chain rule은 fully dependent할 때랑 parameter 수가 달라지는게 없다

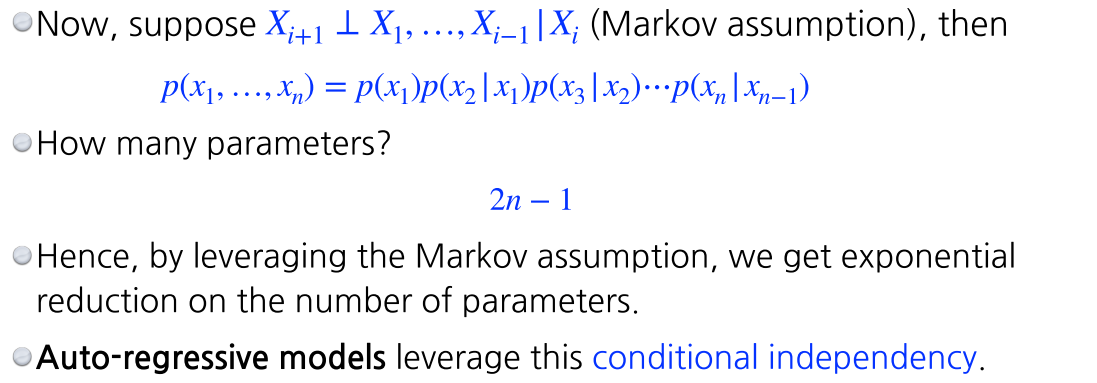
• Markov assumption: $X_i$번째 pixel은 $X_{i-1}$에만 dependent하고 나머지 $X_{1\sim i}$에는 independent
• Markov assumption을 통해 parameter 수를 줄일 수 있다

---

Auto-regressive Model

• Auto-regressive model: 어떤 정보가 이전 정보에 dependent한 model을 의미
  i번째 pixel이 i-1에만 dependent해도 auto-regressive, 1~i-1에 모두 dependent해도 auto-regressive
• auto-regressive model을 활용하기 위해서는 ordering(순서)가 중요함
  순서를 메기는 것에 따라 성능이 달라지기도 한다
• 어떤식으로 conditional independency를 주느냐에 따라 전체 model structure가 달라진다

---

NADE: Neural Autoregressive Density Estimator

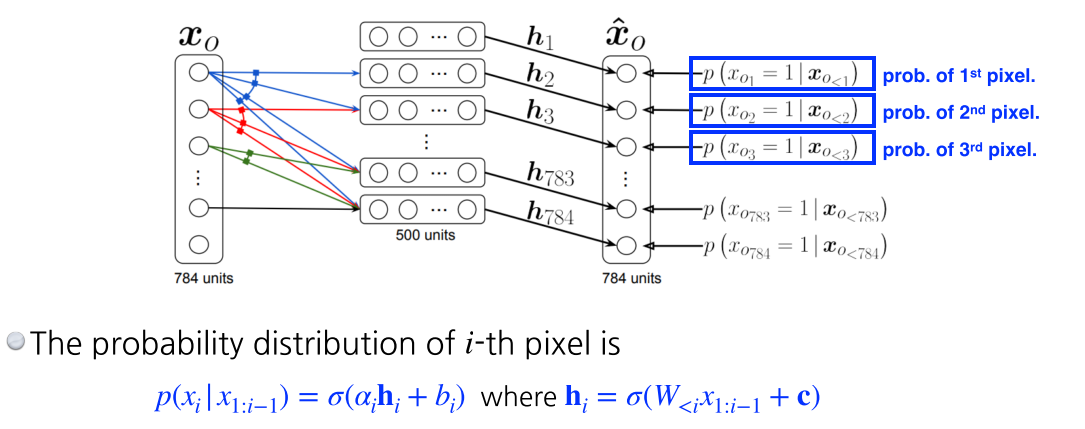
• i번째 pixel은 i-1개의 pixel에 dependent한 모델
  --> autoregressive
• 입력차원이 계속 달라지기 때문에 weight가 계속 커진다

• 임의의 input에 대한 확률을 구할 수 있기 때문에 explicit model
• explicit model은 일반적으로 Density Estimator라는 얘기가 들어가있다
  Density = probability Density기 때문에

---

Pixel RNN

• i번째 pixel의 R을 먼저 만들고, G, B를 순차적으로 만듬
• ordering을 어떻게 하느냐에 따라 2가지로 나뉨

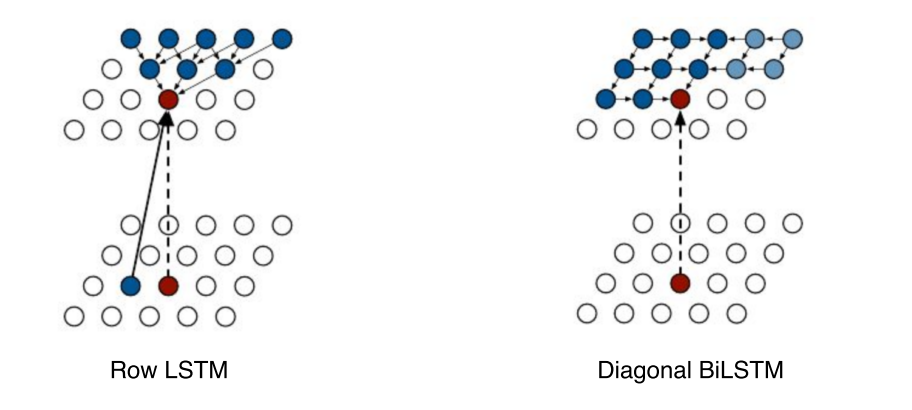
• Row: 자기 위쪽 정보를 활용
• Diagonal: 자기 이전 정보들을 활용