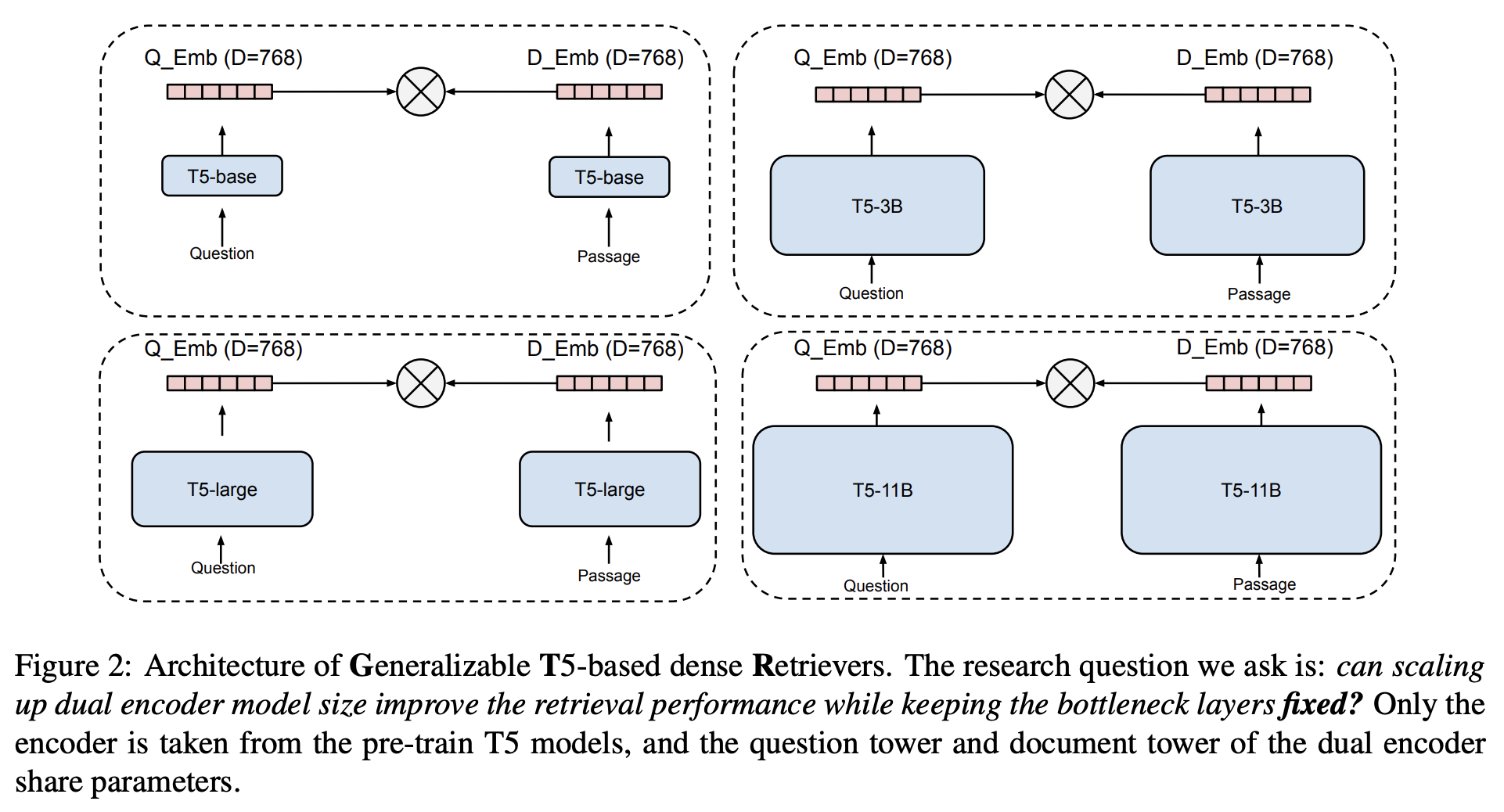
IR 모델들 중 듀얼인코더를 사용할 때 데이터 도메인 변경 시 점수가 많이 떨어지게 되는데, 그 이유로 bottleneck 레이어(query, passage의 dot product 하는 부분)의 한계를 들기도 한다.

이전 연구 (Lu et al., 2021; Khattab and Zaharia, 2020)에서 간단하게 consine similarity를 이용해서 query, document 연관성을 보는 것이 충분하지 않을 수 있다는 의견이 있었고, BEIR 데이터셋을 소개한 논문에서는 듀얼 인코더가 OOD 문제가 있으며 일반화 성능이 좋아지기 위해서는 query, document 사이의 interaction이 중요하다고 주장했다.

이 연구에서는

• 정말 bottleneck 레이어 때문에 domain shift 어려운 것인지
• bottleneck 레이어 단의 어떤 영향력 없이(interaction limited) domain shift를 잘해낼 수 있는지를

확인하고자 모델 사이즈를 늘리고 bottleneck 사이즈를 동일하게 맞추어서 실험을 진행하였다.

결과로 bottleneck 부분의 영향도를 최소화하면서도 모델을 크게했을 때 out of domain 결과가 좋아지는 것을 확인했다.

Multi-stage training

이 논문에서는 아래와 같이 multi-stage training을 진행했는데,
여기에서 말하는 multi-stage에는 1) Pre-training stage, 2) Fine-tuning stage를 말한다.

Pre-training stage

• 가장 먼저 기존 훈련된 T5 encoder를 이용해 모델을 초기화한다.

• 이 연구에서 말하는 Pre-training stage에서는 web-mined corpus(question-answer pairs, conversations)를 이용해 훈련을 진행했다. (Contrastive learning)

• Sentence-T5에서 제시한 구조처럼 mean pooling으로 구성된 듀얼인코더 구조를 사용해서 pre-training을 진행한다.

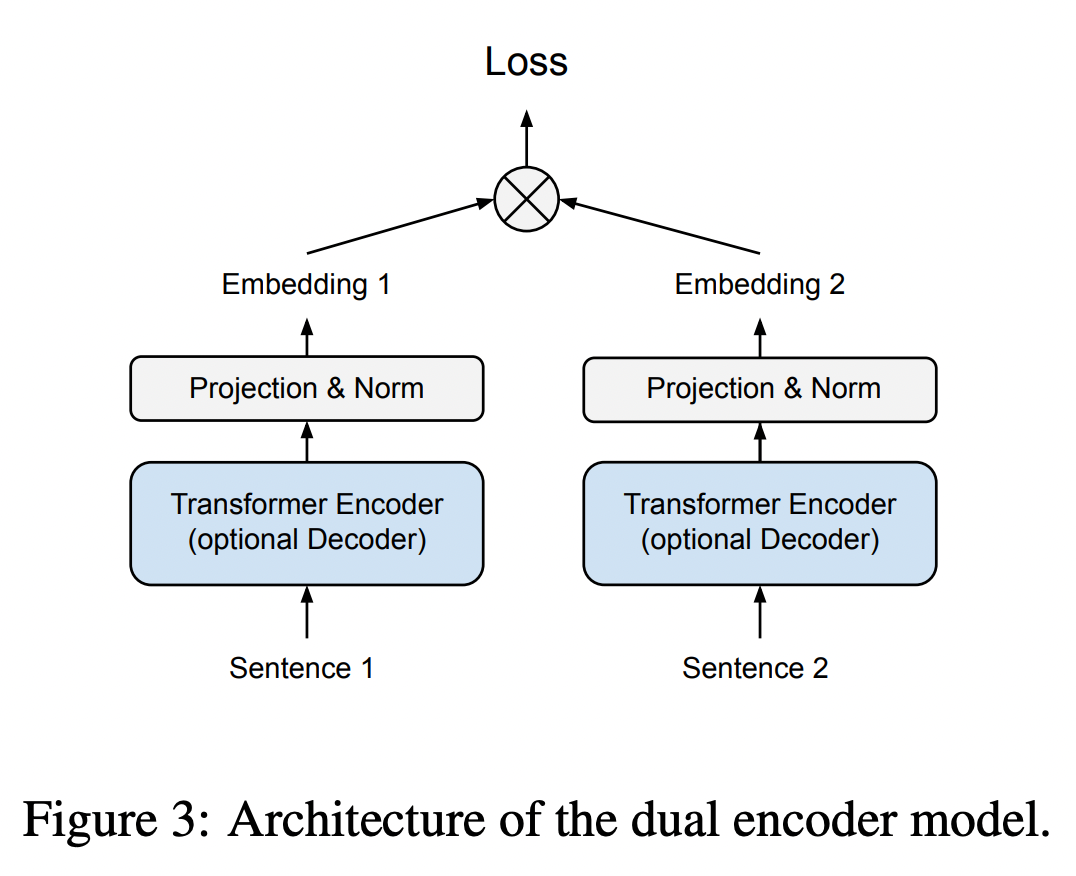
  • 여기에서 말하는 mean pooling은 전체 결과 토큰들의 평균을 말한다.

• Loss function
  

• Community QA 데이터를 사용했으며 이 데이터는 Reddit, Stack-Overflow와 같은 QA 웹사이트들을 말한다.

  • 2 billion question-answer pairs

Fine-tuning stage

• 이 연구에서는 MSMARCO, NQ 데이터(a high quality search corpus)를 이용해서 파인튜닝을 진행했다.
• Loss function
  

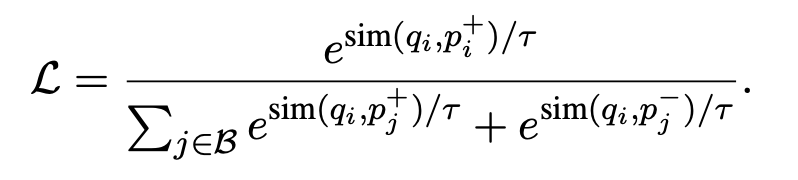
Experiments

• JAX를 이용했으며 Cloud TPU-V8로 학습을 진행했다.
• Base, Large, XL, XXL 사이즈의 아키텍처를 훈련시켰다.
  
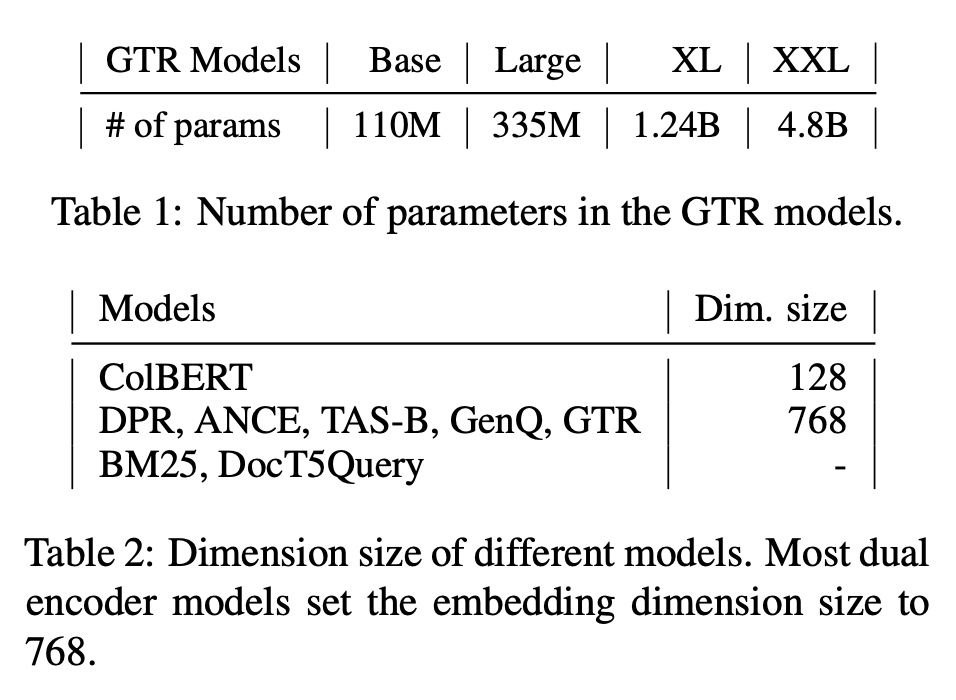
• T5 모델과 동일한 vocab 사용
• Batch size 2048, Temperature 0.01, initial LR 1e-3
• 800K Pre-training, 20K Fine-tuning 진행
• Fine-tuning 단계에서는 RocketQA 에서 공개한 hard negative 이용했다. (MSMARCO)
• BEIR 데이터셋에 대해서는 query 64, document 512 tokens
• 평균 토큰 수에 따라,
  • (Trec-News, Robust-04) document length 768 (가능한가?)
  • (ArguAna) question length 512

• In-domain performance
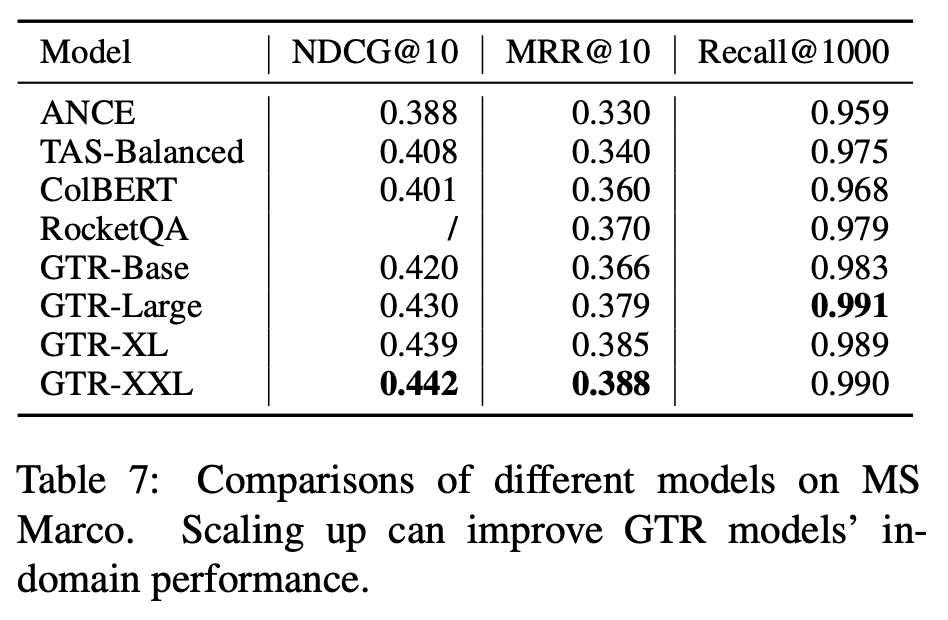
  • 위 테이블과 아래 테이블에서 확인할 수 있듯이 계속 좋아진다.
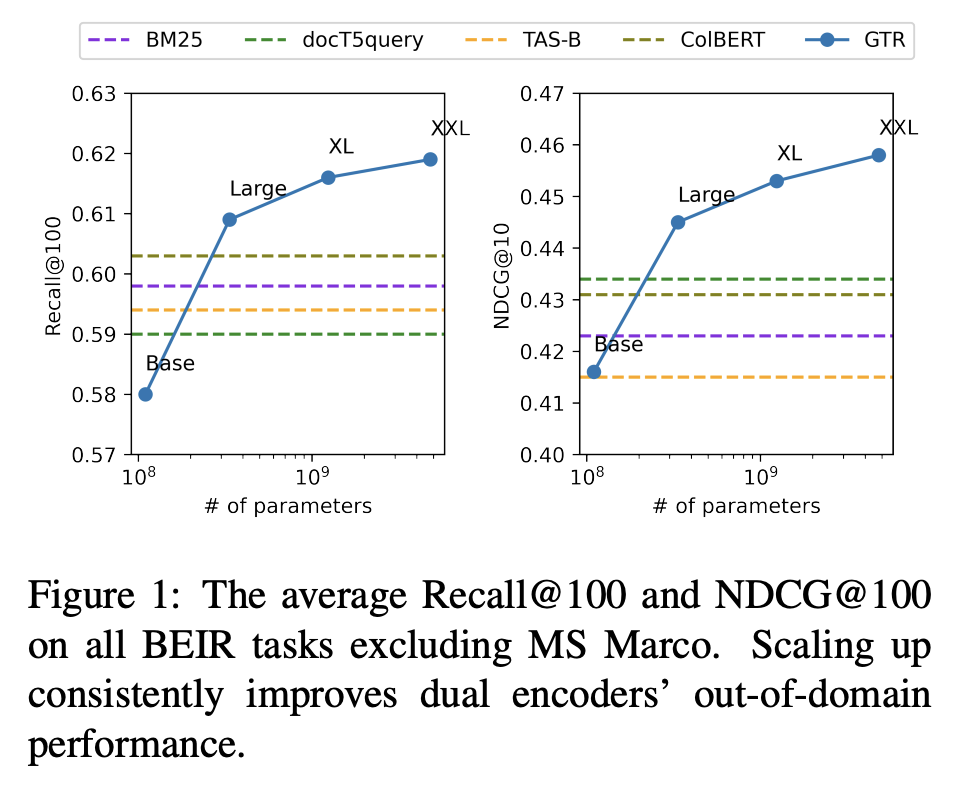
• Out-of domain generalization
  • GTR-large sota
  • 모델 커질수록 점수가 좋아짐.
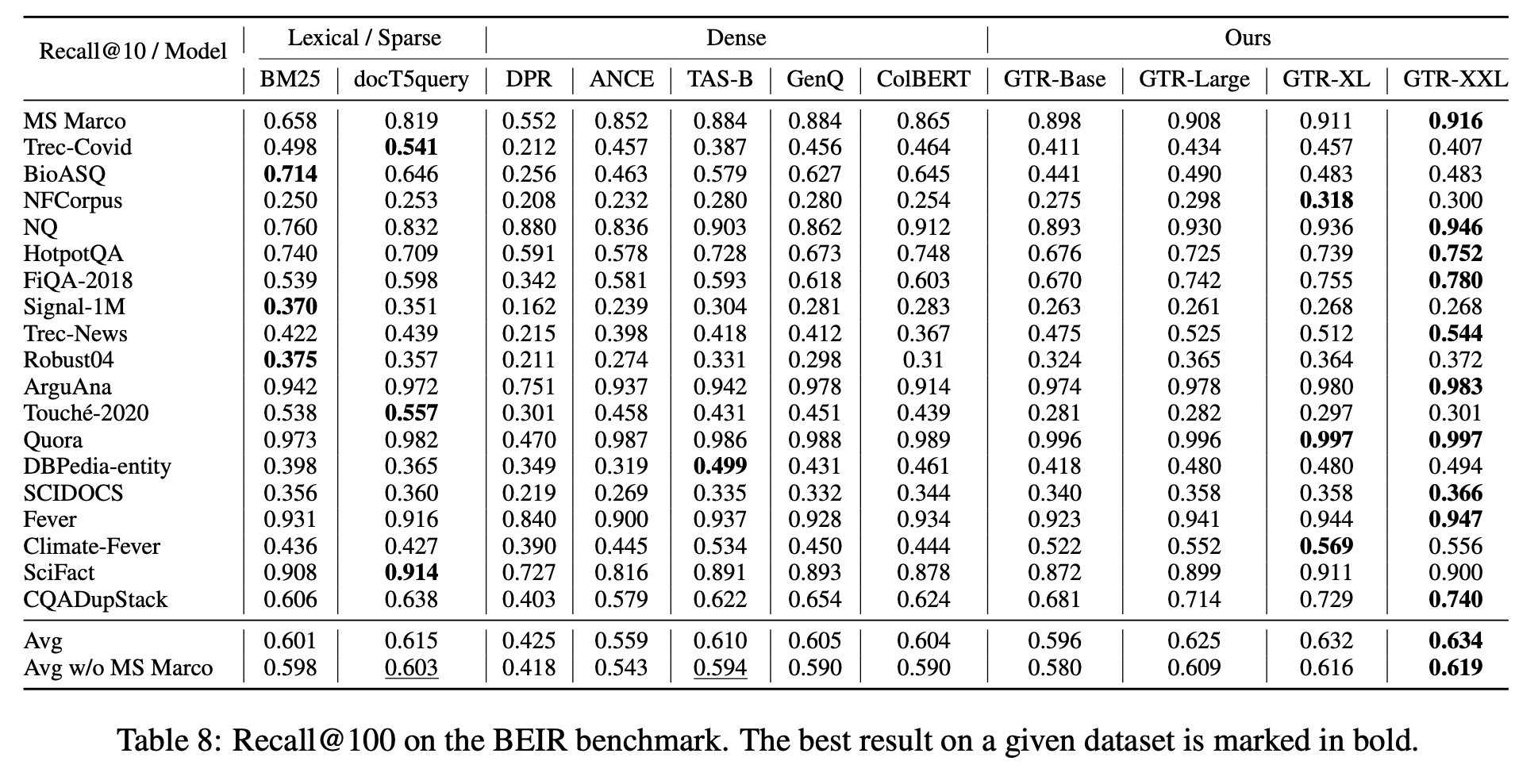
  • generalization을 위해서 스케일을 올리는 것은 반드시 필요하다.

Abalation

• GTR : Pre-training stage + Fine-tuning stage
• GTR-RT : Fine-tuning stage
• GTR-PT : Pre-training stage

Data efficiency

• In-domain, Out-of-domain 나누어 10%의 데이터만 사용한 결과를 보면
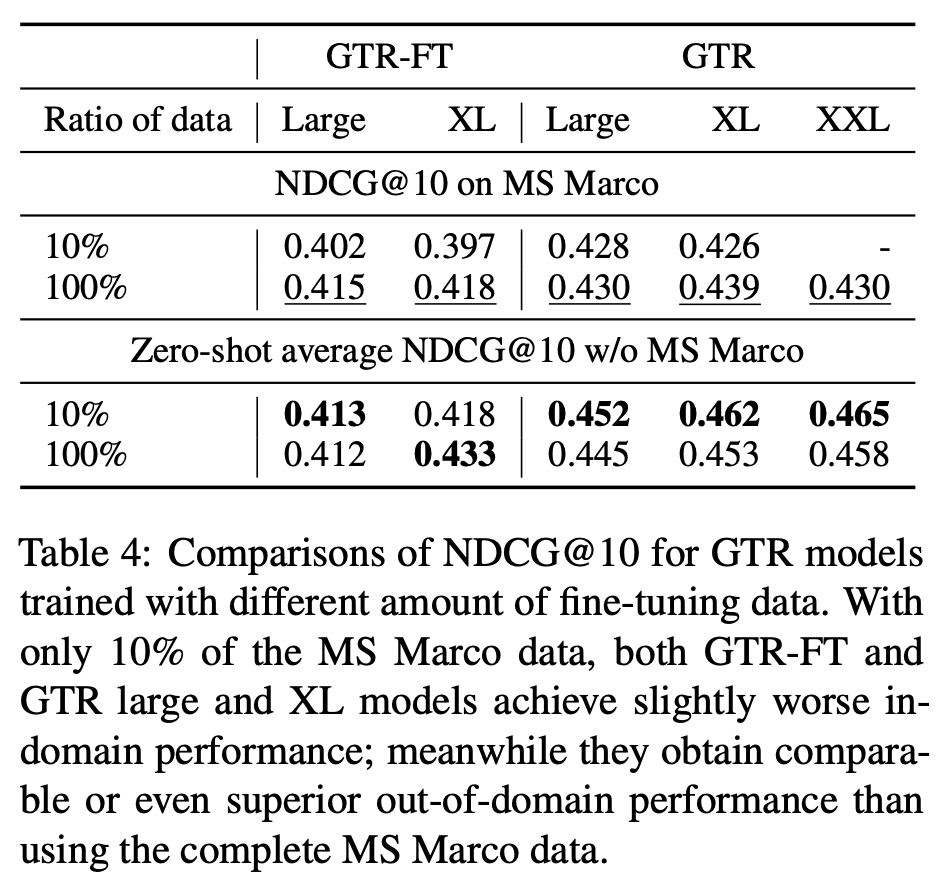
  • In-domain에서는 10%만 사용할 때에 비해 100% 데이터를 사용한 결과가 좋았다.
  • Out-of-domain에서는 들쭉날쭉한 결과를 보이기도 하며(GTR-FT), 심지어 GTR 모델의 경우 10%만의 데이터로 훈련했을 때의 결과가 더 좋았다.

Scaling up

• In-domain, Out-of-domain 결과를 나누어보면
  
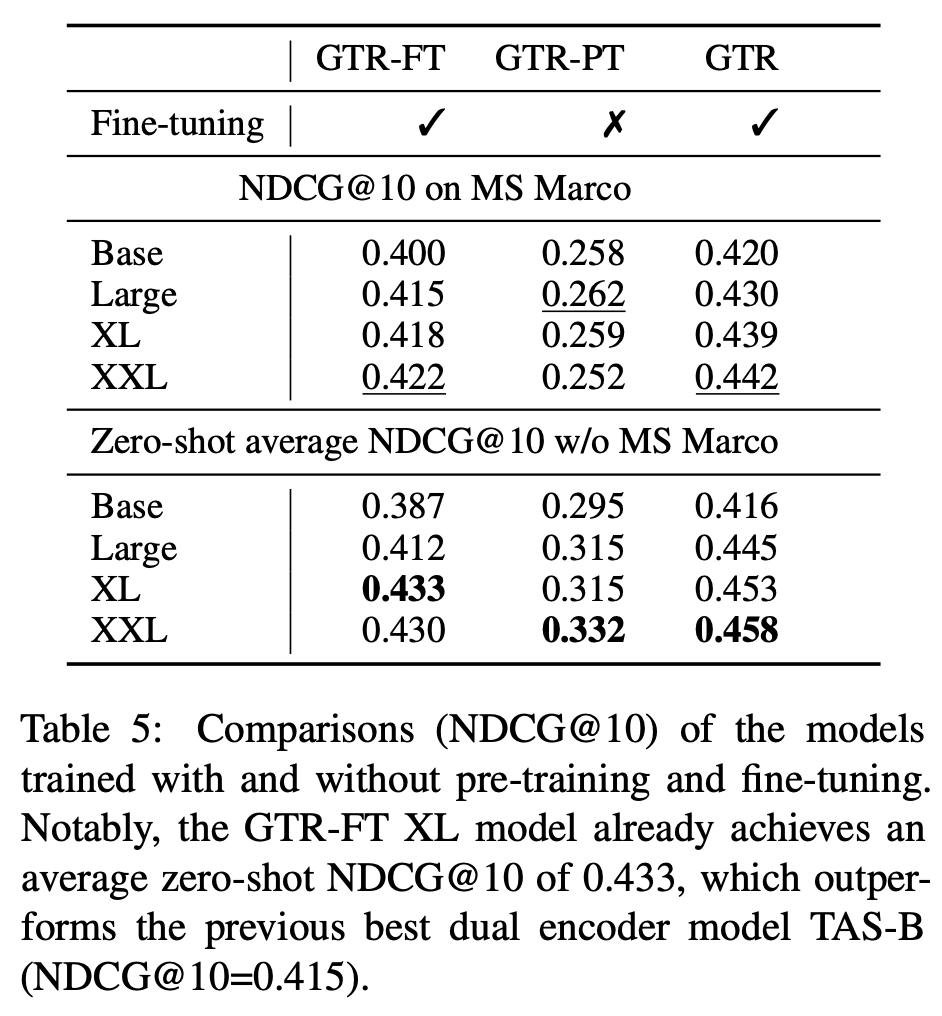
  • GTR-PT 에서는 특히 In-domain에서 모델이 커짐으로써 점수가 커지지는 않는다.
  • GTR-FT 경우 out-of-domain에서는 XXL이 XL 보다 점수가 낮지만 in-domain에서는 점수가 증가한다.
  • GTR 모델의 경우 두 가지 케이스에서 스케일이 커짐에 따라 점수가 증가한다.
  • 결과적으로 GTR 모델의 경우 두 상황에서 scale up이 점수향상에 도움이 되는 것을 분명하게 확인할 수 있다.

Fine-tuning data

• NQ 데이터의 경우 위키피디아 document로 구성되어 있으며 MSMARCO와 비교했을 때 사이즈도 작다.
• DPR 모델이 NQ로 finetuning 되었다는 점을 감안했을 때에 GTR-Base와 비교해볼 수 있다.
  
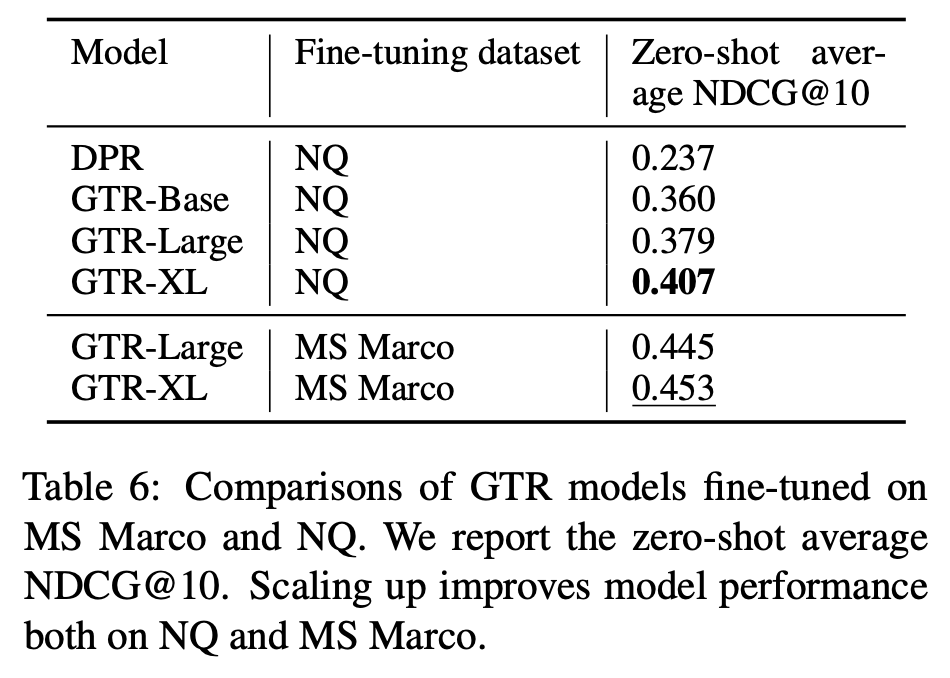
  • DPR(NQ), GTR-Base(NQ) 비교하면, 두 모델의 차이점이 backbone 모델이 다르다는 점인데, 이 둘이 크게 차이가 나지 않는다는 가정에서는 GTR-Base에서 Pre-training stage가 효과적이라고 말할 수 있다.
  • NQ 데이터셋에서도 모델이 커짐에 따라 점수가 계속해서 향상된다. (특히 GTR-Large, GTR-XL의 차가 크다. 이 연구에서는 weaker finetuning data의 경우 스케일을 키우는게 더 도움이 된다고 해석하고 있음.)

질문

• 아래와 같은 수치를 보면 NDCG와 MRR이 있는데 NDCG가 더 높은게 가능할까?
  

  • NDCG는 검색 결과의 정확도와 상대적인 순서를 모두 고려하므로, MRR보다 더 강력한 지표인 것이 맞다. 하지만 아래 계산을 참고하면 가능할 것으로도 보인다.

    1번째: MRR@10 = 1/1 = 1.0
    2번째: MRR@10 = 1/2 = 0.5
    3번째: MRR@10 = 1/3 ≈ 0.3333
    4번째: MRR@10 = 1/4 = 0.25
    5번째: MRR@10 = 1/5 = 0.2
    6번째: MRR@10 = 1/6 ≈ 0.1667
    7번째: MRR@10 = 1/7 ≈ 0.1429
    8번째: MRR@10 = 1/8 = 0.125
    9번째: MRR@10 = 1/9 ≈ 0.1111
    10번째: MRR@10 = 1/10 = 0.1

    각 순위에 대한 NDCG@10 값을 구하려면 정답의 중요도를 알아야 하지만, 중요도가 모두 1이라고 가정하면

    1번째: NDCG@10 = DCG@10 = 1/1 = 1.0
    2번째: NDCG@10 = DCG@10 = 1/(1 + log2(2)) ≈ 0.6309
    3번째: NDCG@10 = DCG@10 = 1/(1 + log2(3)) ≈ 0.5211
    4번째: NDCG@10 = DCG@10 = 1/(1 + log2(4)) ≈ 0.4307
    5번째: NDCG@10 = DCG@10 = 1/(1 + log2(5)) ≈ 0.3614
    6번째: NDCG@10 = DCG@10 = 1/(1 + log2(6)) ≈ 0.3057
    7번째: NDCG@10 = DCG@10 = 1/(1 + log2(7)) ≈ 0.2604
    8번째: NDCG@10 = DCG@10 = 1/(1 + log2(8)) ≈ 0.2231
    9번째: NDCG@10 = DCG@10 = 1/(1 + log2(9)) ≈ 0.1911
    10번째: NDCG@10 = DCG@10 = 1/(1 + log2(10)) ≈ 0.1633

• NDCG 계산하기 예제

  문서 1: 중요도 0.8, 순위 2
  문서 2: 중요도 0.5, 순위 1
  문서 3: 중요도 0.2, 순위 3

  DCG 계산:
  DCG@3 = 중요도1/(1 + log2(순위1)) + 중요도2/(1 + log2(순위2)) + 중요도3/(1 + log2(순위3))
  DCG@3 = 0.5/(1 + log2(1)) + 0.8/(1 + log2(2)) + 0.2/(1 + log2(3))

  DCG@3 ≈ 0.5 + 0.8/(1.585) + 0.2/(2)

  DCG@3 ≈ 0.964

  Ideal DCG 계산:
  Ideal DCG@3는 모든 문서를 정확한 순서대로 나열했을 때의 DCG 값
  Ideal DCG@3 = 중요도1 + 중요도2 + 중요도3

  Ideal DCG@3 = 0.8 + 0.5 + 0.2

  Ideal DCG@3 = 1.5

  NDCG 계산:
  NDCG@3 = DCG@3 / Ideal DCG@3
  NDCG@3 = 0.964 / 1.5

  NDCG@3 ≈ 0.6427