FBX Parsing / CPU Skinning

happyhour·2025년 7월 10일

C++DirectX11 FBX Skinning animation d3d11 게임테크랩

DirectX11

목록 보기

2/4

캐릭터 애니메이션 - FBX와 CPU Skinning

개요

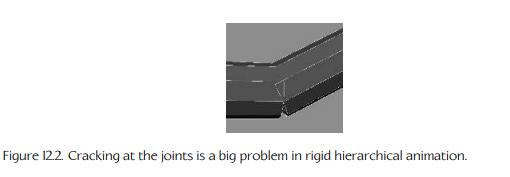
둠 등의 초기 3D 게임들이 사용한 스프라이트 애니메이션 기법은 3D 그래픽 시대가 되며 계층적 강체 애니메이션으로 발전되어, 여러 강체(단단한 물체)의 모음으로 모델링하게 됩니다. 포유류의 뼈들이 관절로 서로 연결돼 있는 것과 비슷한 식으로 강체들은 다른 강체들과 계층적으로 이어져 있기 때문에 캐릭터를 자연스럽게 움직일 수 있습니다.

계층적 강체 애니메이션은 관절에서 강체들이 갈라져 보여 부자연스럽다는 문제점이 있으며, 기계들을 나타내는 데에는 부족함이 없지만 육신을 가진 캐릭터를 나타내기에는 부족한 점이 있습니다.

이 문제를 해결하기 위해 각 정점들을 따로 움직여 모양이 자연스럽게 펴지게 할 방법으로, “정점 애니메이션”이란 우악스러운 방법이 등장합니다. 모든 메시의 각 정점이 시간에 따라 어떻게 변하는지 모두 기록하는 방법인데요, 당연히 데이터는 굉장히 커지고 실시간 게임에서 활용하기에는 무리가 있습니다.

(위 방법의 일종인 ‘모프 타깃 애니메이션’ 기법은 대개 표정 애니메이션에 이용되어, 50개 이상의 근육으로 구성된 사람의 얼굴을 표현합니다.)

Skinned Animation - 스킨 애니메이션

메시 정점 모양을 변화시키면서도 속도가 빠르고, 메모리 사용량이 적은 Skinned Animation(스킨 애니메이션)기법은 피부나 의복을 그럴싸하게 흉내낼 수 있는 기법입니다.

초기 ‘슈퍼 마리오 64’같은 게임에서 사용된 위 기법은 현재에도 유명 캐릭터의 전 부위 또는 일부분에라도 사용되는 기법입니다. (솔리드 스네이크, 드레이크, 버즈 라이트 이어, 조엘 등..)

단단한 뼈(Bone)들로 이뤄진 뼈대(Skeleton)을 만든 후, 스킨(Skin)이라 불리는 이어진 삼각형들로 이뤄진 메시가 뼈대의 관절로에 붙고, 스킨의 각 정점들은 관절의 움직임을 따라갑니다. 각 정점들은 여러 관절에 가중치를 갖고 붙을 수 있는데, 이렇게 하면 영향받는 뼈(Bone)를 따라 뼈에 붙은 스킨이 마치 사람 뼈에 붙은 피부처럼 자연스럽게 따라갈 수 있게 됩니다.

Skeleton Hierarchy - 뼈대 계층 구조

뼈대 관절들은 계층 구조나 트리 구조로 이뤄져 있으며, 통상 1개의 루트 관절을 시작으로 나머지 관절들이 바로 밑의 자식 또는 자식의 자식이 되는 식으로 붙게 됩니다.

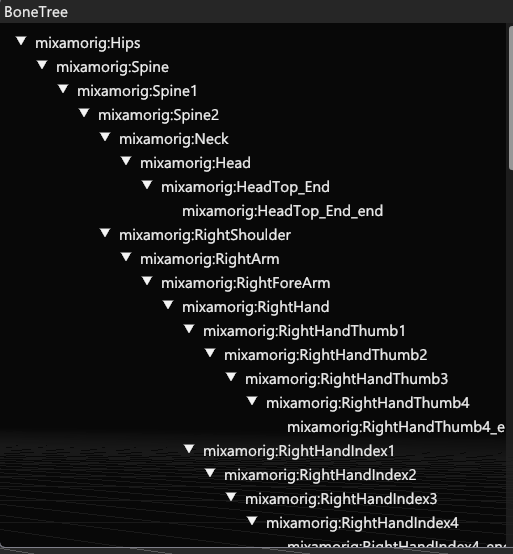
뼈대를 자료 구조로 나타낼 때는 각 관절 자료 구조들을 배열로 갖는 형태로 경우가 많은데요, 언리얼의 경우 FReferenceSkeleton 클래스 내에 각 관절들의 정보를 TArray 배열로 담습니다.

관절 인덱스(Joint Index)는 애니메이션 자료 구조 안에 있는 관절들을 가리키는 번호로써, 예를 들어 0번은 루트를 나타내고, 자식 관절에서 부모 관절을 가리킬 때 부모의 관절 인덱스를 사용해 나타내기도 합니다.

마찬가지로 스킨을 구성하는 삼각형 메시의 정점은, 자신이 따라 움직일 관절을 관절 인덱스를 사용하여 나타내어, 해당 관절 인덱스로 관절의 트랜스폼과 가중치의 곱을 누적합시키는 방식으로 위치를 계산합니다.

관절 인덱스를 사용하면 관절 이름을 사용할 때보다 필요한 저장 공간이 줄어들고(256개의 관절을 나타내기 위해 필요한 비트수는 8비트입니다), 배열 인덱스로 바로 접근할 수 있어 빠르다는 장점이 있습니다.

Bind Pose - 바인드 포즈

바인드 포즈란 처음 관절과 스킨 메시의 정점들을 연결 지을 때 관절의 위치, 방향, 스케일을 뜻합니다. 보통 이 변환의 역인 역바인드 행렬을 저장하는데, 이는 예를 들어 월드 공간에서 각 메시의 삼각형 정점이 회전하더라도 해당 정점들이 속한 관절들에 대한 상대적 관계는 불변하기 때문입니다. (후술)

용어 정리

글로벌 포즈 (Joint-to-Model Transform)

관절 j의 글로벌 좌표계에서 모델 좌표계로의 변환 행렬은 모든 부모 조인트의 변환을 누적해서 구할 수 있습니다.

예를 들어, 관절 2와 관절 5의 글로벌 포즈는 각각 아래 수식으로 계산할 수 있습니다.

\mathbf{P}_{2 \rightarrow M} = \mathbf{P}_{2 \rightarrow 1} \mathbf{P}_{1 \rightarrow 0} \mathbf{P}_{0 \rightarrow M}

\mathbf{P}_{5 \rightarrow M} = \mathbf{P}_{5 \rightarrow 4} \mathbf{P}_{4 \rightarrow 3} \mathbf{P}_{3 \rightarrow 0} \mathbf{P}_{0 \rightarrow M}

즉, 일반화된 형태로 관절 j의 글로벌 포즈는 다음과 같이 표현됩니다.

\mathbf{P}_{j \rightarrow M} = \prod_{i=j}^{0} \mathbf{P}_{i \rightarrow p(i)}

여기서 p(i)는 관절 i의 부모 관절 인덱스입니다.

바인드 포즈와 현재 포즈

바인드 포즈에서의 변환 행렬:

관절 j의 바인드 포즈 변환 행렬의 역행렬을 이용하여 바인드 공간의 정점 v_j^B을 모델 공간으로 변환합니다

\mathbf{B}_{M \rightarrow j} = (\mathbf{B}_{j \rightarrow M})^{-1} \\ \mathbf{v}_j = \mathbf{v}_M^B \mathbf{B}_{M \rightarrow j} = \mathbf{v}_M^B (\mathbf{B}_{j \rightarrow M})^{-1} \tag{12.3}

현재 포즈에서의 변환 행렬:

조인트의 현재 포즈를 나타내는 행렬 Cj→M를 사용하여 다시 모델 공간으로 변환합니다

\mathbf{v}_M^C = \mathbf{v}_j \mathbf{C}_{j \rightarrow M}

위 두 수식을 조합하면, 바인드 포즈에서 현재 포즈로 직접 변환하는 수식을 다음과 같이 얻을 수 있습니다

\mathbf{v}_M^C = \mathbf{v}_j \mathbf{C}_{j \rightarrow M} \\ = \mathbf{v}_M^B (\mathbf{B}_{j \rightarrow M})^{-1} \mathbf{C}_{j \rightarrow M} \\= \mathbf{v}_M^B \mathbf{K}_j \tag{12.4}

이 때, 위의 Kj는 바인드 포즈와 현재 포즈 간의 결합 변환이며, 이를 스키닝 행렬 (Skinning Matrix)라고 부릅니다

\mathbf{K}_j = (\mathbf{B}_{j \rightarrow M})^{-1} \mathbf{C}_{j \rightarrow M}

Multiple Joing Skinning (블렌딩)

정점 하나가 여러 개 관절에 의해 영향을 받을 때 각 관절로 스키닝된 결과를 가중합(weighted sum)으로 결합됩니다.(가중치 합 = 1) 즉, 관절 별로 독립적으로 계산된 결과를 관절의 가중치를 기준으로 Blending한다 하여, LBS (Linear Blend Skinning)이라 부릅니다.

조인트 인덱스: j0∼jN−1
가중치: w0∼wN−1
각 조인트의 스키닝 매트릭스: Kji
바인드 포즈에서의 정점: vMB

최종 변환된 정점 좌표는 다음과 같이 계산됩니다:

\mathbf{v}_M^C = \sum_{i=0}^{N-1} w_i \, \mathbf{v}_M^B \, \mathbf{K}_{j_i}

Model Space to World Space Transformation - 모델 공간에서 월드 공간으로

최종적으로 정점을 모델 공간 → 월드 공간으로 변환하기 위해, 아래와 같이 계산하여 필요한 행렬 곱셈 수를 줄일 수 있습니다.

(\mathbf{K}_j)_W = (\mathbf{B}_{j \rightarrow M})^{-1} \, \mathbf{C}_{j \rightarrow M} \, \mathbf{M}_{M \rightarrow W}

Unreal Engine Skinning

FBX SDK를 이용하여 USkeletalMesh가 저장할 Raw Data, Reference Skeleton, Render Data를 파싱할 텐데요, 이에 앞서 언리얼 엔진 5에서는 어떤 구조로 관련 정보를 저장하고 소유관계에 있는지 간단히 짚어보겠습니다.

자료 구조 설명

FSkeletalMeshLODModel

에디터에서 메시의 정점·인덱스·웨이트 같은 “원시(raw) 데이터”만 담음
- 실제 GPU/CPU 스키닝에 필요한 역바인드 행렬(inv-bind matrix)이나 파이프라인용 최적화 행렬은 런타임 리소스 쪽에 따로 만들어서 보관

FSkeletalMeshRenderData

LOD 당 렌더링용 리소스

FTransform의 3가지 종류

레퍼런스 포즈 트랜스폼 (Reference Pose Transform)

의미
- 모델이 “바인드된” 기본 자세, 즉 T-포즈나 스킨 바인딩 시점의 본(뼈) 위치·회전·스케일을 FTransform으로 표현한 것
저장 위치
- 에셋 차원에서 USkeletalMesh::RefSkeleton 내부
- 구체적으로 FReferenceSkeleton::GetRefBonePose()가 반환하는 TArray<FTransform> RefBonePose
이유
- 메시(asset) 자체가 처음 설계된 바인드 포즈 정보를 가져야 하므로 골격 소유 클래스로 보관

역바인드 매트릭스 (Inverse Bind Matrix)

의미
- “바인드 포즈”에서 본이 메시를 스킨에 맞추기 위해 쓰였던 행렬(BindMatrix)의 역행렬.
- 런타임에 본의 현재 변환과 곱해서, 메시 공간 → 본 공간 → 다시 메시 공간으로 올바른 스키닝 좌표를 계산할 때 사용
저장 위치
- 메시 LOD 모델 단위로 FSkeletalMeshLODModel::RefBasesInvMatrix (TArray<FMatrix>)
이유
- 메시마다 바인드 포즈가 같더라도, LOD별 데이터(버텍스 수, 인덱싱 등)와 함께 묶어 관리하는 편이 성능·메모리 관점에서 유리
- 애셋 쿠킹 단계에 미리 계산해 두면, 런타임 성능 오버헤드를 줄일 수 있음

현재 본 트랜스폼 (Current Bone Transform)

의미
- 애니메이션 블루프린트나 시퀀서 실행 중에 계산된, 컴포넌트 공간(Component Space) 상의 본 위치·회전·스케일
- FTransform 형태로 각 본마다 매 프레임 업데이트
저장 위치
- 런타임 컴포넌트 차원인 USkinnedMeshComponent (또는 FAnimInstanceProxy) 내부
- 멤버 TArray<FTransform> ComponentSpaceTransforms 에 보관
이유
- 인스턴스마다(캐릭터마다) 애니메이션 상태가 다르므로, 에셋과 분리해 컴포넌트·애니메이션 레벨에서 관리

런타임 본 트랜스폼과 바인드 포즈 정보 분리 이유

에셋 내 바인드 정보(RefBonePose, RefBasesInvMatrix)는 메시 구조와 긴밀히 묶여 있고 변하지 않으므로 에디터 단계에 계산해 두는 게 효율적

런타임 본 트랜스폼은 매 인스턴스·매 프레임 변경되므로, CPU 스키닝 루프가 빠르게 참조할 수 있는 컴포넌트 영역에 보관

이렇게 구분해 두면, 애셋 로딩과 스키닝 계산 모두 최적화된 메모리 레이아웃과 계산 흐름으로 처리할 수 있습니다.

구현 설명

FBX Parsing via SDK

FBX에서 파싱한 정보를 어떻게 CPU Skinning에 불러들이고, 어떻게 파싱하였는지 기술합니다

ReferenceSkeleton / Inverse Bind Pose

각 FbxNode 트리를 순회하며, 각 Bone 노드에 대해 로컬 / 글로벌 트랜스폼을 저장합니다.

유의할 점으로는 FRotator 대신 FQuat으로 FTransform을 정의하여 혹시 있을 회전 축 정의 순서 오류를 방지한 것입니다.

RefBonePose → 글로벌 기준 포즈 저장
- InitializeInverseBindPose() → RefBasesInvMatrix = RefBonePose의 역행렬로 생성

void FFbxImporter::BuildReferenceSkeleton(FbxNode* Node, FReferenceSkeleton& OutRefSkeleton, uint32 ParentIndex, int32 Depth)
{
    if (Attr && Attr->GetAttributeType() == FbxNodeAttribute::eSkeleton)
    {
        FbxAMatrix Local = Node->EvaluateLocalTransform();
        FTransform LocalBonePose(
            FVector(Local.GetT()[0], Local.GetT()[1], Local.GetT()[2]) * 0.01f,
            FQuat(Local.GetQ()[0], Local.GetQ()[1], Local.GetQ()[2], Local.GetQ()[3]),
            FVector(Local.GetS()[0], Local.GetS()[1], Local.GetS()[2])
        );

        FbxAMatrix Global = Node->EvaluateGlobalTransform();
        FTransform GlobalBonePose(...);

        int32 ThisIndex = OutRefSkeleton.AddBone(BoneName, ParentIndex, LocalBonePose);
        OutRefSkeleton.RefBonePose.Add(GlobalBonePose);
    }
}

Skin Weight / Bone Influence

각 Mesh의 삼각형들에 대해 영향을 끼칠 인플루언스 정보입니다. 영향을 주는 Bone의 인덱스, 그의 가중치가 담겨져있으며 최대 MAX_TOTAL_INFLUENCES 개의 상위 가중치만 사용하도록 정렬하였습니다. (언리얼에서는 최대 8개까지 지원한다고 합니다.)

아래의 파싱 후, 총합 1이 되도록 가중치를 정규화 시켜주었습니다.

for (FbxSkin* Skin : Mesh->GetDeformerCount())
{
    for (FbxCluster* Cluster : Skin->GetClusterCount())
    {
        Cluster->GetControlPointIndices();   // 정점 인덱스
        Cluster->GetControlPointWeights();   // 가중치
        Cluster->GetLink();                  // 연결된 본 노드

        BindPoseMap[BoneIndex] = (Minitial^-1 * Mlink)^-1;
        LodModel.RequiredBones.Add(BoneIndex);
    }
}

정점(Vertex) 데이터

1개 Skeleton에 대해 여러 개의 FbxNode가 존재할 수 있기 때문에(대표적으로 Mixamo), RootNode의 모든 자식 노드를 DFS 탐색하며 모든 Node에 대한 Mesh 데이터를 파싱해야 합니다.

1개 FBX에 대한 1개의 Vertex Buffer, Index Buffer로 생성하기 위해서 시작 정점 인덱스, 인덱스 개수, 인덱스 오프셋 등을 알맞게 파싱하였습니다.

ControlPoints → 모델 공간 좌표
- Normal, Tangent, Binormal → LayerElement에서 직접 접근
- GeometricTransform 보정 적용

// FBX의 cm 좌표계 -> 언리얼의 m 좌표계 스케일링 적용 
FbxVector4 P = Geo.MultT(Mesh->GetControlPoints()[cp]);
V.Position = FVector(P[0], P[1], P[2]) * UnitScale; 

FbxVector4 n = normalLayer->GetDirectArray().GetAt(finalIdx);
V.TangentZ = FVector4(n[0], n[1], n[2], 0);

UV / Vertex Color / Material Index

특기할 점으로는 UV는 최대 MAX_TEXCOORDS로 정의된 개수 지원이 되며, Y축을 기준으로 뒤집어 줘야 한다는 점입니다. 머티리얼은 eByPolygon 매핑을 기준으로 사용하였습니다.

auto uv = uvElem->GetDirectArray().GetAt(finalIdx);
V.UVs[u] = FVector2D(uv[0], 1.f - uv[1]);

auto c = colorLayer->GetDirectArray().GetAt(finalIdx);
V.Color = FColor((uint8)(c.mRed * 255), ...);

materialLayer → matIdx
V.MaterialIndex = matIdx;

파싱 후 : Component / World Space TranfromArray - 본의 로컬 / 글로벌 트랜스폼

불필요한 복사일 수 있으나 가독성을 위해 따로 구분지어 각각 본의 로컬, 글로벌 트랜스폼과 원본 Vertex를 저장합니다. 주로 글로벌 트랜스폼 정보는 Skinning Matrix 연산에, 로컬 트랜스폼 정보는 부모 → 자식 노드들의 위치 업데이트에 사용되겠습니다.

void USkeletalMeshComponent::ResetBoneTransform()
{
    ComponentSpaceTransformsArray.Empty();
    WorldSpaceTransformArray.Empty();
    for (auto& Transform : SkeletalMesh->RefSkeleton.GetBonePose())
    {
        WorldSpaceTransformArray.Add(Transform);
    }
    for (auto& Bone : SkeletalMesh->RefSkeleton.GetBoneInfo())
    {
        ComponentSpaceTransformsArray.Add(Bone.LocalTransform);
    }
    SkeletalMesh->ImportedModel->Vertices.Empty();
    for (const auto& Vertex : BindPoseVertices)
    {
        SkeletalMesh->ImportedModel->Vertices.Add(Vertex);
    }
}

CPU Skinning

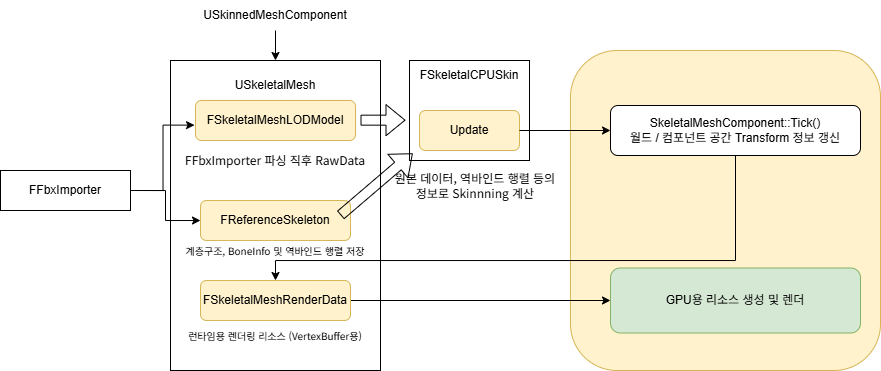
이렇게 파싱 과정을 거치면 USkeletalMesh에는 3가지 정보가 담기게 됩니다. CPU Skinning 옵션이 켜져 있을 때만, FSkeletalMeshCPUSkin::Update()를 호출해주어 원본 Vertex에 대한 Skinning 후의 위치, 노말, 탄젠트 등의 갱신 과정을 거칩니다.

참고로 해당 ~CPUSkin 클래스는 SkinnedMeshComponent에 소유된 클래스 포인터이자, 멤버 변수 USkeletalMesh에 접근할 수 있는 오직 CPU Skinning 연산용 클래스입니다.

Skinned Matrix 개요

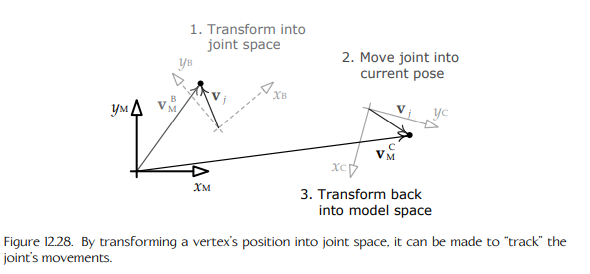
FBX 기반 Skeletal Mesh는 정점(Vertex) 정보를 바인드 포즈(Bind Pose) 기준으로 저장합니다.

CPU Skinning은 애니메이션에 따라 움직이는 본(Bone)의 위치에 맞춰 정점들을 재계산하는 과정입니다.

이를 위해 SkinnedMatrix는 다음과 같은 좌표 변환 역할을 합니다:

“정점을 바인드 포즈 기준 좌표계 → 현재 본 애니메이션 월드 위치로 보내는 변환자”

즉, SkinnedMatrix는 초기 바인드 포즈에 붙어 있던 정점을 현재 기준(애니메이션 적용 후 위치)로 보정해주는 선형 변환 행렬입니다.

연산 과정

TArray<FMatrix> InverseBindPose = Skeleton.GetInverseBindPose(); // [1] 정점 저장 기준 좌표계
TArray<FTransform> GlobalTransforms = InMeshComponent->GetWorldSpaceTransforms(); // [2] 현재 애니메이션된 본 위치

// [3] 각 본마다 SkinnedMatrix 계산
for (int32 b = 0; b < NumBones; ++b)
{
    FMatrix BoneM = GlobalTransforms[b].GetMatrix();  // 현재 본의 위치 (본 → 월드)
    SkinnedMatrices[b] = InverseBindPose[b] * BoneM;  // 바인드기준 → 현재본 위치로 변환
}

이렇게 계산된 Skinned Matrix는 각 버텍스 별로 영향받는 Bone이 존재할 때만 연산에 개입하게 됩니다. 즉, 가중치를 곱하여 영향을 준 Bone은 원본 정점에 대해 원본 바인드 포즈 공간(모델 공간) → 월드 공간 변환을 수행하는 셈입니다.

실제 스키닝 관련 코드는 아래와 같이 누적시켜 정점 정보를 갱신합니다.

for (int i = 0; i < MAX_TOTAL_INFLUENCES; ++i)
{
    float W = Src.InfluenceWeights[i];
    int Bi = Src.InfluenceBones[i];
    const FMatrix& M = SkinnedMatrices[Bi];

    Psum += M.TransformPosition(Src.Position) * W;
    Nsum += M.TransformFVector4(Src.TangentZ) * W;
    Tsum += FMatrix::TransformVector(Src.TangentX, M) * W;
}

위 코드에 대한 단계를 표로 정리하면..

단계	수학적 표현	의미
1. 정점	`v_orig`	본 바인드포즈 기준 좌표
2. 바인드 → 메시	`v_m = InverseBindPose × v_orig`	메시 공간으로 변환
3. 메시 → 현재 본 위치	`v_final = GlobalTransform × v_m`	애니메이션된 위치로 이동
4. 축약	`v_final = (InvBindPose × Global) × v_orig`	즉, `SkinnedMatrix × v_orig`

아래 코드에선 자료를 참고하여 행렬 곱셈을 최소화하도록 구현했습니다.

Skinning 관련 전체 코드

void FSkeletalMeshObjectCPUSkin::Update(USkinnedMeshComponent* InMeshComponent, float DeltaTime)
{
    // 1. SkeletalMeshRenderData에서 Vertices, Indices 가져오기
    // 2. ComponentSpaceTransformsArray에서 Bone Transform 가져오기
    // 3. Vertex를 Bone Transform에 맞게 변환
    // 4. 변환된 Vertex를 Weight를 적절히 적용하여 Skinning을 구현할 것   

    USkeletalMesh* SkeletalMesh = InMeshComponent->GetSkeletalMesh();
    FReferenceSkeleton& Skeleton = SkeletalMesh->RefSkeleton;
    TArray<FMatrix> InverseBindPose = Skeleton.GetInverseBindPose();
    TArray<FTransform> GlobalTransforms = InMeshComponent->GetWorldSpaceTransforms();

    // 1) 역바인드포즈 × 본글로벌행렬 합성 → SkinnedMatrices 에 저장
    const int32 NumBones = InverseBindPose.Num();
    TArray<FMatrix> SkinnedMatrices;
    SkinnedMatrices.SetNum(NumBones);
    for (int32 b = 0; b < NumBones; ++b)
    {
        FMatrix BoneM = GlobalTransforms[b].GetMatrix();
        SkinnedMatrices[b] = InverseBindPose[b] * BoneM;
    }

    const TArray<FSoftSkinVertex>& Vertices = InMeshComponent->GetBindPoseVertices();
    TArray<FSkeletalMeshVertex>& RenderDataVertices = SkeletalMesh->GetRenderData()->Vertices;

    const int32 NumVerts = Vertices.Num();
    for (int32 i = 0; i < NumVerts; ++i)
    {
        SkinVertexOptimized(Vertices[i],
            SkinnedMatrices,
            RenderDataVertices[i]);
    }
}
void FSkeletalMeshObjectCPUSkin::SkinVertexOptimized(
    const FSoftSkinVertex& Src,
    const TArray<FMatrix>& SkinnedMatrices,
    FSkeletalMeshVertex& Out)
{
    // 누적 변수
    FVector   Psum(0, 0, 0);
    FVector4  Nsum(0, 0, 0, 0);
    FVector   Tsum(0, 0, 0);

    // 각 인플루언스마다 미리 계산된 합성행렬만 사용
    for (int i = 0; i < MAX_TOTAL_INFLUENCES; ++i)
    {
        const float W = Src.InfluenceWeights[i];
        if (W <= KINDA_SMALL_NUMBER) continue;

        const int   Bi = Src.InfluenceBones[i];
        const FMatrix& M = SkinnedMatrices[Bi];

        Psum += M.TransformPosition(Src.Position) * W;
        Nsum += M.TransformFVector4(Src.TangentZ) * W;
        Tsum += FMatrix::TransformVector(Src.TangentX, M) * W;
    }

    // 결과 정규화 후 아웃풋에 복사
    Out.X = Psum.X;  Out.Y = Psum.Y;  Out.Z = Psum.Z;

    FVector N = FVector(Nsum.X, Nsum.Y, Nsum.Z).GetSafeNormal();
    Out.NormalX = N.X;  Out.NormalY = N.Y;  Out.NormalZ = N.Z;

    FVector T = Tsum.GetSafeNormal();
    Out.TangentX = T.X;  Out.TangentY = T.Y;  Out.TangentZ = T.Z;
}

Linear Blend Skinning

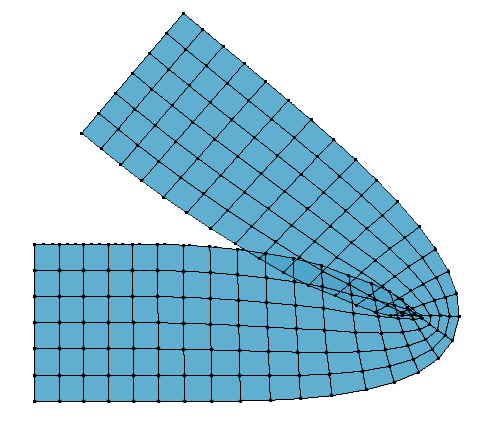
위에서 수행한 LBS 방식은 Candy Wrapping 현상이라 불리는 볼륨이 보존되지 않고 쪼그라드는 현상을 일으킵니다. 이는 선형 보간의 한계라 볼 수 있습니다.

Candy Wrapping 현상의 이유

LBS(Linear Blend Skinning) 은 각 본의 4×4 변환 행렬 Ti 을 가중합하여
$T_{\text{blend}} \;=\; \sum_i w_i \, T_i, \quad \sum_i w_i = 1$
로 버텍스 v 에 적용합니다.
1. 회전과 이동이 독립적으로 선형 보간하는 과정에서 중간에 shear(비틀림) 발생하고,
2. 뼈가 크게 꺾일 때 관절 부근이 부피가 움푹 꺼지는(volume loss) 현상이 생깁니다.
  
  이는 고유값 구조(회전축 보존)과도 연관이 있는데요,
  
  LBS는 회전행렬을 선형 보간함
  $M = \sum_{i} w_i R_i$
- 각 Ri: 회전 행렬 → 고유값: λ=1,e±iθ 이나,
  - 하지만 M은 더 이상 회전행렬이 아니기 때문에 고유값 구조가 깨지게 됩니다.
  - 즉, 각 회전행렬에 대한 고유벡터들이 다르면 LBS의 결과는 각 고유벡터들의 중간 또는 아무방향이 아니게 됩니다.
  - (고유벡터끼리 선형 보간한다고 해도 단일 고유벡터가 보존되지 않습니다.)
  
  즉, 선형 보간 자체가 고유값 구조(회전축 보존)를 무너뜨립니다. 이는 회전이 선형 공간이 아닌데 단순 가중합을 처리하는 데에서 비롯된 현상으로, 왜곡되어 비틀림, 축소 등의 Candy Wrapping 현상으로 이어집니다.

Dual Quaternion

회전의 특성(정규 직교) 및 시어 없음을 유지하면서도, 회전과 이동을 자연스럽게 결합하여 LBS의 부피 비보존 / 시어 현상을 보완한 것이 Dual Quaternion입니다.

개요

회전 성분과 이동 성분을 각각 쿼터니언으로 나눈 다음 하나의 구조로 처리하고, 정점 기준으로 자연스럽게 보간하기 위해 쓰인 것이 Dual Quaternion입니다. 기존 쿼터니언과 다른 점을 수식으로 표현해보겠습니다.

Quaternion q=3D 회전을 표현하는 4차원 단위벡터 $q = (r, \mathbf{u})$
Dual Quaternion = ‘실수부’와 ‘듀얼부’를 갖는 8차원 구조체
$\hat q \;=\; q_r \;+\; \varepsilon\,q_d, \quad \varepsilon^2 = 0$
- qr : 순수 회전(quaternion)
  $q_d = \tfrac12\,\mathbf{t}\,q_r$
  - qd = 회전 qr 뒤에 오는 이동 벡터 t
위 조합으로 Rigid Transform (회전+이동)을 표현

보완점

정규 직교 행렬의 특성을 가지는 회전 행렬을 선형 보간하면 이 특성이 깨진 것이 LBS였지요. Dual Quaternion은 회전을 비선형 보간(Sclerp)로 처리하여, 항상 순수 회전을 유지하여 정규 직교 조건을 유지시키게 됩니다.

또한 LBS는 결과적으로 행렬에 시어(shear)에 포함될 수 있는데요,(사각형이 평행사변형으로 찌그러진다던지) 시어를 표현하지 못하는 순수 회전 + 이동 표현만 갖기 때문에 시어가 발생하지 않는다는 장점이 있습니다.

특히, 단위 쿼터니언을 보간하며 정규화를 유지하므로 부피가 일정하게 유지됩니다.

LBS의 회전 왜곡으로 인한 부피 변화는 관절 회전이 큰 부위일수록 쪼그라들거나, 부풀어오르는 현상으로 나타납니다. Norm(노름)이 1인 쿼터니언 공간에서 보간하므로 스케일 정보가 새로 생기지 않기 때문에, Dual Quaternion은 볼륨을 보존할 수 있다는 장점이 있습니다.

연산 과정

본의 Rigid Transform (Ri, ti)를 듀얼 쿼터니언으로 표현합니다.

q_{r,i} = \bigl(\cos\frac\theta2,\;\sin\frac\theta2\,\mathbf{axis}\bigr), \quad q_{d,i} = \tfrac12\, (0,\mathbf{t}_i)\;*\;q_{r,i}.

가중합
$\widehat Q = \sum_i w_i\;\bigl(q_{r,i} + \varepsilon\,q_{d,i}\bigr).$
정규화 (Normalization)
$\widehat Q_{\text{norm}} = \frac{\widehat Q}{\|\widehat Q\|}$
버텍스 변형

\hat v = (0,\,\mathbf v), \qquad \hat v' = \widehat Q_{\text{norm}}\;\hat v\;\widehat Q_{\text{norm}}^*.

이후 결과 벡터 v’를 추출하여 왜곡이 덜한 정점 위치를 추출합니다.

스키닝 관련 수식

각 본의 최종 변환
$M_i = M_{\text{global}}^i \cdot (M_{\text{bind}}^i)^{-1}$
- 글로벌 트랜스폼과 바인드포즈 역행렬을 곱하여 스키닝 행렬을 구함
해당 행렬을 쿼터니언+이동 벡터로 변환 → DQi
각 정점에 대해 dual quaternion을 가중치로 선형 결합
$DQ_{\text{blend}} = \sum_{i=0}^{n} w_i \cdot DQ_i$
- 단, DQi는 hemisphere correction이 필요
정규화 후, 정점 위치/노말/탄젠트를 변환:v′=DQblend⋅v⋅DQblend−1 $v' = DQ_{\text{blend}} \cdot v \cdot DQ_{\text{blend}}^{-1}$

코드 설명

각 본에 대해

합성 행렬 M=InvBindPose×GlobalTransform 계산
M 에서 회전 부분은 FQuat(M) 으로, 이동 부분은 M.GetOrigin() 으로 분리
이를 FDualQuat(Rot, Trans) 생성자에 넣어 듀얼 쿼터니언 객체로 만들고
.GetNormalized() 로 단위화(Norm=1)

for (int32 b = 0; b < NumBones; ++b)
{
    // 1) 합성 행렬 계산
    FMatrix M = InverseBindPose[b] * GlobalTransforms[b].GetMatrix();

    // 2) 회전·이동 분해
    FQuat   Rot   = FQuat(M);
    FVector Trans = M.GetOrigin();

    // 3) 듀얼 쿼터니언 생성 & 정규화
    SkinDQs[b] = FDualQuat(Rot, Trans).GetNormalized();
}

버텍스별 DQ 블렌딩

각 버텍스마다:

영향 본(InfluenceBones) 과 가중치(InfluenceWeights)를 읽어옴
첫 번째 유효 가중치로 BlendedDQ 를 초기화
이후 가중치가 있는 모든 본에 대해
- 사인 정렬(Sign correction): 첫 쿼터니언과 반구(hemisphere)가 맞지 않으면 부호를 반전
- w * CurrentBoneDQ 를 BlendedDQ 에 누적
가중치 합(TotalWeight)으로 나눠 평균화
.Normalize() 호출로 최종 단위듀얼쿼터니언 확보

FDualQuat BlendedDQ = {/* Real=0, Dual=0 */};
float TotalWeight = 0.f;
FQuat  FirstRealQuat;
bool   bFirst = true;

for (int i = 0; i < MAX_TOTAL_INFLUENCES; ++i)
{
    float w = Src.InfluenceWeights[i];
    if (w <= KINDA_SMALL_NUMBER) continue;
    int bi = Src.InfluenceBones[i];
    FDualQuat DQ = SkinDQs[bi];

    if (bFirst)
    {
        FirstRealQuat = DQ.Real;
        BlendedDQ.Real = DQ.Real * w;
        BlendedDQ.Dual = DQ.Dual * w;
        bFirst = false;
    }
    else
    {
        // 3-1) Sign correction
        if (FQuat::DotProduct(FirstRealQuat, DQ.Real) < 0)
        {
            DQ.Real = -DQ.Real;
            DQ.Dual = -DQ.Dual;
        }
        // 3-2) Accumulate
        BlendedDQ.Real += DQ.Real * w;
        BlendedDQ.Dual += DQ.Dual * w;
    }
    TotalWeight += w;
}

// 4) Weight-normalize
BlendedDQ.Real *= (1.f / TotalWeight);
BlendedDQ.Dual *= (1.f / TotalWeight);

// 5) Final normalize
BlendedDQ.Normalize();