Abstract

뉴럴 네트워크의 정보 흡수 능력은 파라미터의 개수에 의해서 제한된다. Conditional computation은 모델의 연산량 대비 성능이 극적으로 향상할 수 있다고 제안된 이론이다. 하지만, 실제로는 알고리즘적으로 그리고 성능 한계가 존재한다. 본 논문에서는 conditional computation을 통해 아주 미세한 연산량 증가와 1000X 배의 성능 향상을 보였다.본 논문에서는 Sparsely-Gated Mixture-fo-Experts layer(MoE)를 제안한다. 학습 가능한 gating network는 각 샘플마다 어떻게 sparse combination을 사용할지 결정한다. 본 논문에서는 MoE를 language modeling 과 machine translation task에 적용하였다.

Introduction

1. Conditional computation

모델 용량을 증가시키기 위한 방법으로 conditional computation의 다양한 형태가 제안되었다. 네트워크의 큰 부분이 예제별로 활성화되거나 비활성화 되는 형태로 구성되며 gating decision은 binary 또는 희소하고 연속적일 수 있으며, 확률적이거나 deterministic할 수 있다. 게이트 결정을 학습하기 위해 다양한 형태의 강화학습과 역전파가 제안 되었다.

이러한 아이디어가 이론적으로 유망할지라도, 현재까지 모델 용량, 학습 시간 또는 모델 품질에서 엄청난 개선을 보여준 작업이 없었습니다. 이는 아래와 같은 이유 때문이라 하였습니다.

• 현대의 컴퓨팅 장치가 산술 연산에 비해 분기(branching)에서 더 느리다는 점.
• 큰 배치 크기가 성능에 중요한데, 조건부 연산이 이를 줄인다는 점.
• 네트워크 대역폭이 병목 현상이 될 수 있다는 점.
• 손실 항을 포함하여 원하는 희소성을 달성하기 위해 필요한 조정들.
• 매우 큰 데이터 세트를 다루는 모델 용량의 중요성.

여기서, 저자들은 위의 문제들을 모두 다루어 conditional computation의 효과성을 입증하였습니다.

2. Our approach: The Sparsely-Gated Mixture-of-Experts Layer

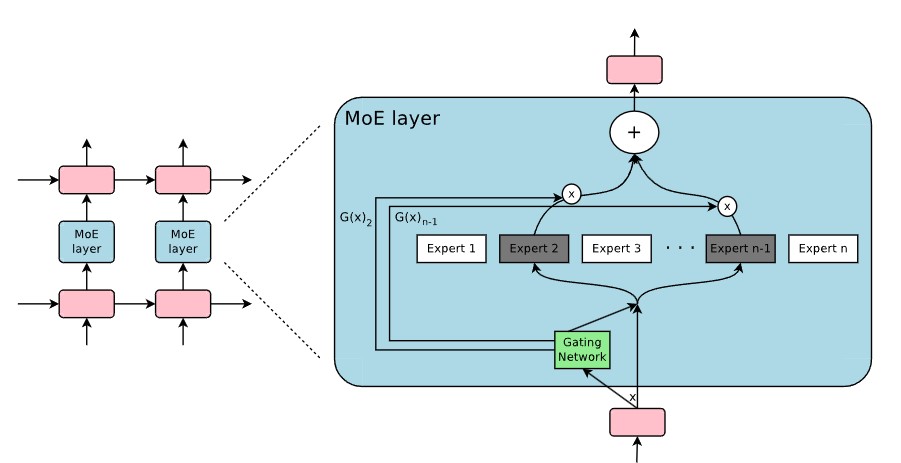
MoE는 여러 전문가들로 구성되며, 각각은 단순한 피드포워드 신경망입니다. 또한, 학습 가능한 게이팅 네트워크가 있어 각 입력을 처리하기 위해 전문가들의 희소한 조합을 선택합니다.

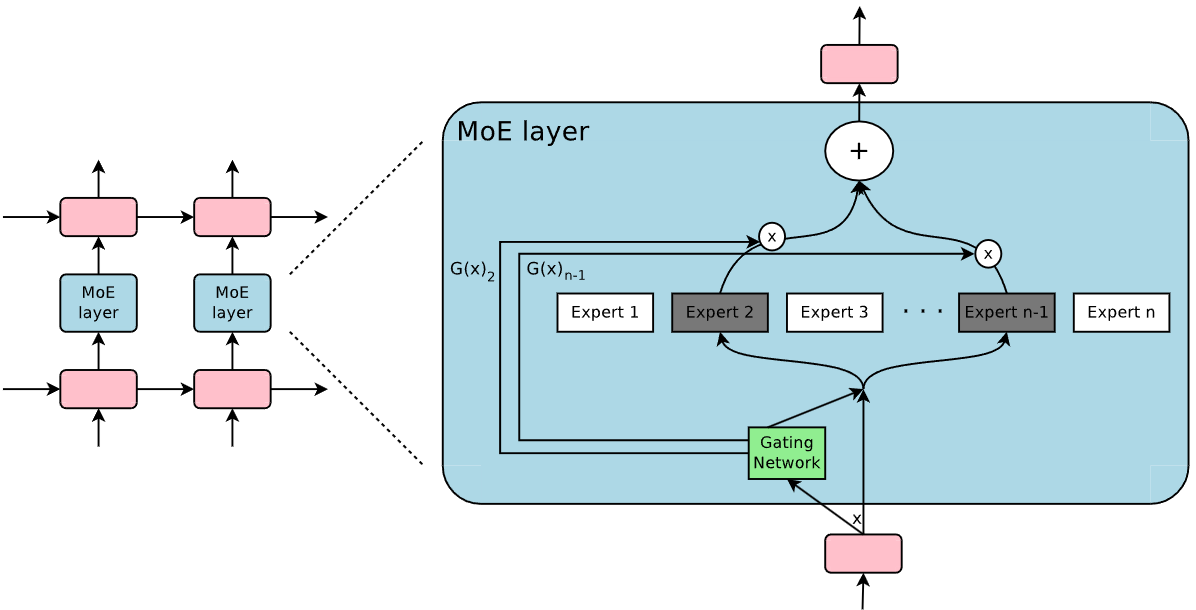
이 논문에서는 매우 큰 모델에서 이점을 얻는 것으로 알려진 언어 모델링 및 기계 번역 작업에 중점을 둡니다. 특히, 우리는 MoE를 쌓인 LSTM 레이어 사이에 컨볼루션 방식으로 적용합니다. 위 0그림처럼 MoE는 텍스트의 각 위치마다 한 번 호출되며, 각 위치에서 잠재적으로 다른 전문가 조합을 선택합니다. 다양한 전문가들은 구문 및 의미론에 따라 매우 전문화되는 경향이 있습니다.

The Structure of the Mixture-of-Experts Layer

연구 조건은 원칙적으로 전문가 네트워크들은 동일한 크기의 입력을 받아 동일한 크기의 출력을 생성해야 한다고 하지만, 이 논문에서는 동일한 구조를 가진 피드포워드 네트워크를 사용하지만, 각 네트워크는 서로 다른 매개변수를 가지는 조건으로 제약을 두었습니다.

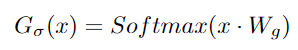
$G(x)$의 출력 희소성에 기반하여 계산을 절약합니다. $G(x)_i=0$인 경우, $E(x)$를 계산할 필요가 없습니다. 실험에서는 수천 명의 전문가를 보유하고 있지만, 각 예제에 대해 소수의 전문가만 평가하면 됩니다. 전문가의 수가 매우 많을 경우, 2단계 계층적 MoE를 사용하여 분기 요소를 줄일 수 있습니다. 계층적 MoE에서는 주 게이팅 네트워크가 각기 자체 게이팅 네트워크를 가진 2차 전문가 혼합체인 "전문가"의 희소 가중치 조합을 선택합니다. 다음에서는 일반적인 MoE에 중점을 둡니다. 계층적 MoE에 대한 자세한 내용은 부록 B에서 제공합니다.

1. Gating Network

Softmax Gating

Non-sparse gating function으로 가장 간단한 softmax gating 형태입니다.

Noisy Top-K Gating

Softmax gating network에 희소성과 노이즈를 추가합니다. Softmax 함수를 적용하기 전에 조정 가능한 가우시안 노이즈를 추가한 후 상위 k개의 값만 유지하고 나머지는 $-\infty$로 설정합니다. 위에서 설명한 바와 같이 희소성은 계산을 절약하는 데 도움이 됩니다. 이러한 형태의 희소성은 게이팅 함수 출력에서 이론적으로 무서운 불연속성을 만들 수 있지만, 실제로는 문제가 되지 않습니다. 각 구성 요소의 노이즈 양은 두 번째 학습 가능한 가중치 행렬 $W_{noise}$에 의해 제어됩니다.

Softplus 함수는 ReLU 함수의 부드러운 근사치로 정의됩니다.
StandardNOrmal 함수는 평균이 0이고 표준편차가 1인 표준 정규 분포를 나타냅니다.

Training the Gating Network

모델의 나머지 부분과 함께 단순 역전파를 통해 게이팅 네트워크를 훈련합니다. $k>1$을 선택하면 상위 k 전문가의 게이트 값은 게이팅 네트워크의 가중치에 대해 0이 아닌 도함수를 가집니다.

Addressing Performance Challenges

1. The Shrinking batch problem

현대의 CPU와 GPU에서는 계산 효율성을 위해 큰 배치 크기가 필요합니다. 이는 매개변수 로드와 업데이트의 오버헤드를 분산시키기 위함입니다. 게이팅 네트워크가 각 예제에 대해 n명의 전문가 중 k명을 선택하면, b개의 예제로 구성된 배치에서 각 전문가는 대략 $\frac {kb}n$
개의 예제를 받게 됩니다. 이는 전문가 수가 증가할수록 단순한 MoE(혼합 전문가) 구현이 매우 비효율적으로 되는 원인이 됩니다. 이 축소된 배치 문제의 해결책은 원래 배치 크기를 가능한 한 크게 만드는 것입니다. 그러나 배치 크기는 전방 및 후방 패스 사이의 활성화를 저장하는 데 필요한 메모리에 의해 제한되는 경향이 있습니다. 우리는 배치 크기를 늘리기 위한 다음과 같은 기술을 제안합니다.

Mixing Data Parallelism and Model Parallelism

(아직 잘 이해하지 못함.)

Network Bandwidth

입출력 차원보다 expert의 hidden size가 더 커야한다는 의미입니다.

Balancing Expert Utilization

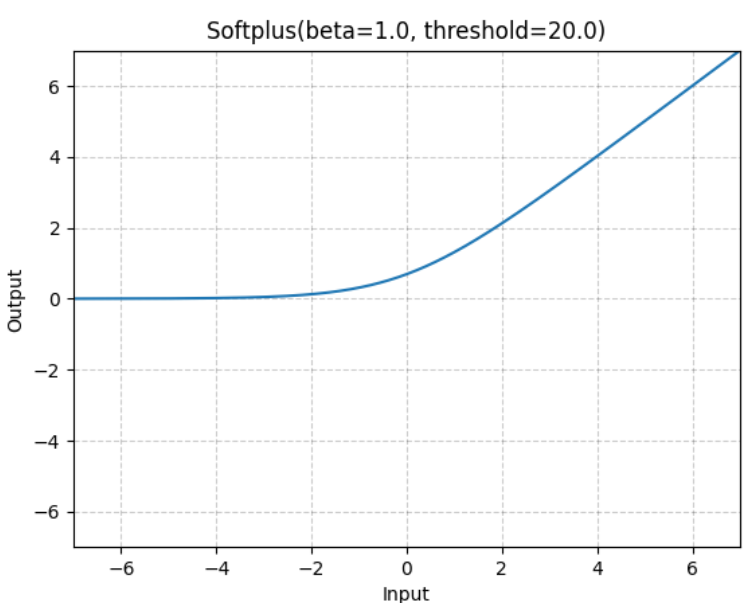
게이팅 네트워크가 항상 동일한 몇몇 전문가들에게 큰 가중치를 부여하는 상태로 수렴하는 경향이 있음을 관찰했습니다. 이 불균형은 self-reinforcing하며, 선호되는 전문가들이 더 빠르게 훈련되어 게이팅 네트워크에 의해 더욱 많이 선택되기 때문입니다.

이 논문은 soft constraint 접근법을 취합니다. 전문가의 중요성을 훈련 예제 배치에 대해 해당 전문가의 게이트 값의 배치 합으로 정의합니다.

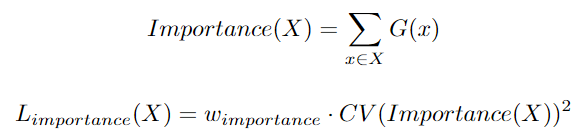
여기서 $X$는 배치이고, $w_{importance}$는 스케일링 인자, $CV$는 coefficient of Variation입니다.

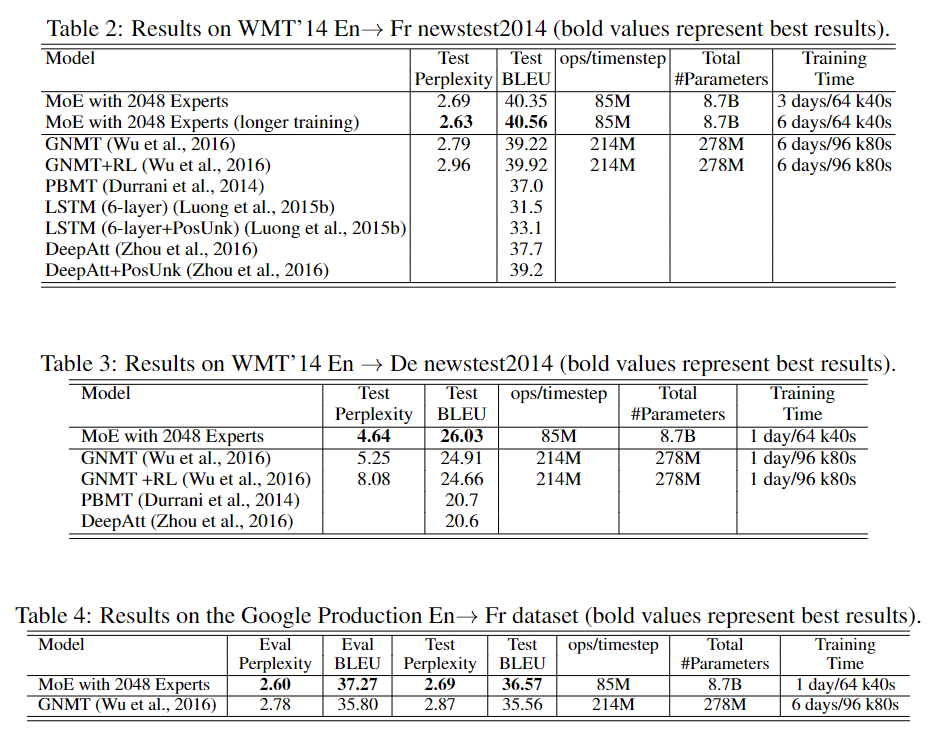
Experiments

Low computation, Varied capacity

낮은 computation과 높은 성능 향상을 보였습니다.

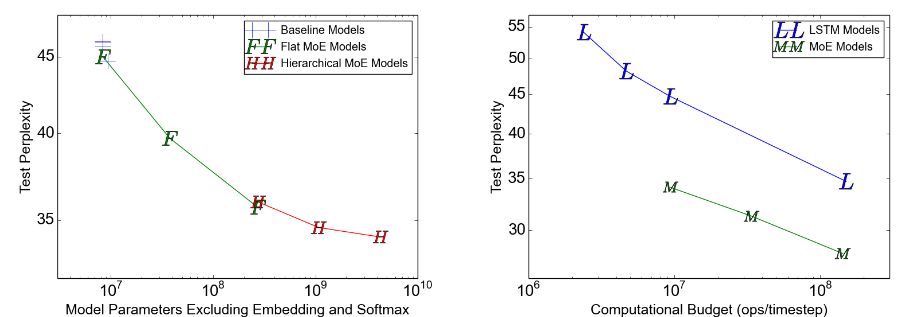
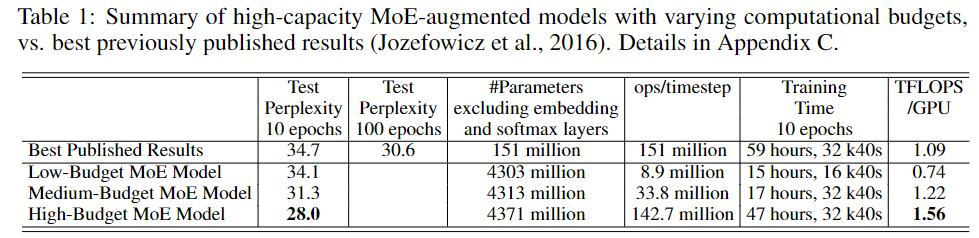
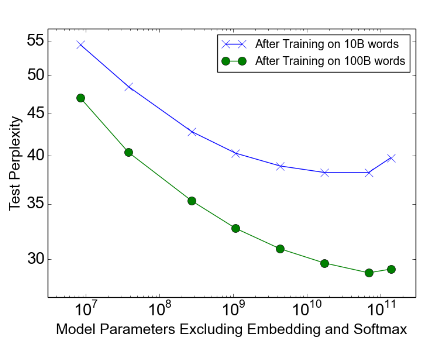
100Billion word google news corpus

훈련데이터를 많이 학습시키고 나서 성능 향상을 보입니다.