Point Transformer

1. Background

본 논문에서는 기존의 self-attention 방식은 모든 point에 대해서 한번에 global features를 뽑기 때문에 large-scale 3D scene understanding에서는 적용할 수 없다는 점을 지적하였습니다. 그렇다면 기존의 방법과 어떠한 차이가 있는지 살펴보겠습니다.

• Standard scalar dot-product attention layer

  Let$\space\mathcal{X} = \{x_i\}_i$ 가 feature vectors의 집합이라고 할때, 아래의 수식으로 나타내어집니다.

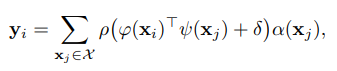
$y_i$는 output feature입니다.$\phi, \psi, \alpha$는 pointwise feature transformation이고 주로 linear projections이나 MLPs가 사용됩니다. $\delta$는 position encoding 함수이고 $\rho$는 normalization 함수이며 주로 softmax 함수를 사용합니다. 그렇다면 vector attention은 무엇일까요?
$\space$
(정보)
위의 수식에 $\mathcal{X}$ 는 calligraphic X 라고 하여 보통 특정한 종류의 집합을 나타내기 위해 사용합니다. 이는 특별한 성질을 가진 집합이거나, 수학적 구조의 집합을 의미한다고 합니다. 일반적인 $X$는 일반적으로 변수의 개념이지만, $\mathcal{X}$는 집합에서 많이 쓰입니다.)

---

• Vector attention

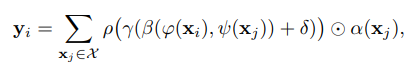
어떤 차이점이 보이시나요? $\beta$ 함수가 눈에 띕니다. 이 함수는 relation function으로 예로, subtraction 함수 등이 있습니다. 그리고 $\gamma$ 함수를 통해 feature aggregation을 위한 attention vectors로 projection 합니다.
$\space$
standard scalar dot-product attention에서는 이름에서 알 수 있듯 scalar값이 attention 값으로 계산됩니다. 하지만 vector attention에서는 vector값으로 attention 값이 연산되어 각 채널마다 서로 다른 att weights를 줄 수 있다는 이점이 있습니다.

2. Point Transformer Layer

본 논문에서 제안한 방법 중 가장 중요한 부분입니다. 자연스럽게 self-attention은 불규칙적으로 metric space에 임베딩 되어 있는 point clouds의 특성을 잘 반영해줄 수 있다고 했습니다. point transformer layer는 vector self-attention을 적용하였고 subtraction relation 과 position encoding $\delta$ 를 attention vecotr $\gamma$ 와 transformed features $\alpha$ 동일하게 적용합니다.
중요한 부분은 $\mathcal{X}$ 에서 kNN을 통해 local neighborhood subset $\mathcal{X(i)}$ 을 구합니다. 이렇게 찾은 이웃 점들에 대해서 position encoding은 각 points의 좌표 차이를 비선형 변환을 거쳐 더해주게 됩니다.

전체 points에 대해서 수행하는 것이 아닌 kNN을 통해 추출된 subset에 대해서 이러한 attention과 position encoding을 적용함으로써 locally(지역적)으로 적용했다고 볼 수 있습니다.

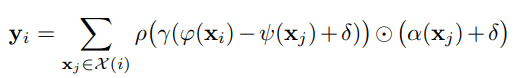
조금 있다가 다루겠지만, 본 논문에서 position encoding은 sine, cosine 주기를 더해주는 것이 아니라 adaptive하게 위치를 지정하도록 뉴럴 넷으로 학습합니다. 따라서 ene-to-end로 모델이 스스로 위치까지 지정해주는 효과를 가질 수 있습니다. point transformer layer의 구조는 아래 그림과 같습니다.

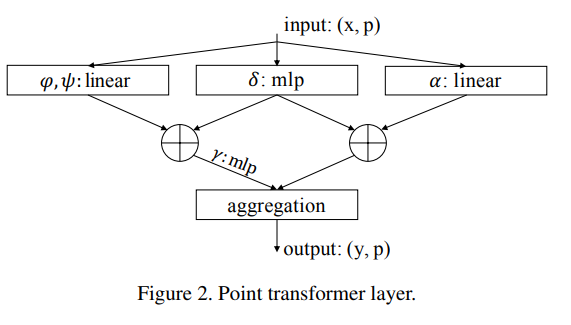
3. Position Encoding

slef-attention 에서 position encoding은 operator가 데이터의 local structure에 적응(adapt)할 수 있도록 하는 중요한 역할을 합니다. 기존의 position encoding은 sine, cosine 함수 또는 normalized range value를 더해주었습니다. 3D point cloud processing에서는 3D point 좌표 그 자체로 position encoding의 후보자(candidate)라고 합니다. 따라서, 학습가능한 파라미터화된 position encoding을 제안하였습니다.

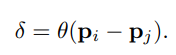
$P_i, P_j$는 각 3D point 좌표들이고 $\theta$는 2개의 linear layer + 1개의 ReLU를 포함한 MLP 입니다.
(어떻게 포인트를 선정하는 것인지 아직 이해되지 않아 더 읽어보겠습니다...)

4. Point Transformer Block

point transformer에 self-attention이 포함되어 있습니다. linear projection을 통해 차원 축소와 연산 가속을 할 수 있고 이는 residual connection으로 최종 출력에 전달됩니다. 입력값은 feature vectors x와 3D 좌표값 p가 주어집니다.

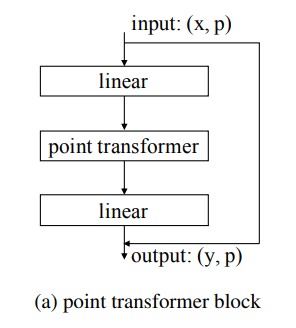
point transform 과정은 지역화된 특징 벡터들 간의 정보 교환을 촉진하고, 모든 데이터 포인트에 대한 새로운 특징 벡터들을 출력으로 생성하도록 하여 특징 벡터의 information 뿐만 아니라 3차원 공간에서의 배치에도 적응합니다.

5. Network Architecture

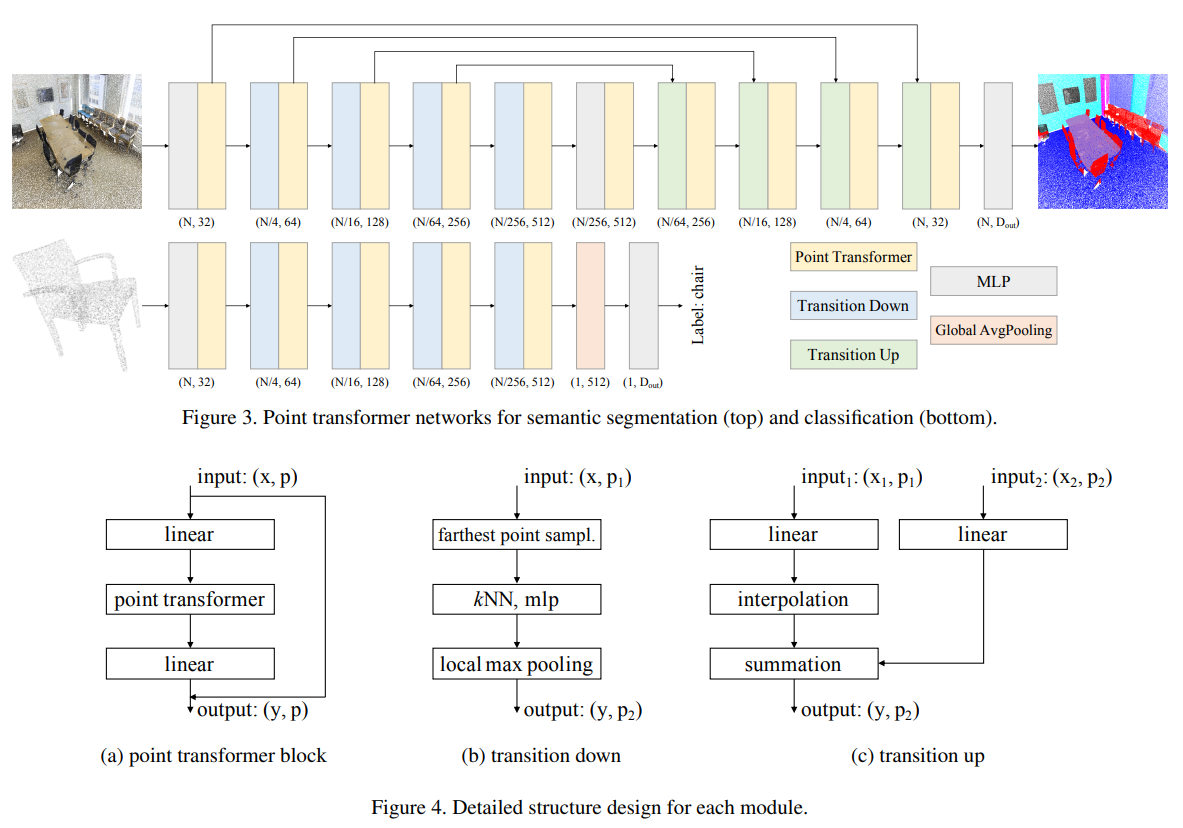
네트워크 구조의 큰 특징은 convolution 연산과 auxiliary branches가 없다는 점입니다. 오직 main branch로 point tranformer layers, pointwise transformation, 그리고 pooling만 사용합니다.

각 block을 차례대로 살펴보겠습니다.

• Backbone structure

  point transformer 네트워크에서 feature encoder는 semantic segmentation과 classification에서 순차적으로 5 단계로 구성된 downsampled point sets을 거칩니다. downsampling rates는 각 단계별로 [1, 4, 4 ,4 ,4] 이며 point set의 카디널리티는 각 단계별로 [N, N/4, N/16, N/64, N/256] (N은 input points의 수)이 됩니다. downsampling rates는 목적에 따라 바뀔 수 있습니다.

• Transition down

  downsampling을 할때 입력값이 x와 p가 있었습니다. 각 데이터 특성에 맞춰 downsampling을 수행해줍니다. 먼저 point p에 대해서는 farthest point sampling(FPS) 방식을 사용하여 필수적인 카디널리티(점의 개수) 만큼 추출합니다. 그리고 입력값 x에 대해서는 선별된 point p를 기준으로 kNN(k=16)을 통해 이웃점들의 값의 최대값으로 local max pooling해줍니다. 아래의 그림으로 구조를 보겠습니다.
  

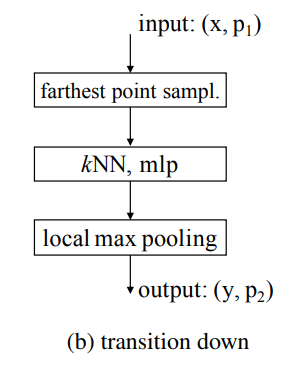
• Transition up

  semantic segmentation에서는 U-net 구조를 가져왔습니다. 이는 인코더와 디코더가 대칭으로 짝을 이루는 구조입니다. 인코딩을 통해 downsampling 되었기에 skip connection을 통해 더해주려면 interpolate 과정을 거쳐야합니다. 본 논문에서는 trilinear interpolation을 통해 보간합니다. 아래의 구조에서 linear는 linear layer + BN + ReLU를 묶어서 표현한 것 입니다.
  

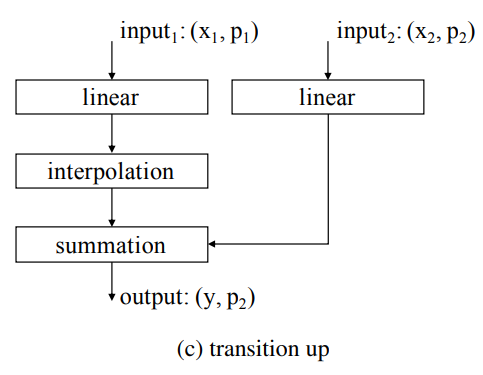
• Output head

  Semantic segmentation에서는 MLP를 통해 마지막 mapping을 거쳐 logits을 얻습니다. Classification에서는 전체 point set에서 global feature vector를 뽑기 위해 global average pooling을 수행한 뒤, MLP를 통해 global classification logits을 얻습니다.

Experiments로 넘어가기전에 앞에서 자세히 언급되지 않은 알고리즘에 대해 이해해보겠습니다.

---

조금 더 살펴봐야할 점은 downsampling을 위한 FPS 방식과 upsampling을 위한 trilinear interplotation 방식입니다. 해당 알고리즘을 이해해보겠습니다.

Farthest Point Sampling(FPS)

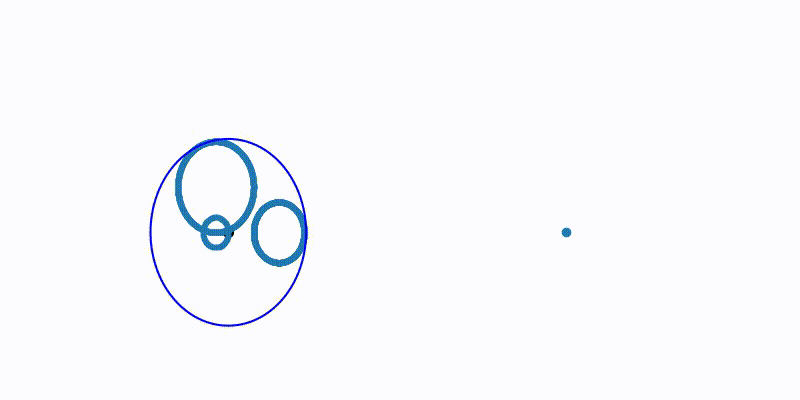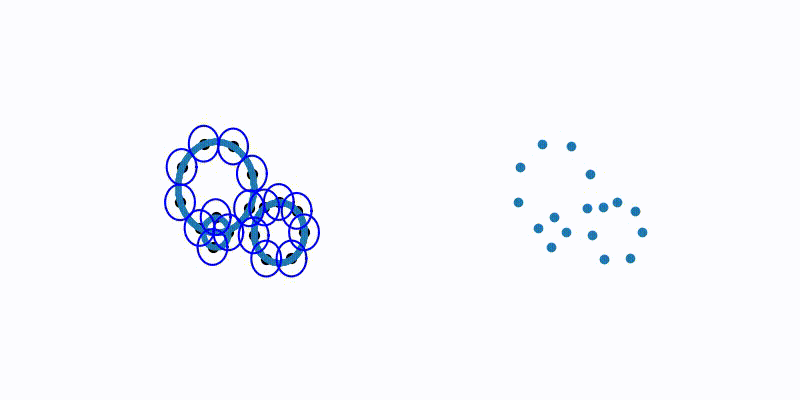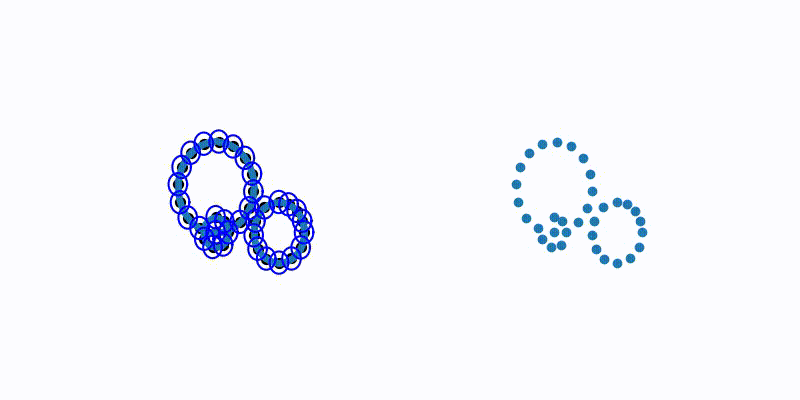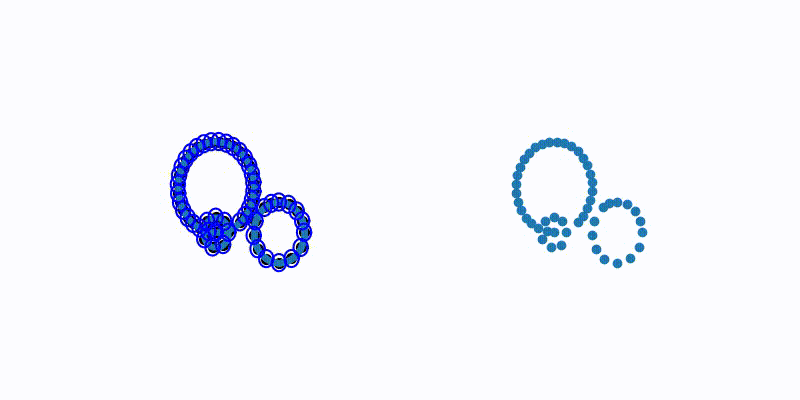
PointNet++ 논문에서 사용된 방법입니다. 임의의 point를 선택하고 해당 point와 가장 거리가 먼 point를 선택합니다. 이렇게 선택된 point를 기준으로 다음으로 거리가 가장 먼 point를 찾고자 하는 point 개수 K개를 뽑을 때까지 반복합니다. 아래의 그림과 코드을 통해 이해해봅시다.
FPS 참고문헌

def getGreedyPerm(D):
    """
    A Naive O(N^2) algorithm to do furthest points sampling
    
    Parameters
    ----------
    D : ndarray (N, N) 
        An NxN distance matrix for points
    Return
    ------
    tuple (list, list) 
        (permutation (N-length array of indices), 
        lambdas (N-length array of insertion radii))
    """
    
    N = D.shape[0]
    #By default, takes the first point in the list to be the
    #first point in the permutation, but could be random
    perm = np.zeros(N, dtype=np.int64)
    lambdas = np.zeros(N)
    ds = D[0, :]
    for i in range(1, N):
        idx = np.argmax(ds)
        perm[i] = idx
        lambdas[i] = ds[idx]
        ds = np.minimum(ds, D[idx, :])
    return (perm, lambdas)

Trilinear interpolation

점을 보간할 때 가장 쉬운 방법은 가까운 점에 맞추어서 그 점의 특성으로 채우는 것입니다. 하지만, 그렇게 하면 컴퓨팅 연산의 소요량과 매번 가까운 점을 계산해야하기에 비효율적입니다. 이에 대한 예시로 아래의 그림을 봅시다.

앞선 방법과 달리 이번에는 trilinear interpoltation 방식을 살펴보겠습니다. tri가 붙은 이유는 linear interpolation이 3번 사용되기 때문입니다. linear interpolation에 대해 아래 그림으로 이해할 수 있습니다.

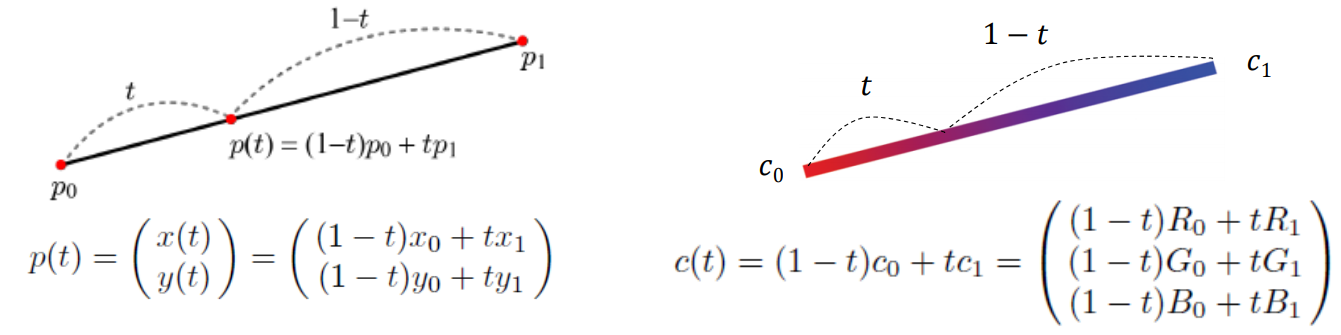
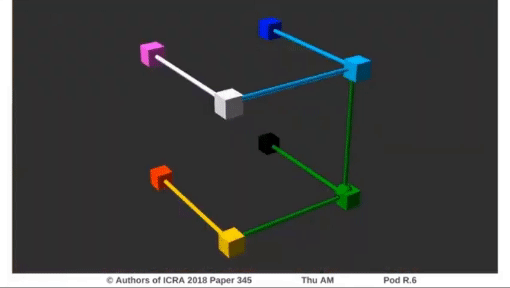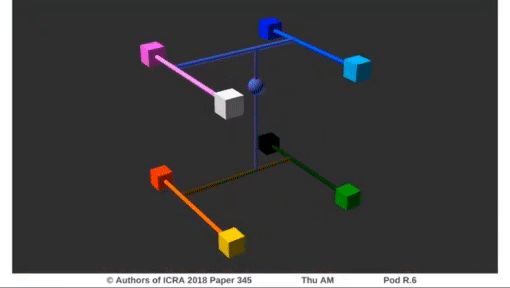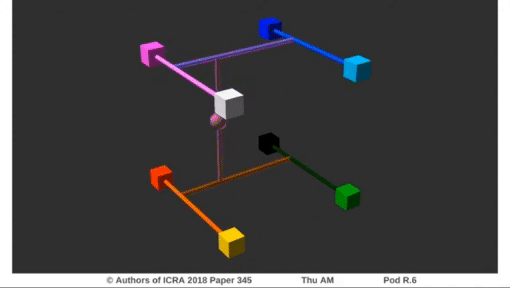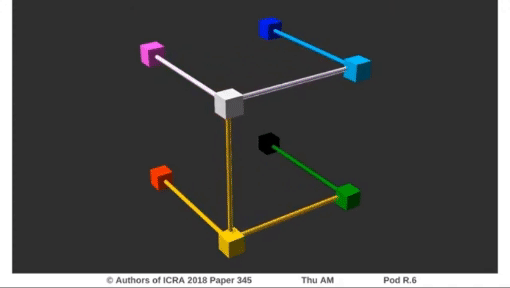
그렇다면 이러한 보간이 3번 이루어진다는 뜻은 먼저 두 선분에 대해서 보간을 한 뒤에 그 두 선분 사이를 다시 선형 보간함을 뜻합니다. 아래의 그림으로 이해할 수 있습니다.

---

Experiments

실험은 크게 semantic segmentation, 3D shape classification, object part segmentation task에 대해 수행하였습니다.

1. Semantic segmentation

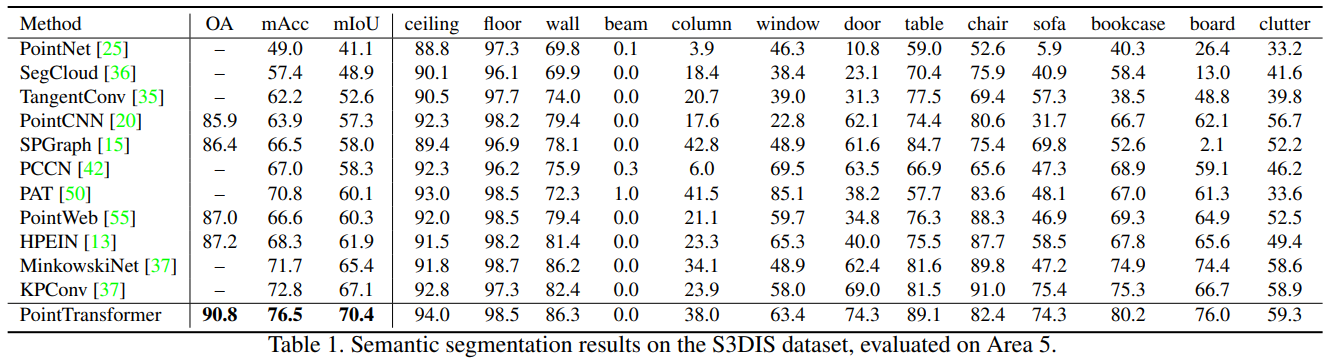MLP기반의 PointNet, Voxel기반의 SegCloud, graph기반의 SPGraph, attention기반의 PAT, sparse convolutional networks 기반의 KPConv 등과 비교 실험을 하였습니다. 비교 실험 결과 평가 지표, mean classwise intersection over union (mIoU), mean of classwise accuracy (mAcc), overall pointwise accuracy (OA)에 대해서 모두 아주 뛰어난 성능을 보였습니다. 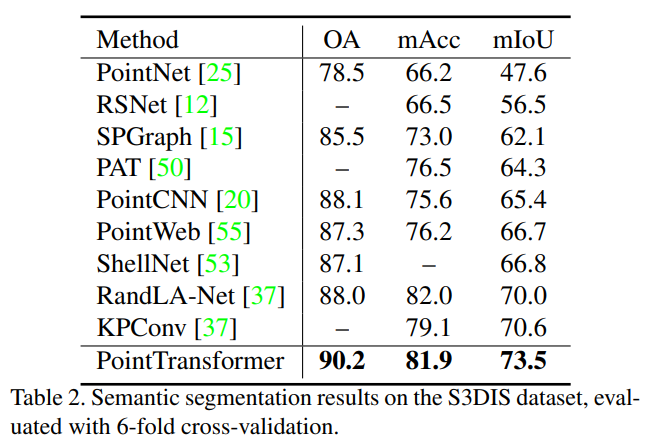그리고 6-fold cross-validation에 대한 실험도 추가하였습니다. cross-validation에 대한 실험 결과를 보여주는 논문은 드물었던 것 같은데 cross-validation을 통한 실험 결과를 보임으로써 확실하게 모든 면에서 우수하다는 것을 증명하였습니다.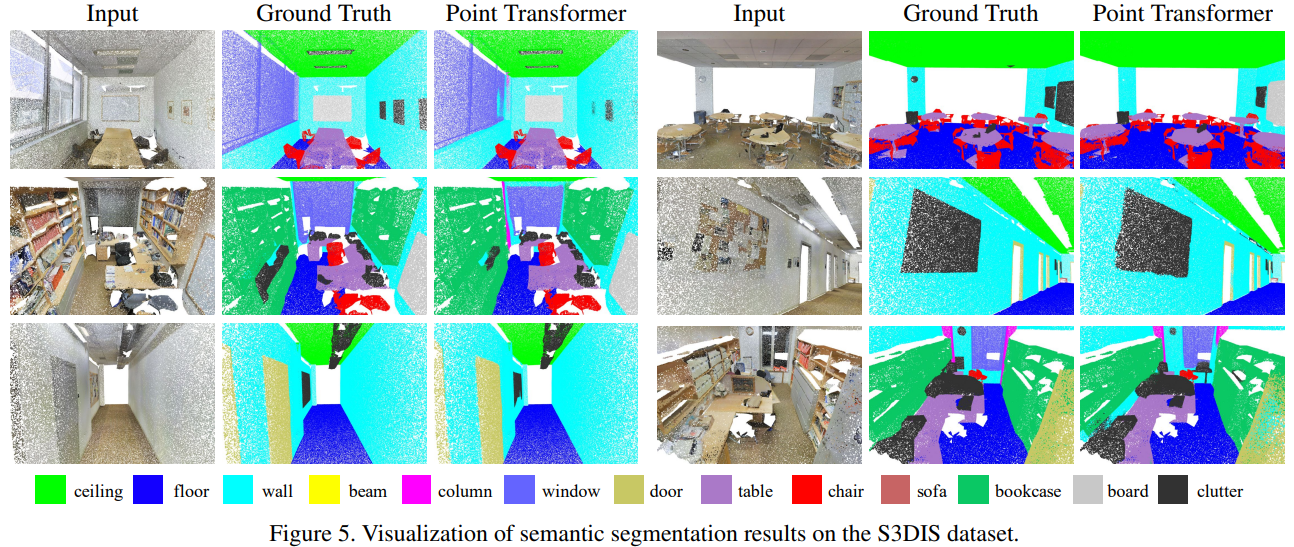실제 semantic segmentation 결과를 보면 정답값 Ground Truth와 아주 비슷하게 잘 예측하는 것을 확인할 수 있습니다.(역시 CVPR...)

2. Shape Classification

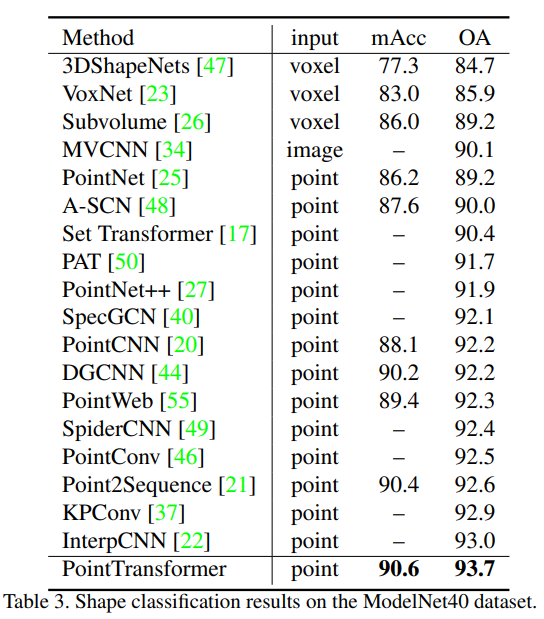
Classification 결과 또한 가장 우수한 결과를 확인할 수 있습니다.
저는 Fig6에서 보인 그림 자료가 흥미로웠습니다.

output feature에 대해 최근접 이웃을 뽑아 시각화 해본 그림입니다. 확실히 가까운 이웃에는 전체적인 shape은 유사하지만, 차이가 나는 부분은 우리가 의미적으로 덜 중요하다고 인식하는 부분에서 보입니다. 그리고 retrieval이라고 한 이유는 output feature와 가장 유사한 벡터를 뽑음으로서 질문을 통해 벡터를 뽑았기 때문입니다. (딥러닝 참 대단하네요. 이러한 shape을 수치적으로 비슷한 곳에 놓이도록 학습하다니)

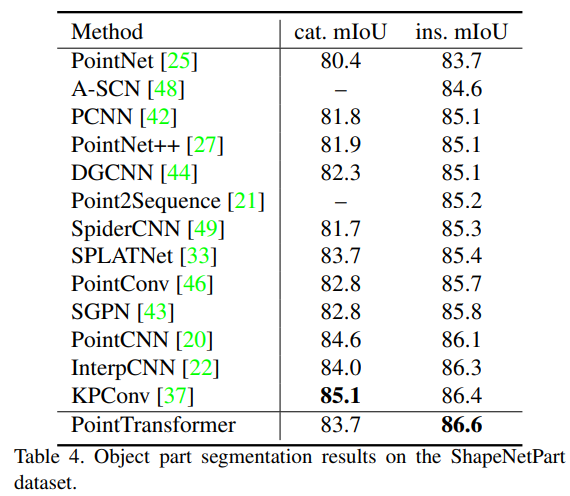
3. Object Part Segmentation

Abliation Study

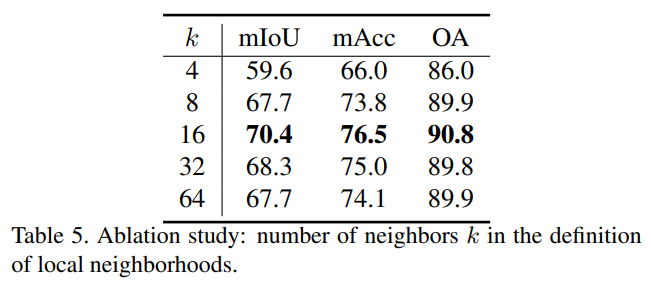
1. Number of neighbors

neighbors k의 개수에 따른 실험입니다. 각 point에 대한 local 이웃을 얼마나 정할까에 대한 의문이 풀어지는 실험입니다. 가장 좋은 성능은 k=16일때입니다. 만약 k가 4, 8보다 작다면 모델은 예측하기에 부족한 문맥 정보를 가집니다. 또 k가 32, 64 보다 크다면 관련성이 작은 점들까지 포함됨을 알 수 있습니다. 이는 너무 많은 노이즈를 주기 때문에 모델의 성능이 떨어지는 것 같습니다.

2. Softmax regularization

softmax 적용 전 (66.5%/72.8%/89.3%) -> softmax 적용 후(70.4%/76.5%90.8%). softmax function은 취할 때가 취하지 않았을 때보다 월등하게 좋습니다.

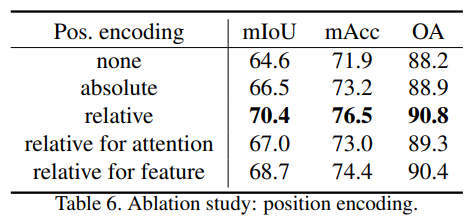
3. Position encoding

position encoding을 적용하지 않았을때, 절대값으로 적용하였을 때, attention generation branch, feature transformation branch 모두 적용하였을 때, 각각 만 적용하였을 때로 실험하였습니다.

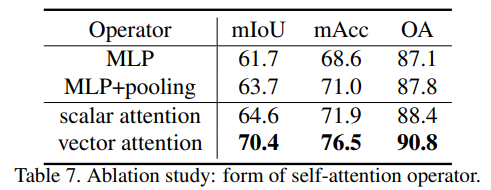
4. Attention type

Attention type은 attention을 적용하지 않은 MLP, MLP+pooling보다 attention을 적용하였을 때 높게 나옵니다. 그리고 point cloud의 특성을 반영한 vector attention을 통해 월등히 좋은 성능을 보입니다. scalar attention은 모든 vector에 대해 동일한 attention wegihts을 부여하는것과 달리 vector attention은 각 채널별로 attention 가중치를 부여하기에 더 문맥적으로 잘 파악한 것이라 해석됩니다.

Conclusion

포인트 클라우드 처리에 있어 트랜스포머는 언어나 이미지 처리보다 더 자연스러운 적합성을 보입니다. 이는 포인트 클라우드가 본질적으로 메트릭 공간에 내장된 집합이며, self-attention 연산자가 근본적으로 집합 연산자이기 때문입니다. 이러한 개념적 호환성을 넘어, 트랜스포머가 포인트 클라우드 처리에서 매우 효과적임을 보여주며, 다양한 모델을 뛰어넘는 성능을 보입니다.

Opinion

모델 설계에 있어서 어떤 식으로 파라미터를 주었는지, 어떻게 layer를 쌓았는지 의문이 드는 부분이 많았지만 광범위한 실험과 abliation study를 통해 해소되었습니다. 그렇기에 논문의 내용이 더욱 완결성있고 깔끔했던 것 같습니다. 배울 점이 많이 보이는 좋은 논문입니다!

다만, point를 sampling하는 방식 그리고 다음에 review할 point-MAE 논문처럼 해당 모델의 구조를 통해 적용될 수 있는 방법이 매우 많습니다. 이러한 부분들을 추가적으로 적용해보며 또 좋은 논문을 쓸 수 있을거 같습니다.

1. Zhao, Hengshuang, et al. "Point transformer." Proceedings of the IEEE/CVF international conference on computer vision. 2021.
2. Qi, Charles Ruizhongtai, et al. "Pointnet++: Deep hierarchical feature learning on point sets in a metric space." Advances in neural information processing systems 30 (2017).