1. RANSAC의 필요성

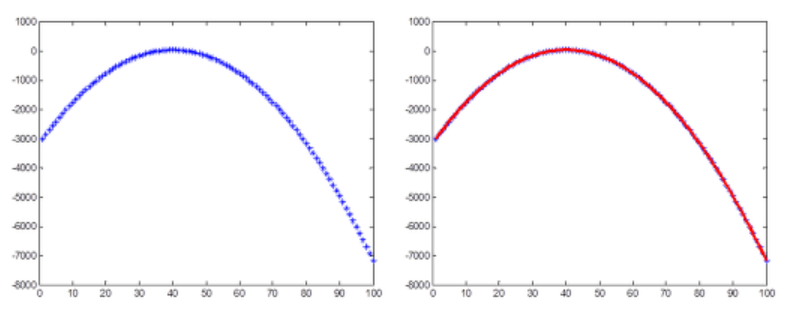
RANSAC이 왜 필요한지 살펴보자. 아래 왼쪽 그림과 같이 관측된 데이터들이 있다고 하자. 이 데이터들을 최소자승법을 이용하여 포물선으로 근사(fitting)시키면 오른쪽 그림과 같은 결과가 나온다. 참고로, 최소자승법이란 모델(여기서는 포물선)과의 ∑residual2을 최소화하도록 모델 파라미터를 정하는 방법을 말한다.

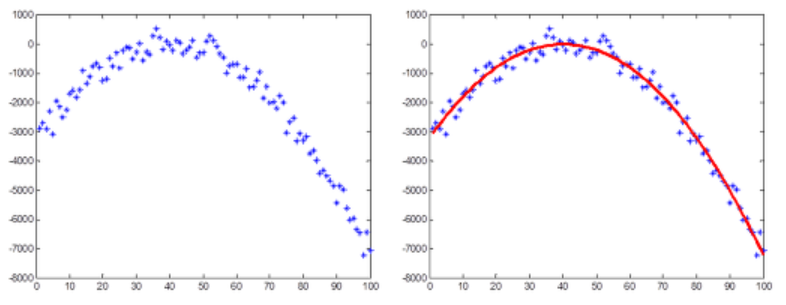
그런데, 실제 관측 데이터가 위와 같이 깨끗하게 나오는 경우는 현실 세계에서는 별로 없다. 측정 오차나 노이즈 등으로 인해 아래 왼쪽 그림 같은 경우가 일반적일 것이다. 이때도 최소자승법을 적용하면 오른쪽 그림과 같이 휼륭한 결과를 얻을 수 있다.
,

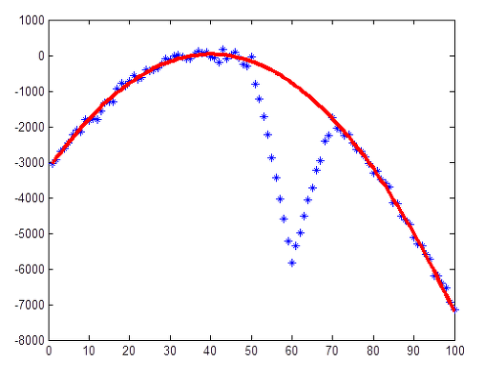
그런데, 만일 아래 왼쪽 그림과 같이 약간의 노이즈 정도가 아니라 데이터 자체가 완전히 틀어져 버린 경우는 어떻게 될까? 이렇게 정상적인 분포에서 벗어난, 이상한 데이터들을 이상점(outlier)라고 부르는데, 데이터에 outlier(아웃라이어)가 끼어 있으면 최소자승법은 오른쪽 그림처럼 엉망이 되어 버린다.

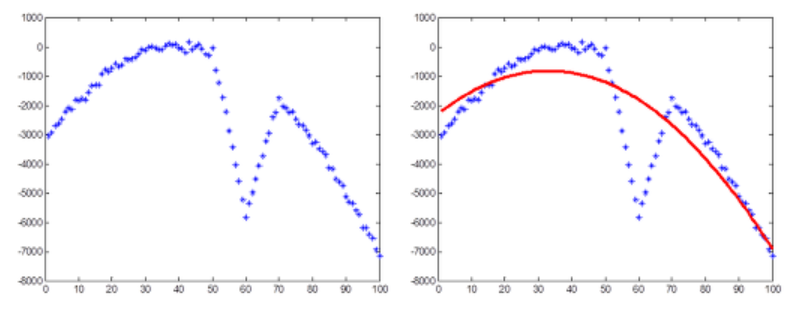
그런데, 이것을 RANSAC을 이용해 근사시키면 아래 그림과 같이 깨끗한 결과를 얻을 수 있다.

2. RANSAC의 이해

RANSAC은 RANdom SAmple consensus의 약자로, 데이터셋에서 노이즈를 제거하고 모델의 예측하는 알고리즘이다.

RANSAC은 특정 임계값 이상의 데이터를 완전히 무시해버리는 특성이 있어 outlier에 강건한 알고리즘이다.

최소자승법(least square method)는 데이터들과의 잔차의 SS(Sum of Squares)를 최소화하도록 모델을 찾지만 RANSAC은 컨센서스가 최대인, 즉 가장 많은 수의 데이터들로부터 지지를 받는 모델을 선택하는 방법이다.

3. RANSAC 알고리즘

1. 원본 데이터에서 무작위로 부분 집합을 선택합니다. 이 부분 집합을 hypothetical inliers라고 부른다.
2. hypothetical inliers 집합에 모델을 fit한다.
3. 그 다음 모든 데이터를 적합된 모델에 대해 테스트한다. 모델 특정 손실 함수에 따라 예상 모델에 잘 맞는 원본 데이터의 모든 데이터 포인트들을 consensus set(즉, 모델의 inliers 집합)라고 부른다.
4. 충분히 많은 데이터 포인트가 consensus set의 일부로 분류되었다면 추정된 모델은 합리적으로 좋은 것으로 간주된다.
5. 모델은 consensus set의 모든 멤버를 사용하여 재추정함으로써 개선될 수 있다. 이후 반복에서 이 측정치를 적합성 품질 기준으로 설정함으로써, 모델 적합을 개선하기 위해 적합성 품질을 측정 기준으로 사용한다.

충분히 좋은 모델 parameter set으로 학습하기 위해서는, 위의 절차는 고정된 횟수로 매 수행마다 좋은 모델로 갱신되도록 학습되어야한다.

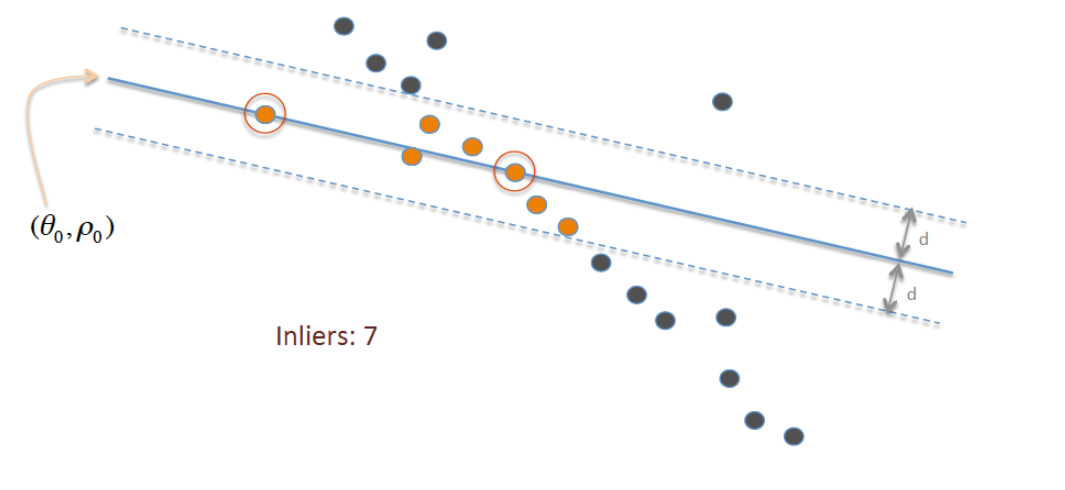
7개의 inliers를 포함하도록 학습된 linear 모델이다. 이는 대부분의 data points의 분포를 반영하지 못하기에 잘 학습되지 못한 예이다.

4. pseudocode

Given:
    data – A set of observations.
    model – A model to explain the observed data points.
    n – The minimum number of data points required to estimate the model parameters.
    k – The maximum number of iterations allowed in the algorithm.
    t – A threshold value to determine data points that are fit well by the model (inlier).
    d – The number of close data points (inliers) required to assert that the model fits well to the data.

Return:
    bestFit – The model parameters which may best fit the data (or null if no good model is found).


iterations = 0
bestFit = null
bestErr = something really large // This parameter is used to sharpen the model parameters to the best data fitting as iterations go on.

while iterations < k do
    maybeInliers := n randomly selected values from data
    maybeModel := model parameters fitted to maybeInliers
    confirmedInliers := empty set
    for every point in data do
        if point fits maybeModel with an error smaller than t then
             add point to confirmedInliers
        end if
    end for
    if the number of elements in confirmedInliers is > d then
        // This implies that we may have found a good model.
        // Now test how good it is.
        betterModel := model parameters fitted to all the points in confirmedInliers
        thisErr := a measure of how well betterModel fits these points
        if thisErr < bestErr then
            bestFit := betterModel
            bestErr := thisErr
        end if
    end if
    increment iterations
end while

return bestFit

5. Parameters

RANSAC에서는 크게 2가지 파라미터를 결정해야한다. 몇 번($k$) 반복할 것인지, inlier로 볼 threshold 값($t$)는 어떻게 정할지 결정해야한다.
요구하는 성공 확률($p$)에 따라서 결정될 수 있다. $w$는 매 step마다 inlier를 선택할 확률이다.

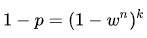
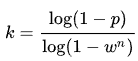
6. RANSAC과 robust 파라미터 추정

사실 RANSAC은 robust parameter estimation 방법들 중 하나이다. 어떤 방법 또는 알고리즘이 데이터 중에 outlier가 있어도 처리가 가능하면 이를 robust하다 라고 한다.

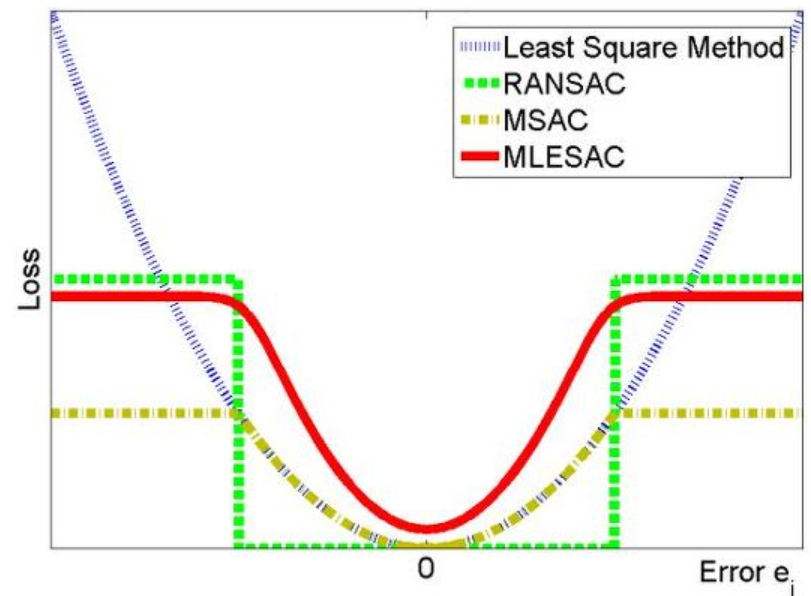
Robust한 파라미터 추정(estimation) 방법으로는 RANSAC 외에도, M-estimator, LMedS 등이 있다. 이러한 robust 파라미터 추정 방법들은 Loss 함수에 따라 구분지을 수 있는데, 일단 아래 그림을 살펴보자.