이 포스트는 윤형석님의 Point Cloud Features 발표를 듣고, 공식 포스트를 참고하여 작성하였습니다.

참고한 유튜브

• AIRLAB@KHU 논문세미나

Feature Descriptors 필요성

Feature Descriptors

타입에 따라 크게 Global과 local로 나뉜다.

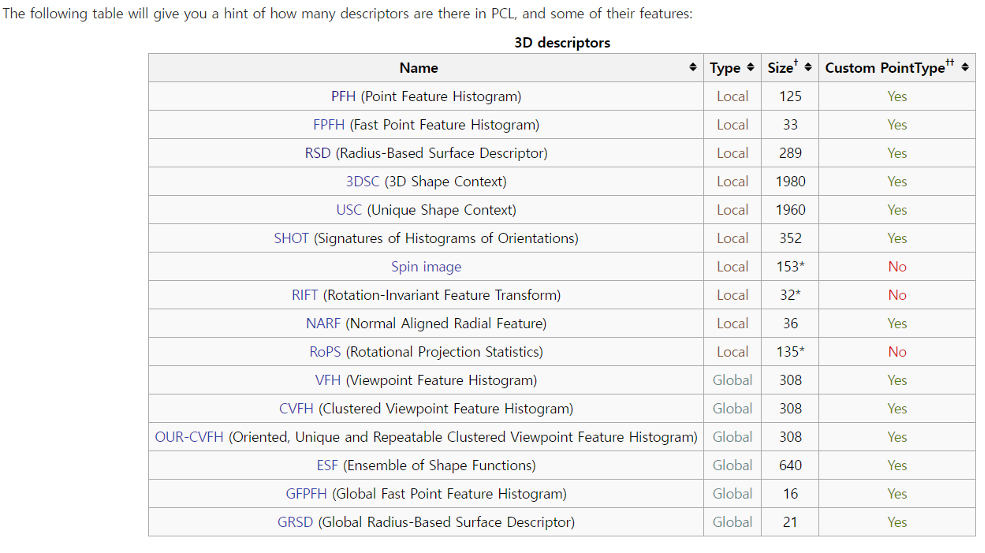
point cloud feature descriptors는 방법에 따라 크게 histogram-based와 signature-based로 나뉜다.

Point Feature Histograms(PFH)의 필요성

surface normals와 curvature estimates는 특정한 점 주변을 나타내는 geometry의 기본적인 representation이다. 비록, 아주 빠르고 계산하기 쉽지만, 오직 few values의 point's k-neighborhood로 geometry를 근사하기 때문에 detail하게 포착할 수 없다. 결국, 대부분의 points는 같거나 아주 유사한 feature values를 지닐 것이고 그럼으로 informative characteristics를 감소시킨다.

PFH(Point Feature HIstograms)의 이론적 이점과 PCL 관점에서 구현 디테일을 살펴보고자한다. PFH는 xyz 3D data와 surface normals에 의존하기에 Estimating Surface Normals in a Point Cloud 포스트를 보고 오길 권장한다.

PFH 이론

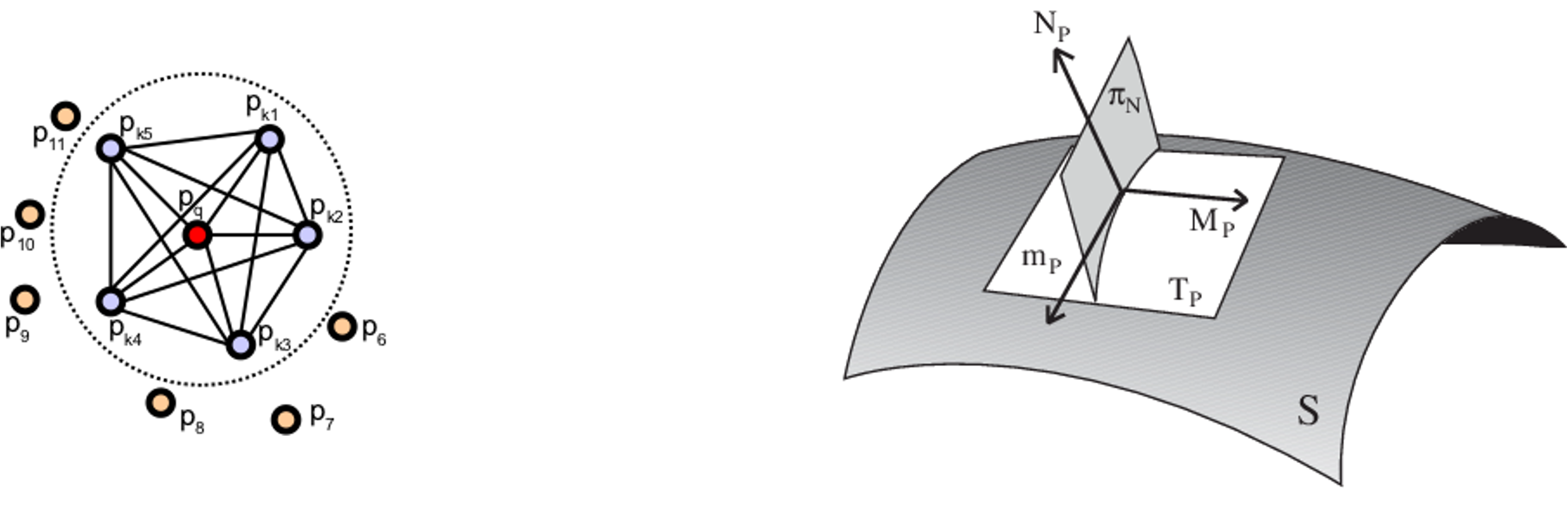
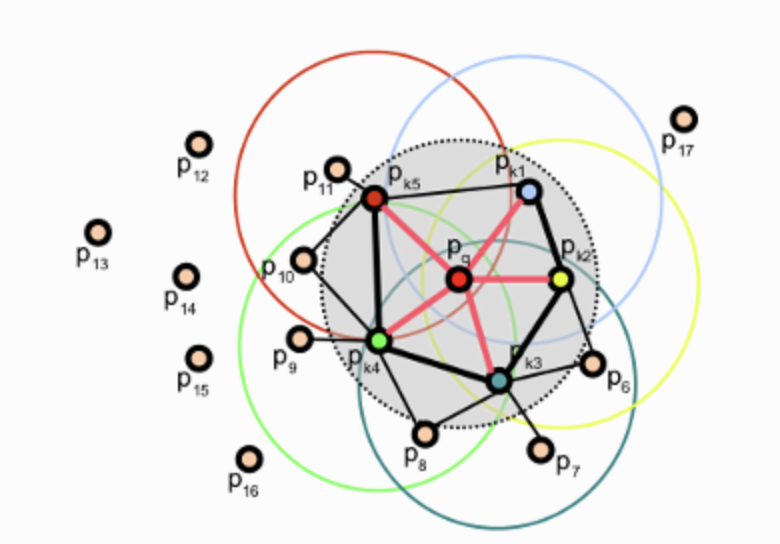
1. 임의의 한 점을 선택하고 반지름이 r인 구안에 속한 neighbor points를 선택한다. (K-neighborhood)
2. 모든 점들의 쌍 $p_s$와 $p_t$ 그리고 PCA등으로 추정된 normal $n_s, n_t$에 대해서 Darboux uvn frame으로 정의한다.

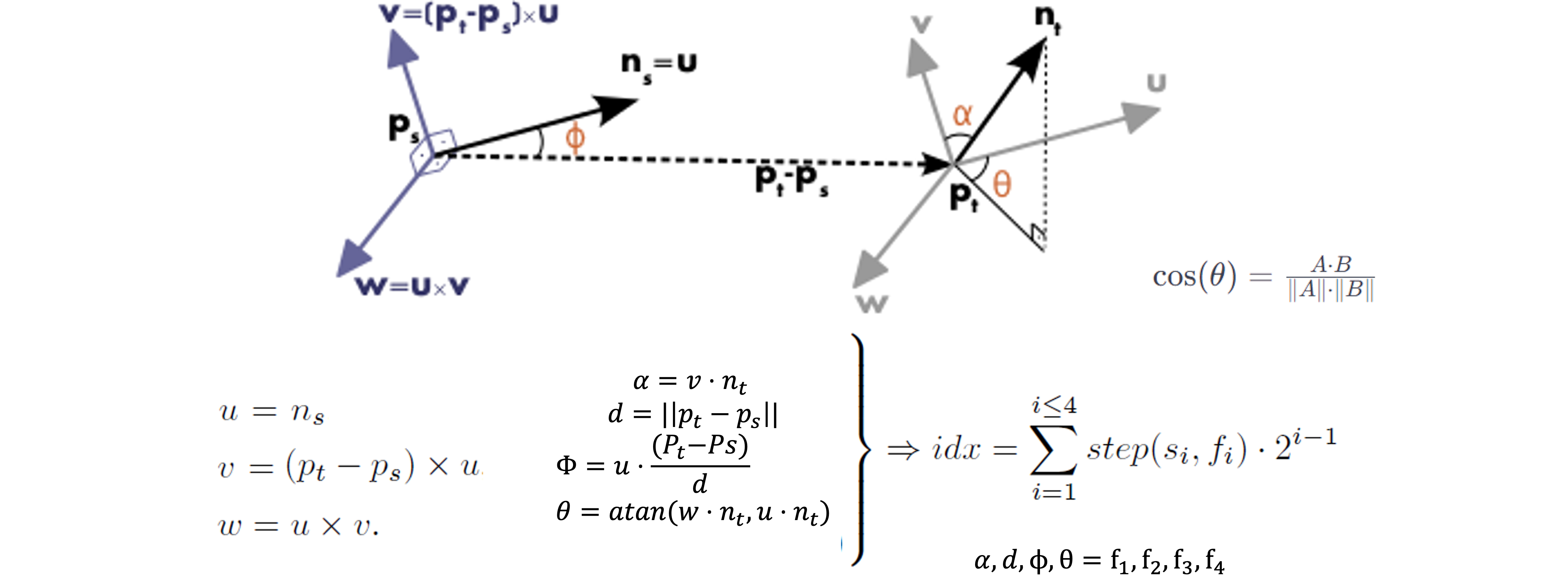
점 $p_s$에 대한 normal 벡터 $n_s$를 $u$로 정의하고, $p_t - p_s$ 벡터와 $u$벡터의 외적을 통해 $v$벡터를 찾는다. 그리고 $u$와 $v$벡터의 외적을 통해 $w$를 찾는다. 이렇게 $u,v,w$를 구하면 이웃점$p_t$와의 관계를 정의할 수 있다. $\alpha, d, \phi, \theta$ 에서 $d$를 제외한 나머지 정보는 각도 정보이다.

$\alpha, d, \Phi, \theta$ 를 $f_1,f_2,f_3,f_4$ 라고 노테이션만 바꾼다. 이 값들을 가지고 $s_i$라는 threshold를 통해 해당 값보다 크면 1 작으면 0을 출력하도록 $step$ 함수를 거친다. idx를 구하는 이유는 몇 번째 히스토그램의 bin에 count될 것인지 결정하기 위해서 이다.

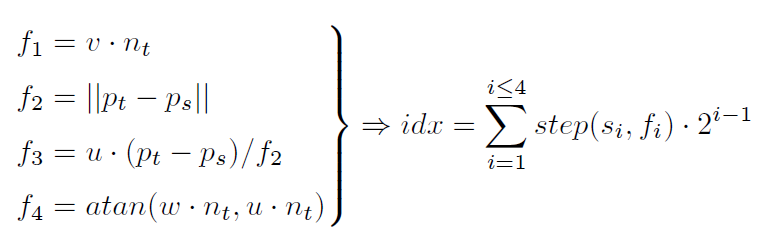
idx 수식을 살펴 보면 i는 우리가 가지고 있는 정보 4가지보다 클 수 없다. 따라서 각 정보마다 $2^{i-1}$ 가중치를 주어 가장 작은 값은 0, 가장 큰 값은 15가 나온다. 이를 히스토그램으로 나타내면 16개의 bin을 가지게 된다. 16개로 제한한 이유는 연산량 때문이다. 모든 점들에 대해서 계산을 하여 집계하면 다음과 같은 히스토그램이 만들어진다.

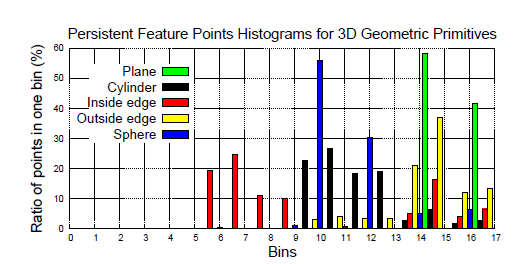
Sphere라는 point cloud(pc)가 지닌 히스토그램, Cylinder라는 pc가 지닌 점들의 특성에 따라 히스토그램의 분포가 달라지는 것을 볼 수 있다. 이렇게 pc의 점들의 특성을 나타낼 수 있다.

Fast Point Feature Histogram(FPFH)

앞선 PFH 방법은 모든 이웃점 쌍에 대해서 연산이 필요하다. 시간 복잡도를 살펴보자.

Time complexity of FPH: $O(nk^2)$ ∵ $c$ (time of computing single pair)$\times\frac{k(k-1)}{2}\times n$ (for all points)

Time complexity of FPFH: $O(nk)$ ∵ $c$ (time of computing single pair)$\times k \times n$ (for all points)

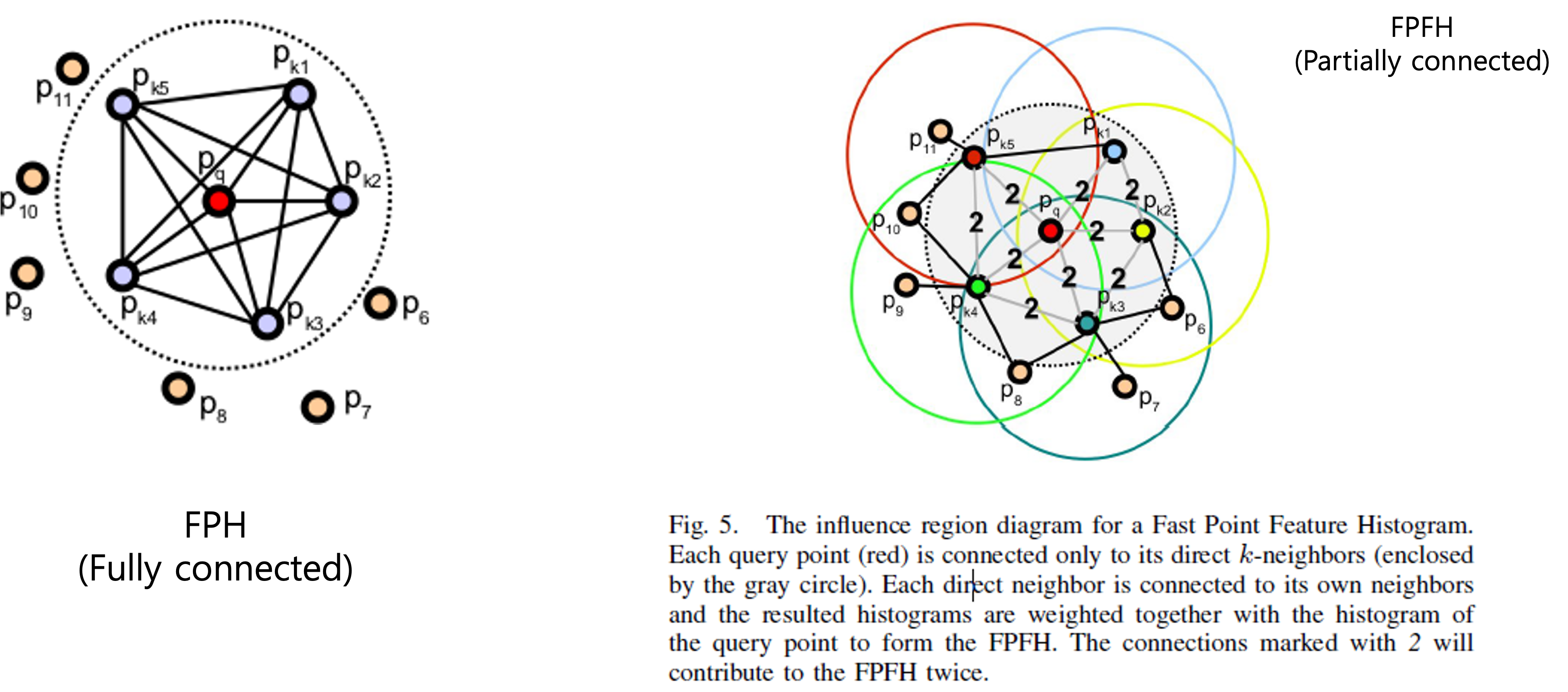
오른쪽의 FPFH는 이웃 점들끼리의 관계는 파악하지 않고 선택한 임의의 기준점과 이웃들간의 관계만 파악한다. 대신 그림에서 2라는 숫자는 기준점과 이웃점간의 관계를 파악한 후 각 이웃점들이 기준점이 되어 이웃점들간의 관계를 한번 더 파악하기 때문에 기존의 기준점과의 관계는 2번 연산하게 되어 2로 표시되어 있다.

정리하면 그림의 예시처럼 임의의 첫 번째 기준점에 대해서 이웃 5개의 점과 관계를 파악하고 이웃점 5개에 대해서 다시 knn을 하여 점들간의 관계를 파악하여 집계한다. 아래의 그림을 보자.

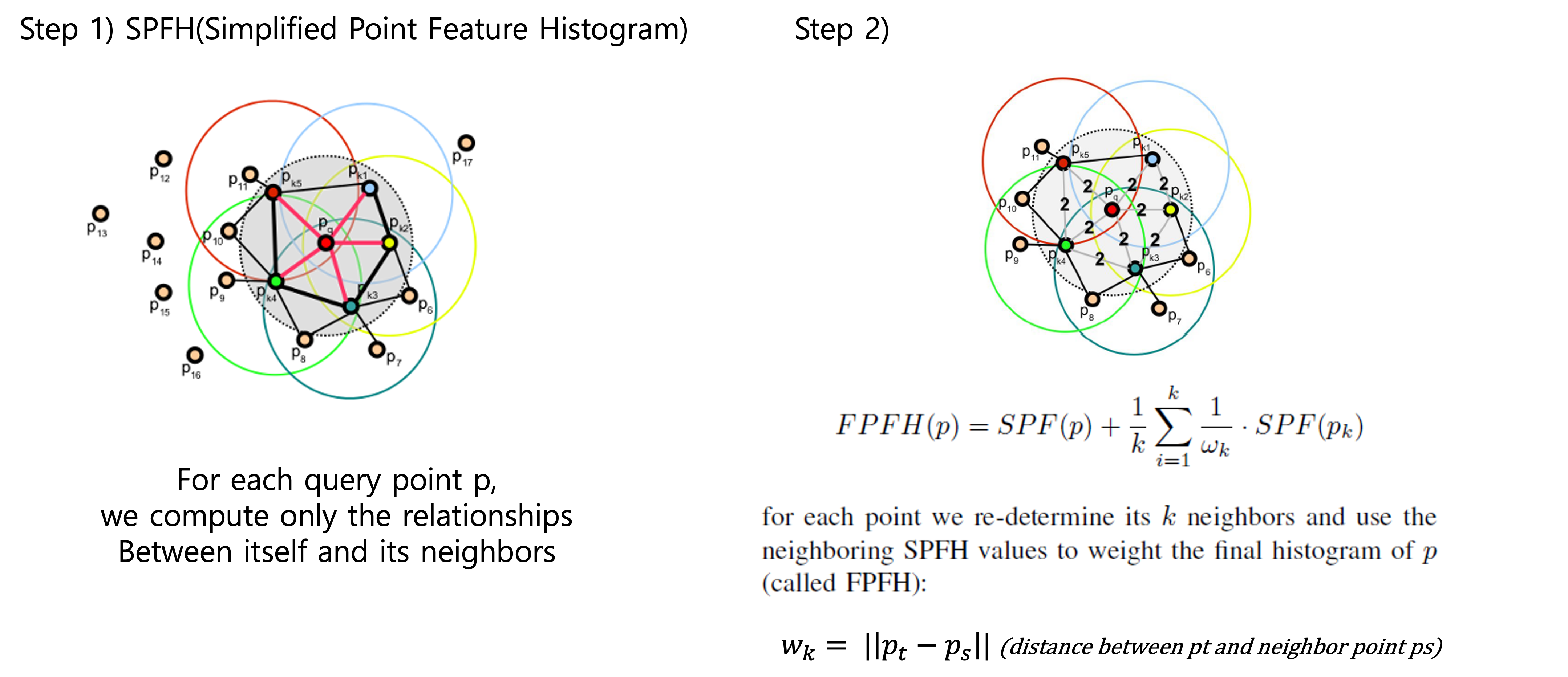
여기서 SPF노테이션은 SPFH와 같은 의미로 Simplified Point Feature (Histogram)이다.

PFH는 4개의 관계를 파악하였는데 FPFH에서는 $d$를 구하지 않고 3개의 관계를 파악한다. 이유는 점들간의 불변한 형태를 파악하기 위해 거리 정보를 제거한다.

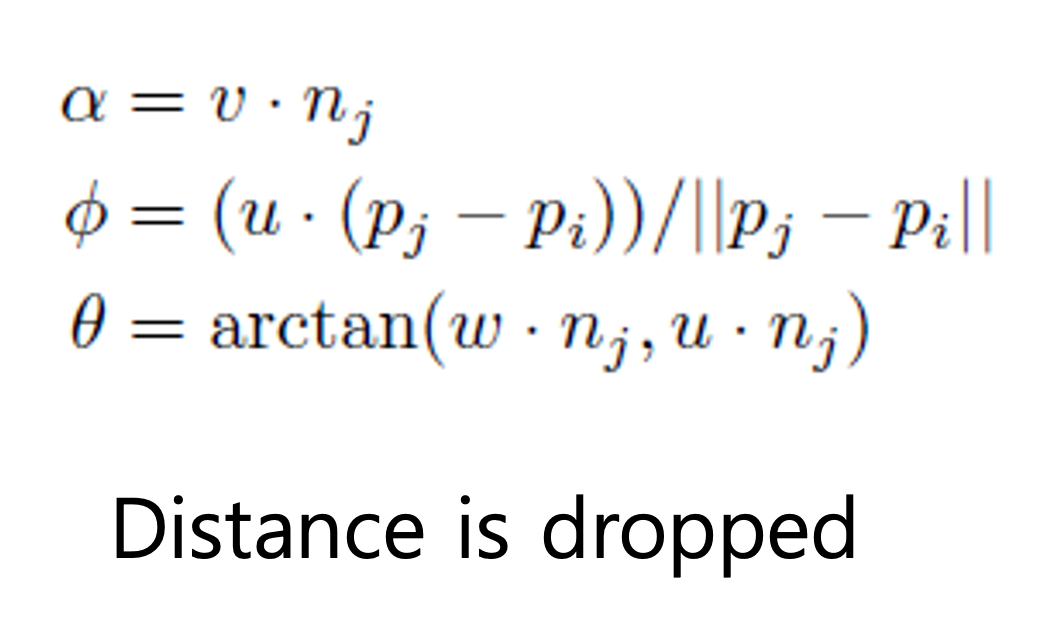
PFH와 FPFH의 차이

FPFH는 PFH의 계산 속도와 효율성을 향상시킨 버전이다. 두 기술 모두 3차원 포인트 클라우드 데이터에서 주변 포인트들의 특징을 히스토그램으로 표현한다. 그런데 FPFH는 계산 속도를 높이기 위해 다음과 같은 변화를 도입했다.

1. 이웃 포인트 연결: FPFH는 PFH와 달리 모든 이웃 포인트를 연결하지 않기 때문에, 쿼리 포인트 주위의 일부 기하학적 정보가 누락될 수 있다.

2. 표면 모델링: PFH는 쿼리 포인트 주변의 정확한 표면을 모델링하는데, 이는 ( r ) 반경의 구에 한정된다. FPFH는 ( r ) 반경뿐만 아니라 최대 ( 2r )까지의 포인트도 고려하여 더 많은 정보를 포함한다.

3. 재가중치: FPFH는 재가중치 스킴을 사용하여 SPFH 값들을 결합하고 일부 정보를 되찾는다.

4. 복잡성: FPFH의 복잡성은 PFH보다 훨씬 낮아져, 실시간 어플리케이션에서의 사용이 가능해졌다.

5. 결과 히스토그램: FPFH는 ( d ) 개의 별도 특징 히스토그램을 만들어 값을 분리(decoupling)하고, 이를 결합하여 하나의 히스토그램을 생성한다. 이는 각 특징 차원의 상관관계를 줄이고 데이터의 차원을 감소시킨다.