Latent Diffusion Models (LDM) 설명: 효율적인 이미지 생성의 혁신

들어가며: 기존 Diffusion Model의 한계

기존의 Diffusion Model은 뛰어난 이미지 생성 성능을 보여주었지만, 하나의 치명적인 문제가 있었습니다. 바로 고해상도 픽셀 공간에서 직접 연산을 수행하기 때문에 엄청난 계산 비용이 든다는 점이었죠. 1024x1024 해상도의 이미지 하나를 생성하기 위해서는 수백만 개의 픽셀에서 수천 번의 노이즈 제거 연산을 수행해야 했습니다.

Latent Diffusion Model의 혁신적 아이디어

Latent Diffusion Model(LDM)은 이 문제를 우아하게 해결했습니다. 핵심 아이디어는 "왜 굳이 픽셀 공간에서 모든 작업을 해야 할까?"라는 단순한 질문에서 출발했습니다.

1. 3단계 파이프라인

LDM은 다음과 같은 3단계 파이프라인으로 작동합니다:

📥 1단계: 압축 (Perceptual Compression)

• 인코더(E)를 통해 고해상도 원본 이미지를 잠재 공간(Latent Space)으로 압축
• 사람 눈에 잘 보이지 않는 고주파수 디테일은 버리고, 중요한 의미적 정보만 보존
• 이미지 크기는 대폭 줄어들지만 핵심 정보는 그대로 유지

🎯 2단계: 잠재 공간에서의 확산 (Latent Diffusion)

• 압축된 잠재 공간에서 기존 diffusion 과정 수행
• 훨씬 작은 차원에서 연산하므로 계산 효율성 대폭 향상
• U-Net 구조를 사용하여 노이즈 예측 및 제거

📤 3단계: 복원 (Decoding)

• 디코더(D)를 통해 잠재 표현을 다시 고해상도 이미지로 복원
• 최종적으로 고품질의 이미지 생성 완료

2. 수학적 표현의 변화

기존 Diffusion Model의 손실 함수:

LDM의 손실 함수:

차이점을 보시면, $x_t$ (픽셀 공간의 노이즈 이미지) 대신 $z_t$ (잠재 공간의 노이즈 표현)를 사용합니다. 이 작은 변화가 엄청난 효율성 향상을 가져다줍니다.

제공하신 수식을 다시 한번 설명해 드릴게요.

$L_{LDM} := \mathbb{E}_{E(x),\epsilon\sim N(0,1),t} [||\epsilon - \epsilon_\theta(z_t; t)||^2_2]$

이 수식은 Latent Diffusion Models(LDM)의 학습 목표를 나타냅니다. 간단히 말해, 모델이 예측한 노이즈와 실제 노이즈 간의 차이를 최소화하도록 학습시키는 것입니다.

수식의 각 부호 및 변수 설명

• $L_{LDM}$: Latent Diffusion Model의 손실 함수(Loss Function)를 의미합니다. 모델 학습을 위해 최소화해야 하는 값입니다.
• $\mathbb{E}$: 기댓값(Expectation)을 의미합니다. 훈련 데이터 전체에 대한 평균 손실을 계산합니다.
  • $E(x)$: 인코더($E$)를 통해 얻은 원본 데이터 $x$의 잠재 표현입니다.
  • $\epsilon \sim N(0,1)$: 표준 정규분포($N(0,1)$)에서 샘플링된 노이즈를 의미합니다. 모델이 맞춰야 할 '정답' 노이즈입니다.
  • $t$: 노이즈가 추가된 시간 단계를 의미합니다. 1부터 $T$까지의 정수 값 중 무작위로 샘플링됩니다.
• $||\cdot||_2^2$: L2-노름(Euclidean norm)의 제곱입니다. 두 벡터의 각 원소별 차이를 제곱하여 더한 값으로, 실제 노이즈와 예측된 노이즈 간의 차이를 측정합니다.
• $\epsilon$: 위에서 설명한, 실제로 추가된 노이즈입니다. 모델이 예측해야 하는 '정답'입니다.
• $\epsilon_\theta(z_t; t)$: $\theta$로 매개변수화된 모델을 의미합니다. 이 모델은 입력으로 노이즈가 추가된 잠재 표현 $z_t$와 시간 단계 $t$를 받아서, $z_t$에 있는 노이즈를 예측합니다.
  • $z_t$: 잠재 표현에 노이즈를 추가하여 만들어진, $t$ 단계의 노이즈가 포함된 잠재 표현입니다. 이는 $E(x)$에 $\epsilon$를 $t$ 단계만큼 추가하여 계산됩니다.
  • $t$: 모델에 노이즈 단계를 알려주어, 각 단계에 맞는 노이즈를 예측하도록 돕는 조건 정보입니다.

LDM 아키텍처 분석

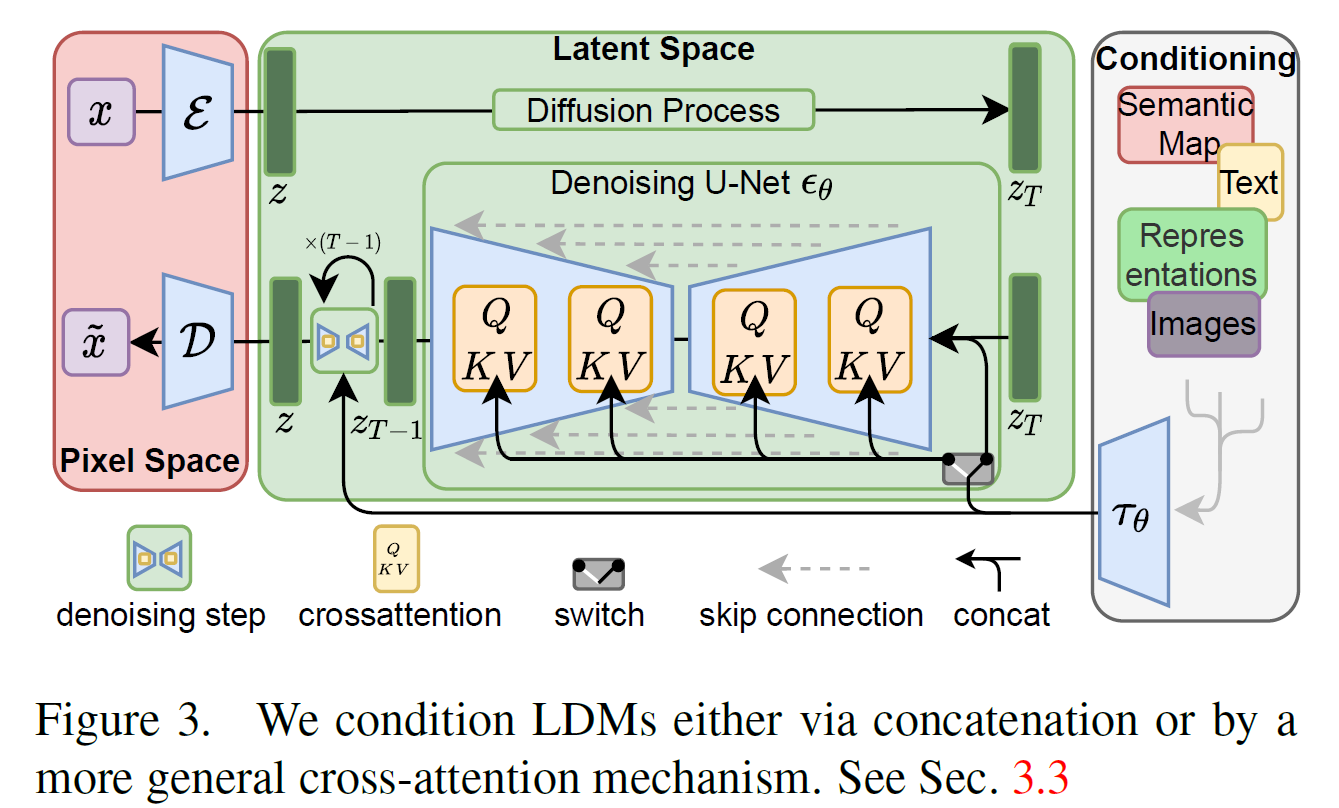
🖼️ Pixel Space (왼쪽)

• $x$: 원본 입력 이미지
• $\mathcal{E}$: 인코더 (주로 CNN 기반 구조, MLP 아님!)
• $\mathcal{D}$: 디코더 (역컨볼루션/전치 컨볼루션 기반)
• $x̃$: 최종 생성된 이미지

🧠 Latent Space (중앙)

• $z$: 인코더가 생성한 깨끗한 잠재 표현
• $z_T$: 최대 노이즈가 추가된 잠재 표현 (여기서 T는 최대 노이즈 단계)
• $ε_θ$: 핵심 노이즈 제거 네트워크 (Denoising U-Net)

🎛️ Conditioning (오른쪽)

LDM의 가장 강력한 특징 중 하나는 조건부 생성입니다:

• 다양한 조건 입력: 텍스트, 의미 맵, 다른 이미지 등
• $τ_θ$: 조건을 모델이 이해할 수 있는 형태로 변환
• Cross-attention: Q, K, V 메커니즘을 통해 조건 정보를 U-Net에 주입

시간 단계 t의 의미

그림에서 보이는 t는 단순한 시간이 아닙니다:

• t=1: 원본에 가까운, 노이즈가 적은 상태
• t=T: 완전히 노이즈로 뒤덮인 상태
• 모델은 $z_T → z_{T-1} → ... → z_1 → z$ 순서로 점진적 노이즈 제거

추론 시간 최적화

"왜 T번 모두 디코딩해야 하나요?"라는 질문이 나올 수 있습니다. 정답은 "꼭 그럴 필요는 없다"입니다!

⚡ 가속화된 샘플링 기법들:

• DDIM: 50~100 스텝만으로 고품질 생성
• Classifier-free Guidance: 품질과 속도 동시 향상
• 최신 기법들: 10~20 스텝만으로도 충분한 결과

LDM의 실제 응용

🎨 Stable Diffusion

• LDM 구조를 기반으로 한 대표적인 오픈소스 모델
• 텍스트-투-이미지 생성의 새로운 표준

🖌️ 다양한 조건부 생성

• 텍스트 프롬프트
• 스케치-투-이미지
• 이미지 인페인팅
• 스타일 전환

왜 LDM이 게임체인저인가?

✅ 장점들:

1. 계산 효율성: 픽셀 공간 대비 10-100배 빠른 연산
2. 메모리 효율성: 훨씬 적은 VRAM 사용
3. 확장성: 다양한 조건부 생성 가능
4. 품질: 기존 방법 대비 동등하거나 더 나은 결과

🔧 기술적 디테일:

• U-Net: 2D 컨볼루션 + 크로스 어텐션의 하이브리드
• 인코더/디코더: CNN 기반 (MLP 아님)
• 잠재 공간: 의미적 정보 보존, 불필요한 디테일 제거

마무리: AI 이미지 생성의 새로운 패러다임

Latent Diffusion Model은 단순히 계산을 빠르게 만든 것이 아닙니다. "무엇이 정말 중요한 정보인가?"라는 근본적 질문에 답하며, AI가 이미지를 이해하고 생성하는 방식을 완전히 바꿔놓았습니다.

현재 우리가 사용하는 대부분의 AI 이미지 생성 도구들이 LDM 기반이라는 사실만 봐도, 이 기술의 혁신성을 알 수 있습니다. 앞으로도 이 기술을 기반으로 한 더욱 놀라운 발전들을 기대해볼 수 있을 것입니다.

---