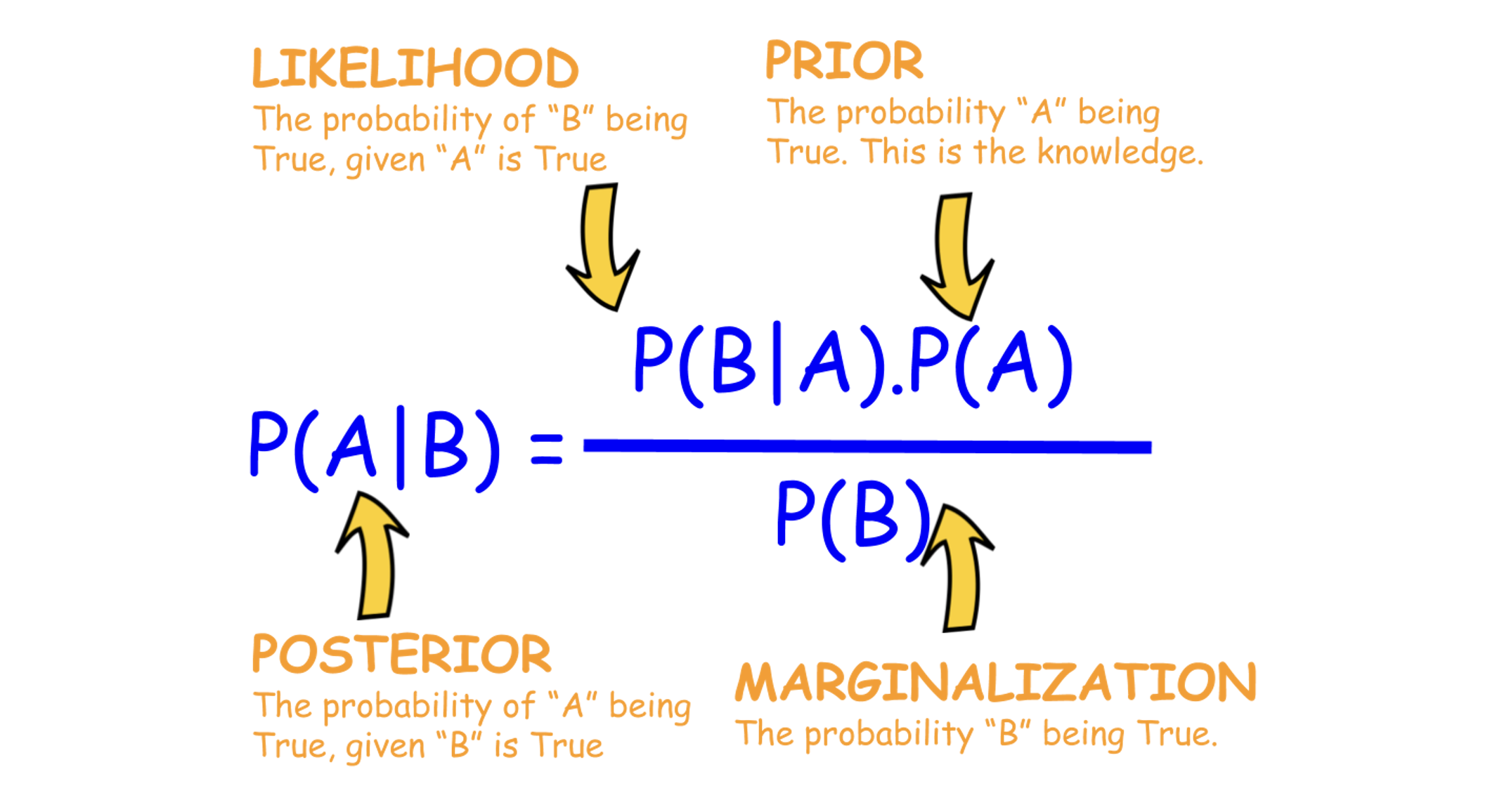
베이즈 정리
어떠한 사후 확률을 구하는 것을 말한다.. 이는 어떤 사건이 만들어 놓은 상황에서, 그 사건이 일어난 후 앞으로 일어나게 될 다른 사건의 가능성을 구하는 것.
정리만 보면 어려우니 간단히 예를들어 설명하자.
동전을 던지면 1/2 확률로 앞면이 나온다.
- 동전의 앞뒷면이 명확히 정해져 있기 때문에 이를 통해 확률을 정의하였고 이는 참이 맞다.
그렇다면 동전을 던졌을때 앞면이 나왔다고 해서 확률이 1/2로 나온것인가?
- 여기서 우리는 간단히 맞다고 생각할 것이지만 조금 억지를 보태서 동전의 앞뒤면이 똑같이 생겼을 수도있다. 때문에 1/2이라고 확신하는것에는 무리가 있는 것이다.
즉, 베이지안 정리는 어떠한 데이터의 분포를 통해 사후 확률을 유추하는것이 된다. 예를들어 내가 응원하는 야구팀이 오늘 이길 확률은 얼마나 될까? 라는 문제 정도가 될 수 있겠다.
사후 확률 추정
데이터를 이용한 베이즈 정리는 현재와 이전 경험을 토대로 특정 데이터 값을 모아 어떤 사건의 확률을 추론하는 알고리즘으로 이해할 수 있다.
예를 한번 들어 보자
어떤 사람이 병 A에 걸렸을 확률을 계산해 보아라
1. 전 세계 인구 중 해당 질병에 걸릴 확률은 1%이다.
2. 정확도가 90%인 검사를 받았더니 양성 판정을 받았다.
3. 이 사람이 실제 병에 걸려있을 확률은 얼마인가?
- 여기서의 문제의 해결은 양성판정을 받았을때 실제 병에 걸려있을 확률이다.
즉 을 구하는게 목표가 된다. - 정확도가 90%인 검사라는 것은 해당 사람이 병에 걸렸다는 전제 하에 양성일 확률이 90%라는 의미이다 때문에 이다.
- 전 세계 인구 중 해당 질병에 걸릴 확률은 1%이니 은 0.01이다.
그렇다 면 공식을 통해 유도해보자.
위 식에서 값은 이라는 데서 유도해낸 것이다.
여기서 양성판정 정확도가 90%임에도 유병확률이 8.3%인 이유는 전체 인구 중 병을 앓고 있는 사람이 1%밖에 되지 않기 때문이다. 때문에 병이 없음에도 있다고 오진한 경우가 병이 실제로 있는 경우보다 더 많은 이유다.
귀납적 추론..
베이즈 정리는 경험에 기반한 선험적인, 혹은 불확실성을 내포하는 수치를 기반으로 이에 추가 정보를 바탕으로 계속된 사전확률을 계산하는데에 있다. 위 예제를 통해서 전 세계 인구 중 병이 있을 확률이라고 정의한 1%가 사실은 수많은 데이터를 통해 얻은 사전 확률이라고 생각 한다면 더 많은 데이터가 모임에 있어서 그 확률이 개선 될 수 있고 우리는 그에 따라 새로운 사후 확률을 계산할 수 있는 것이다. 이와 같은 방법은 귀납적 추론 방법으로써 연역적 사고를 기반으로 하는 기존 확률에 새로운 패러다임을 가져왔다고 볼 수 있다.
