Bias와 Variance
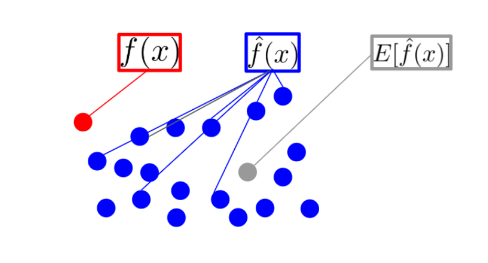
- f(x) : 입력 데이터 x에 대하여 실제 정답에 해당하는 값 => 그림에서의 빨간 점
- f^(x) : 머신러닝 모델에 입력 데이터 x를 넣었을 때, 모델이 출력하는 예측 값
이 값은 모델의 상태(파라미터 값)에 따라 다양한 값들을 출력할 수 있음 => 그림에서의 파란 점 - E[f^(x)] : f^(x)의 평균(기대값)으로 대표 예측값
=> 그림에서의 회색 점
1. Bias
- 모델을 통해 얻은 예측값과 실제값과의 차이의 평균
- 예측값이 실제 정답값과 얼마나 떨어져 있는지를 나타냄
- Bias가 높다고 하면 예측값과 실제값의 차이가 크다는 것
<예측값과 실제값과의 차이의 평균)
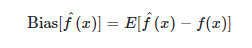
2. Variance
- 데이터 셋에 대해 예측값이 얼마나 변화할 수 있는지에 대한 양(Quantity)의 개념
- 모델이 얼마나 flexibilty를 가지는 지에 대한 의미로, 예측값이 얼마나 퍼져서 다양하게 출력될 수 있는지 해석 가능
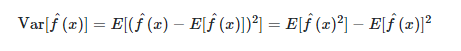
3. 머신러닝 모델에서의 bias와 variance의 관계
- bias와 variance는 머신러닝 모델의 학습 상태를 나타낼 수 있는 좋은 척도임
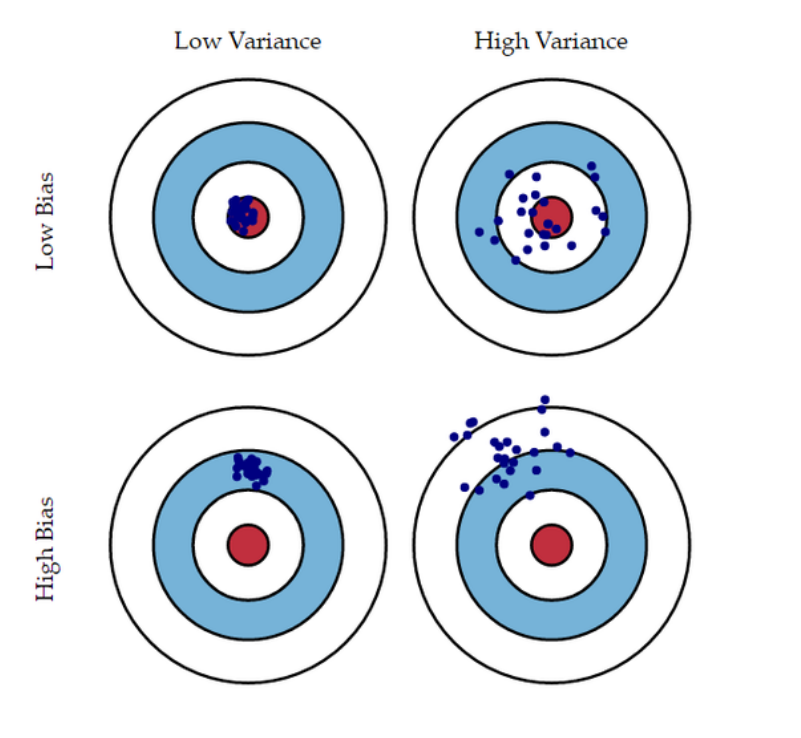
위의 그림처럼 4가지 케이스로 분류 할 수 있다.
(1) 낮은 bias, 낮은 variance
- 예측값이 실제값 근방에 분포하고 예측값들이 서로 몰려있음
(2) 낮은 bias, 높은 variance
- 예측값이 정답 근방에 분포하지만, 예측값들이 서로 흝어져 있음
(3) 높은 bias, 낮은 variance
- 예측값이 정답 근방에 분포하지 않지만, 예측값들이 서로 몰려있음
(4) 높은 bias, 높은 variance
- 예측값이 정답 근방에 분포하지 않고, 예측값들도 흝어져 있음
- 가장 적합한 구간은 (1)의 낮은 bias와 낮은 variance
3-(1) regression 측면에서의 bias와 variance
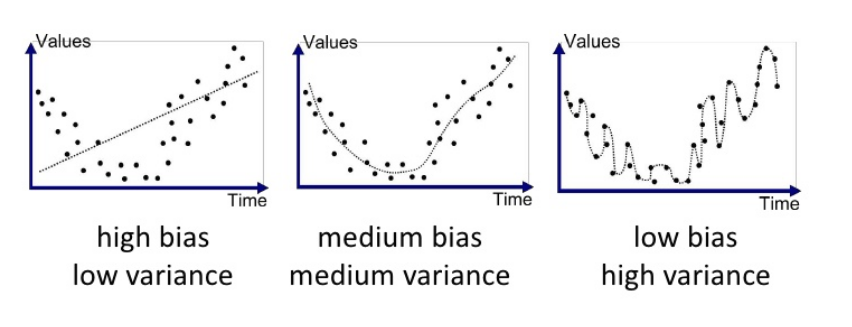
- 위 그림에서 점선은 예측값, 점은 time에 해당하는 실제값이다.
(1) 첫번째 그래프는 high bias & low varinace
높은 bias와 낮은 variance로 볼 수 있는데, 예측값인 점선이 실제 점과 많이 다르지만 점선의 편차가 작기 때문이다.
(2) 두 번째 그래프는 medium bias & medium variance로, 보통의 bias와 보통의 variance 이다.
첫번째 그래프에 비해 점선인 예측값이 점인 실제값과 상대적으로 유사하고, 점선인 예측값들의 편차가 상대적으로 크다.
(3) 세 번째 그래프는 low bias & high variance로,
낮은 bias와 높은 variance 이다. 점선인 예측값이 점인 실제 선과 굉장히 유사해 낮은 bias를 보이지만 모델의 예측값인 점선이 구불구불해져서 예측값들의 편차가 크다.
3-(2) classification 측면에서의 bias와 variance
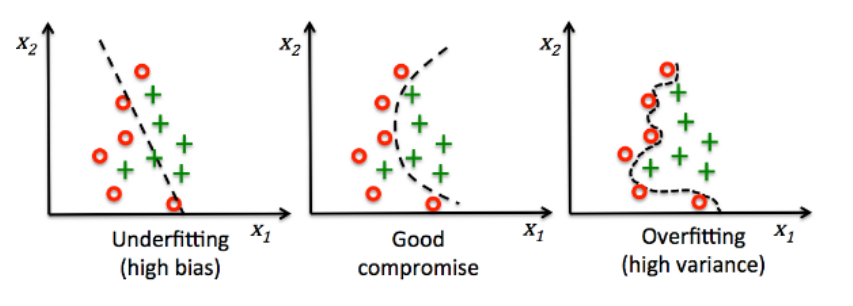
(1) 첫번째 그래프에서 높은 bias와 낮은 variance를 보이는데, high bias(높은 bias)는 모델의 성능이 정답을 잘 예측하지 못하는 경우로 underfitting 이 발생한 경우이다.
(2) 세번째 그래프는 낮은 bias와 high variance를 보이는데, 모델이 필요 이상으로 복잡해서 예측값 간의 편차가 크게 발생한 경우로 overfitting이 발생했다고 볼 수 있다.
- 이와 같이 bias와 variance는 모델 복잡도와 관련이 있으며 둘은 서로 영향을 끼치고 있다.
- bias를 낮추기 위해서 모델 복잡도를 높이게 되면 variance가 증가해서 overfitting이 발생하고, variance를 줄이기 위해서 모델의 복잡도를 낮추게 되면 bias가 증가해서 underfitting이 발생함
- 따라서, 적당한 수준의 bias와 variance를 만들기 위해 적정한 수준에서 모델의 학습을 종료시켜야 함
4. 모델 복잡도
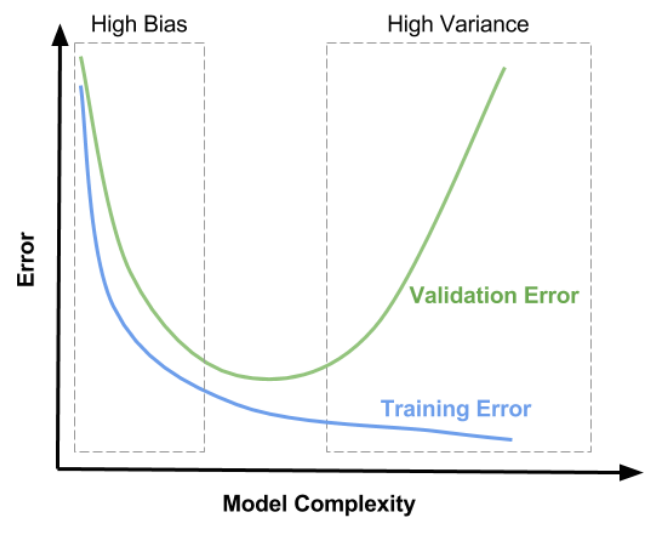
- 위 그림과 같이 train, validation 데이터 셋을 이용하는 방법이 있는데, train 데이터를 통해 학습을 하면서 trian error를 줄여나가면 bias는 점점 줄어들고 variance는 점점 증가하게 된다.
- 이 때 validation 데이터도 동시에 error를 계산하여 validation error도 감소하다가, 다시 증가하는 지점을 확인해 low(medium) bias & low(medium) varaince를 찾는다.
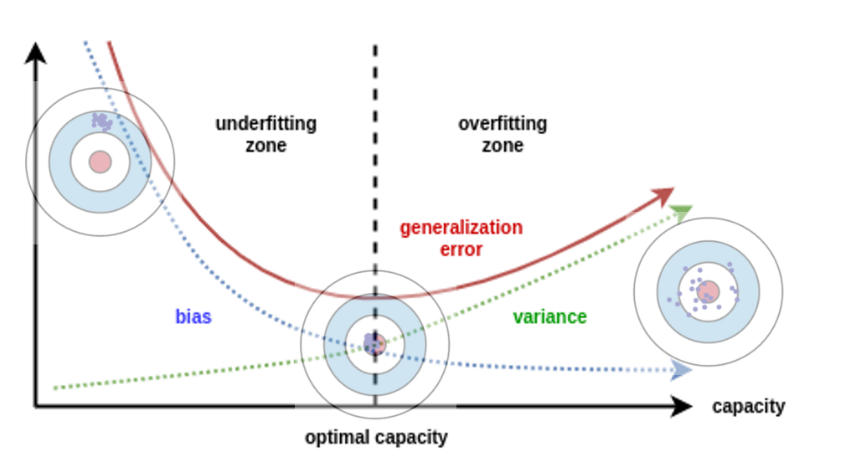
- 위 그래프로 보면 전형적인 학습 진행 현황을 확인할 수 있는데, underfitting과 overfitting 구간을 나누어 볼 수 있다.
- 학습을 진행할수록 generalization error에 대한 곡선이 줄어들다가 다시 증가하는 지점이 발생하는데, 이 지점에서 low(medium) bias, low(medium) variance를 만족한다.
5. Bias VS Variance
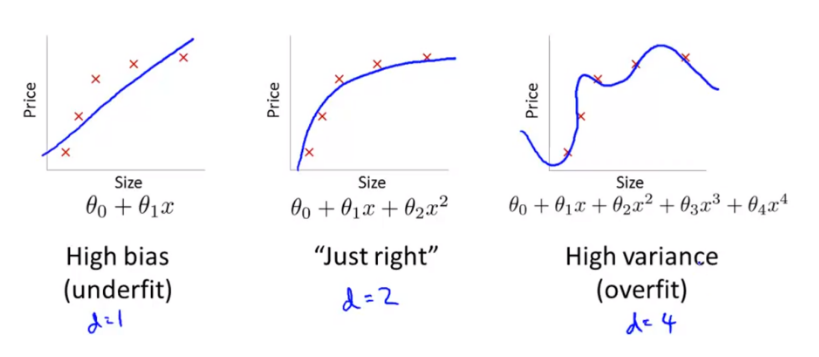
- Bias와 Varianc 문제의 정의를 살펴보면, bias 문제는 데이터의 분포에 비해 모델이 너무 간단한 경우 underfit이 발생한다.
- variance 문제는 모델의 복잡도가 데이터 분포보다 커서 데이터를 overfit 한다.
정리
- 머신러닝에서 Bias는 예측값과 실제값의 차이이고, Variance는 예측값끼리의 차이이다.
- 머신러닝에서의 Bias와 Variance는 trade-off 관계인데, Bias와 Variance를 더해 에러를 측정한다.
- Bias가 높으면 모델이 학습이 제대로 되지 않은 과소적합 상태이고, Variance가 높으면 모델이 과하게 학습된 과적합 상태이다.
- 기타 데이터셋과 학습률, 파라미터 변화에 따른 bias와 variance는 시간을 좀 들여서 정리해야 할 것 같으므로 여기서 stop.
human-level performance 하다가 여기까지 와버림
