< 분류에서 사용하는 성능지표 >
ref) https://yngie-c.github.io/machine%20learning/2020/05/01/val_eval/
1. Confusion Matrix
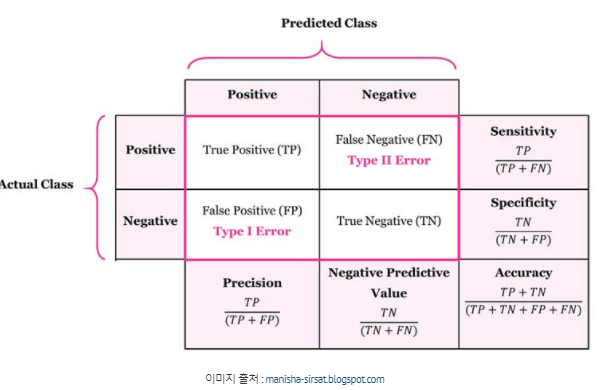
분류에서 가장 많이 사용되는 오분류표이다. 행렬의 배치는 그리는 사람에 따라 달라질 수 있으며, Scikit learn에 기반한 confusion matrix는 다음과 같다.
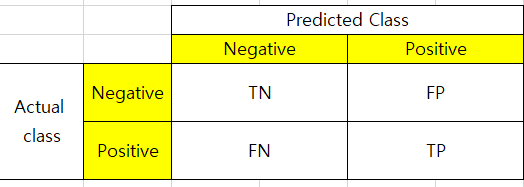
FP: 예측은 참이나 실제는 거짓, 제 1종 오류
FN: 실제는 참이나 예측은 거짓, 제 2종 오류
정밀도에서는 FP를 줄이는 것, 재현율에서는 FN을 줄이는 것이 중요하다.
즉 FP, FN이 커지면 정밀도, 재현율 각각 작아진다.
-
정확도(Accuracy)
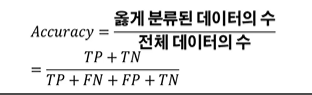
: 전체 데이터 중에서 예측한 값이 실제 값과 부합하는 비율 -
정밀도, 재현율, 특이도

정밀도(precision): 예측이 참인 값 중 실제 참인 값
재현율(recall,Sensitivity,TPR): 실제 참인 값 중 예측도 참인 값
특이도(specificity): 예측이 거짓인 값 중 실제 거짓인 값
2. Precision-Recall Trade-off
로지스틱 회귀 모형에서 특정 이메일이 스팸일 확률이 0.9이면 스팸일 가능성이 매우 높다고 예측할 수 있다. 이와 반대로 0.03이라면 스팸이 아닐 가능성이 높다. 그렇다면 0.6인 이메일의 경우 어떻게 분류해야 할까?
이때 분류할 기준이 필요한데, 이 기준을 임계값(Threshold)이라 한다.
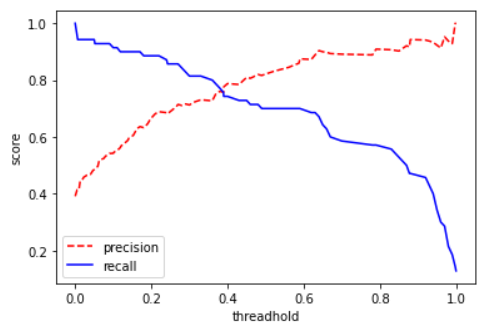
어떤 분류기의 임계값에 따른 정밀도와 재현율을 그래프로 나타내면 위과 같으며, Precision과 Recall이 만나는 점이 최적의 임계값이다.
임계값을 높이면(Positive로 판별하는 기준을 빡빡하게 잡으면) 정밀도는 올라가고 재현율은 낮아진다.
반대로 임계값을 낮추면(기준을 널널하게 잡으면) 정밀도는 낮아지고 재현율은 높아진다.
이를 정밀도-재현율 트레이드 오프(Precision-Recall Trade-off)라 한다.
*어떤 것을 분류하느냐에 따라 정밀도가 더 중요할 때가 있고, 재현율이 더 중요할 때도 있다. 스팸 메일 분류기는 FP를 줄이는 즉 정밀도, 암 환자 분류기는 FN을 줄이는 즉 재현율을 각각 더 중요하게 생각해야 한다.
3. G-mean, F1 measure
- G-mean, F1 measure

실제 데이터의 특성상 정확도보다는 제1종 오류와 제2종 오류 중 성능이 나쁜 쪽에 더 가중치를 주는 G-mean지표나 정밀도와 재현율만 고려하는 F1 measure가 더 고려해볼 수 있는 지표이다. 둘 다 높으면 높을 수록 좋은 지표이다. (F1 measure가 더 자주 쓰인다.)
4. ROC curve, AUC
- ROC curve
: 양성에 대한 오답/정답 비율 시각화
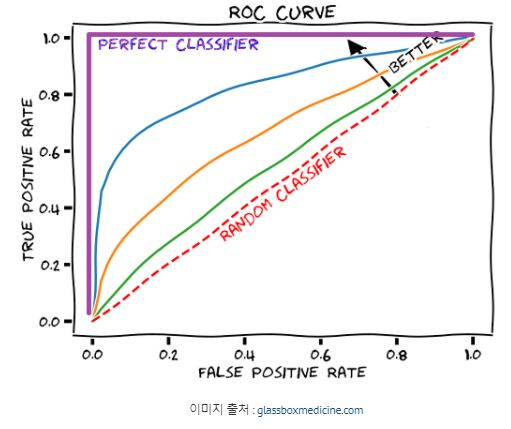
가로축을 1-특이도(FPR), 세로축을 재현율(TPR)로 하여 시각화한 그래프이다.
FPR과 TPR은 오차 행렬 내 4개의 요소를 사용한 수치이며 다음과 같다.
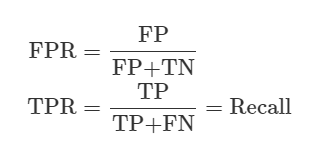
FPR: 실제 Negative 클래스인 인스턴스를 얼마나 잘못 분류했는지를 나타내는 수치.
TPR: 실제 Positive인 클래스인 인스턴스를 얼마나 제대로 분류했는 지를 나타내는 수치.
임계값(Threshold)을 변화시키면 FPR이 변하게 된다.
임계값이 높으면(1) 정밀도(Precision)가 높아지며 FP가 낮아지므로(FN이 높아지므로) FPR은 0이다.
반대로, 임계값이 낮으면(0) FP가 높아지고(FN 낮아지므로)TN은 0이므로 FPR은 1이다. 즉 임계값이 낮추면 더 많은 항목이 양성으로 분류되므로 FPR과 TPR이 모두 증가한다.
이렇게 임계값에 따라 FPR을 0~1까지 변화시켜가며 그에 따라 TPR이 어떻게 변화하는지 기록한 것이 ROC curve이다.
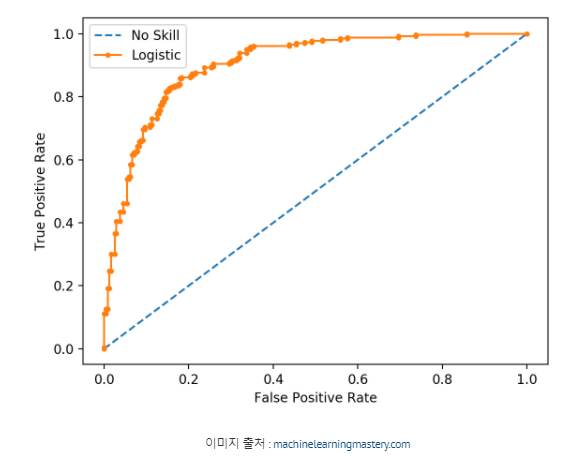
-AUC(area under the curve): ROC곡선 아랫부분 면적
: 0~1사이의 값을 가지며, AUC값은 클수록 좋다.
from sklearn.metrics import classification_report, confusion_matrix,accuracy_score, precision_score,recall_score,f1_score
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import roc_auc_score,roc_curve
#오분류표
confusion_matrix(y_test,y_vld)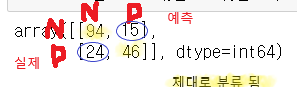
24는 FN으로 실제는 참이나, 예측은 거짓이다. 즉 생존자를 사망자로 잘못 예측한 경우이다. 반대로 15는 FP이며 사망자를 생존자로 잘못 예측했다. 이 때문에 정확도가 떨어진다.
# 간략하게 한 번에 보고 싶을 때 사용
classification_report(y_test,y_vld)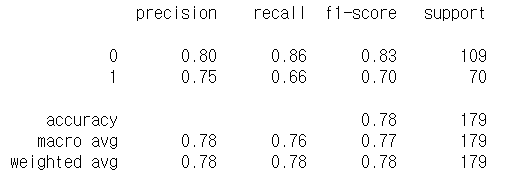
# 위에(cr)보다 아래 코드를 더 자주 사용한다.
accuracy_score(y_test,y_vld)
precision_score(y_test,y_vld)
recall_score(y_test,y_vld)
f1_score(y_test,y_vld)
# 예측 확률
proba= model.predict_proba(X_test)
# precision,recall은 trade off관계, precision_recall_curve( )
precision,recall,th = precision_recall_curve(y_test,proba[:,1])
plt.xlabel('threadhold') #임계값
plt.ylabel('score')
plt.plot(th,precision[:len(th)],'red',linestyle = '--',label = 'precision')
plt.plot(th,recall[:len(th)],'blue',label = 'recall')
plt.legend()
plt.show()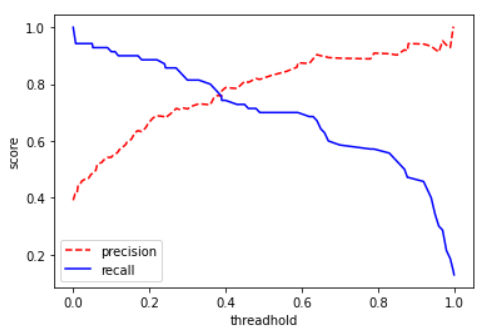
# roc_curve( )
fpr,tpr,th = roc_curve(y_test,proba[:,1])
plt.xlabel('FPR-False Positive')
plt.ylabel('TPR-True Positive ')
plt.plot(fpr,tpr,'red',label = 'rate')
plt.plot([0,1],[0,1],'blue',linestyle = '--',label = 'th 0.5')
plt.legend()
plt.show()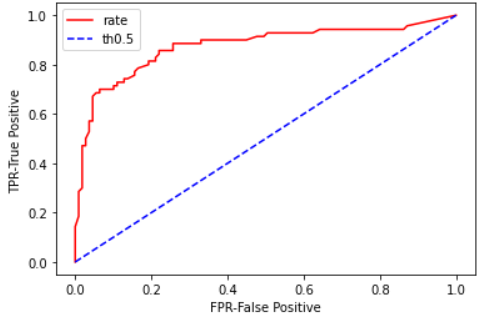
임계값 조정
임계값(Threshold)을 조정해 정밀도 또는 재현율의 수치를 높일 수 있다. 하지만 정밀도와 재현율은 trade off관계이기 때문에 한쪽이 올라가면 다른 한쪽이 떨어지기 쉽다.
일반적으로 임계값을 0.5로 정하고 이보다 크면 positive, 작으면 negative이다. predict_proba()를 통해 레이블별 예측확률을 반환한다.
- Binarizer
: threshold 기준값보다 같거나 작으면 0을, 크면 1을 반환한다.
<임계값을 0.5로 설정한 경우>
from sklearn.preprocessing import Binarizer
# Binarizer의 threshold 값을 0.5로 설정
custom_threshold = 0.5
#즉 Positive 클래스의 컬럼 하나만 추출하여 Binarizer를 적용
proba_1 = proba[:,1].reshape(-1,1)
binarizer=Binarizer(threshold=custom_threshold).fit(proba_1)
custom_pred = binarizer.transform(proba_1)
recall=recall_score(y_test, custom_pred)
acc=accuracy_score(y_test, custom_pred)
print(f"재현율:{recall}, 정확도:{acc:.4f}")
<임계값을 0.4로 설정한 경우>
from sklearn.preprocessing import Binarizer
# Binarizer의 threshold 값을 0.4로 설정
custom_threshold = 0.4
# predict_proba() 결과 값의 두 번째 컬럼,
#즉 Positive 클래스의 컬럼 하나만 추출하여 Binarizer를 적용
proba_1 = proba[:,1].reshape(-1,1)
binarizer=Binarizer(threshold=custom_threshold).fit(proba_1)
custom_pred = binarizer.transform(proba_1)
recall=recall_score(y_test, custom_pred)
acc=accuracy_score(y_test, custom_pred)
print(f"재현율:{recall:.4f}, 정확도:{acc:.4f}")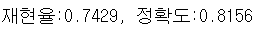
임계값을 낮추면 recall이 상승하고, precision이 떨어진다.
