[머신러닝] 다중선형회귀분석

단순선형회귀분석과 같은 데이터셋을 사용한다.

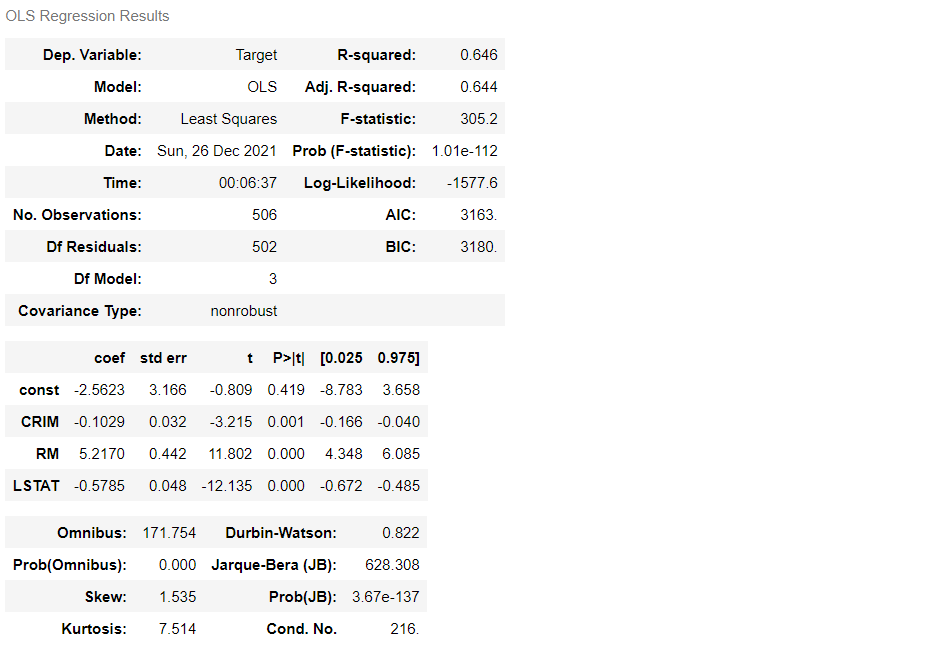
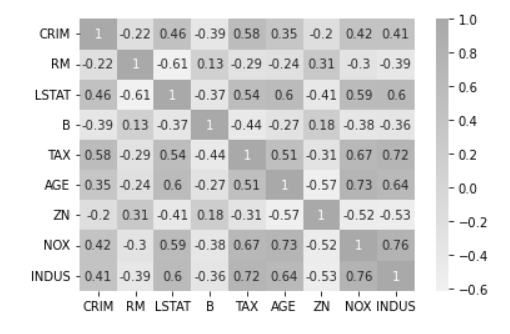
상관계수/산점도를 통해 다중공선성 확인

# bostan data에서 원하는 변수만 추출
x_data2=boston[['CRIM','RM','LSTAT',"B","TAX","AGE","ZN","NOX","INDUS"]] 

# 상관행렬 
x_data2.corr()

## 상관행렬 시각화 
import seaborn as sns;
cmap = sns.light_palette("darkgray", as_cmap=True)
sns.heatmap(x_data2.corr(), annot=True, cmap=cmap)
plt.show()

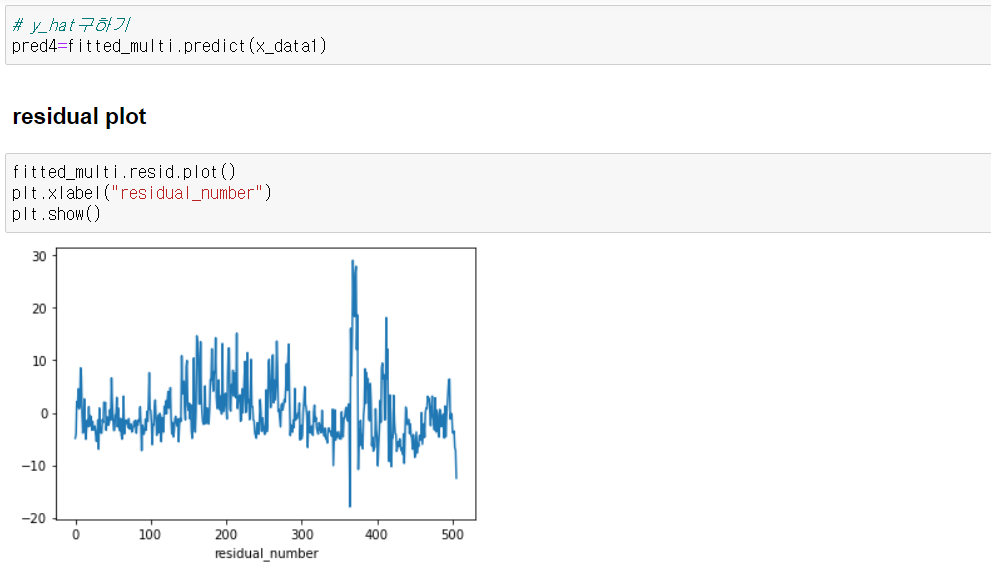
## 변수별 산점도 시각화
sns.pairplot(x_data2)
plt.show()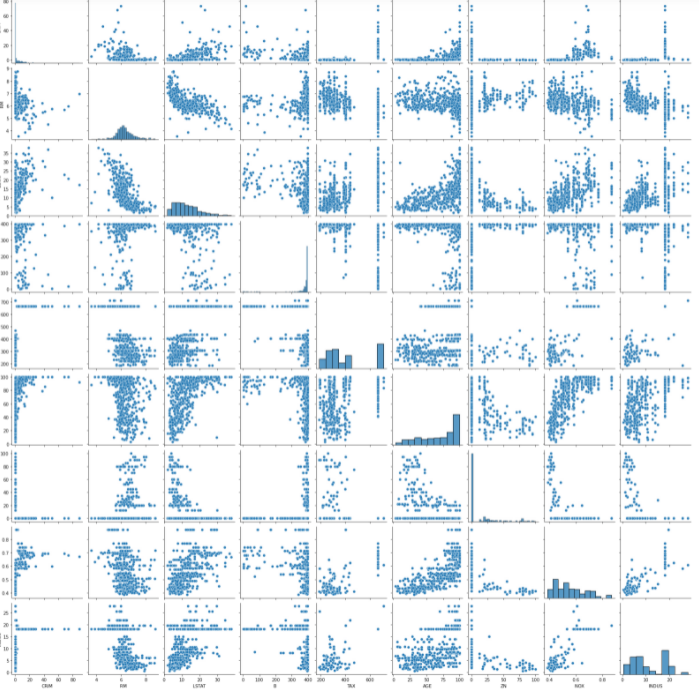

VIF를 통한 다중공선성 확인

from statsmodels.stats.outliers_influence import variance_inflation_factor

vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(
    x_data2.values, i) for i in range(x_data2.shape[1])]
vif["features"] = x_data2.columns
vif

VIF가 10 이상이면 다중공선성이 있다고 판단하고, 10이상인 변수들을 하나씩 제거해보면서 VIF를 확인한다.

## nox 변수 제거후(X_data3) VIF 확인 
vif = pd.DataFrame()
x_data3= x_data2.drop('NOX',axis=1)
vif["VIF Factor"] = [variance_inflation_factor(
    x_data3.values, i) for i in range(x_data3.shape[1])]
vif["features"] = x_data3.columns
vif

## RM 변수 제거후(x_data4) VIF 확인 
vif = pd.DataFrame()
x_data4= x_data3.drop('RM',axis=1)
vif["VIF Factor"] = [variance_inflation_factor(
    x_data4.values, i) for i in range(x_data4.shape[1])]
vif["features"] = x_data4.columns
vif

# nox 변수 제거한 데이터(x_data3) 상수항 추가 후 회귀 모델 적합
# nox, rm 변수 제거한 데이터(x_data4) 상수항 추가 후 회귀 모델 적합
x_data3_=sm.add_constant(x_data3,has_constant="add")
x_data4_=sm.add_constant(x_data4,has_constant="add")

model_vif=sm.OLS(target,x_data3_)
fitted_model_vif=model_vif.fit()
model_vif2=sm.OLS(target,x_data4_)
fitted_model_vif2=model_vif2.fit()

## 회귀모델 결과 비교 
fitted_model_vif.summary()
fitted_model_vif2.summary()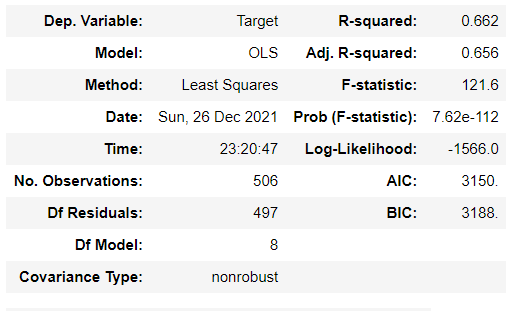

RM변수를 제거했더니 R square값이 낮아졌다. 중요한 변수로 제거하면 안되는 변수이다.

학습/검증데이터 분할

from sklearn.model_selection import train_test_split
X = x_data2_
y = target
train_x, test_x, train_y, test_y = train_test_split(X, y, train_size=0.7, test_size=0.3,random_state = 1)
print(train_x.shape, test_x.shape, train_y.shape, test_y.shape)

# train_x에 회귀모델 적합
fit_1=sm.OLS(train_y,train_x)
fit_1=fit_1.fit()

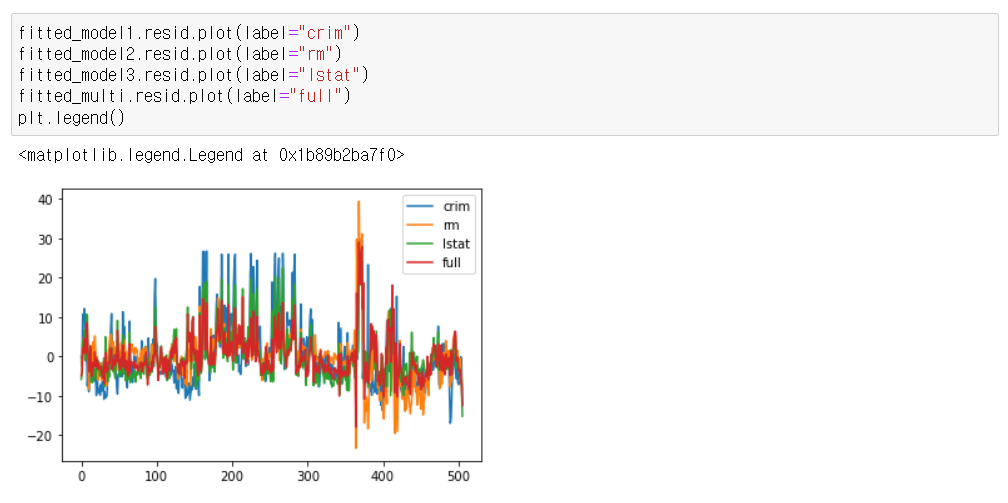
## 검증데이터에 대한 예측값과 true값 비교 
plt.plot(np.array(fit_1.predict(test_x)),label="pred")
plt.plot(np.array(test_y),label="true")
plt.legend()
plt.show()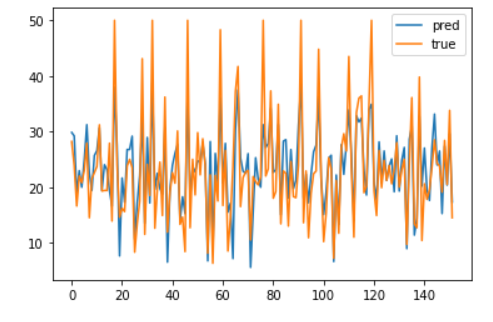

# x_data3 학습 검증데이터 분할
X = x_data3_
y = target
train_x2, test_x2, train_y2, test_y2 = train_test_split
(X, y, train_size=0.7, test_size=0.3,random_state = 1)

#x_data4 학습 검증데이터 분할
X = x_data4_
y = target
train_x3, test_x3, train_y3, test_y3 = train_test_split
(X, y, train_size=0.7, test_size=0.3,random_state = 1)

# x_data3/x_data4 회귀 모델 적합(fit2,fit3)
fit_2=sm.OLS(train_y2,train_x2)
fit_2=fit_2.fit()
fit_3=sm.OLS(train_y3,train_x3)
fit_3=fit_3.fit()

## true값과 예측값 비교 
plt.plot(np.array(fit_2.predict(test_x2)),label="pred")
plt.plot(np.array(fit_3.predict(test_x3)),label="pred")
plt.plot(np.array(test_y2),label="true")
plt.legend()
plt.show()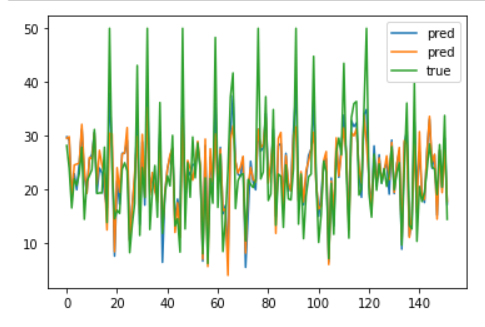

## full모델 추가해서 비교 
plt.plot(np.array(fit_1.predict(test_x)),label="pred")
plt.plot(np.array(fit_2.predict(test_x2)),label="pred_vif")
plt.plot(np.array(fit_2.predict(test_x2)),label="pred_vif2")
plt.plot(np.array(test_y2),label="true")
plt.legend()
plt.show()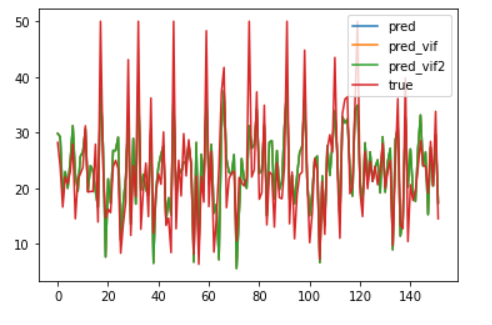

#잔차 
plt.plot(np.array(test_y2['Target']-fit_1.predict(test_x)),label="pred_full")
plt.plot(np.array(test_y2['Target']-fit_2.predict(test_x2)),label="pred_vif")
plt.plot(np.array(test_y2['Target']-fit_3.predict(test_x3)),label="pred_vif2")
plt.legend()
plt.show()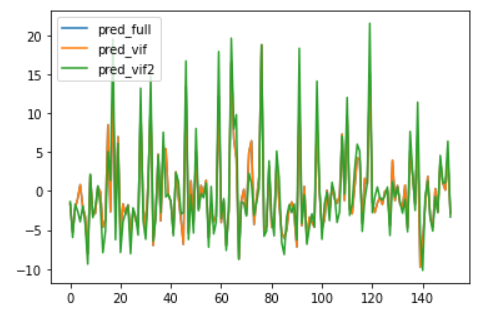

MSE를 통한 검증데이터에 대한 성능비교

from sklearn.metrics import mean_squared_error

mean_squared_error(y_true=test_y['Target'],y_pred=fit_1.predict(test_x))

mean_squared_error(y_true=test_y['Target'],y_pred=fit_2.predict(test_x2))

mean_squared_error(y_true=test_y['Target'],y_pred=fit_3.predict(test_x3))

MSE는 각각 26.148, 26.140, 38.78이며 fit_1,fit_2모델의 성능이 좋다고 판단된다.
(MSE값은 작을 수록 좋음)