PART 04.
1. 변수선택법
-모델 선택(변수 선택)
: 변수가 여러 개일 때 최선의 변수 조합을 찾아내는 기법
변수의 수가 p개일 때 변수의 총 조합은 2^p으로 변수 수가 증가함에 따라 변수 조합의 수는 기하급수적으로 증가
1) Feedforward Selection 방법
:변수를 추가해가며 성능지표를 비교해가는 방법으로 AIC가 작을수록 좋음

2) Backward Elimination 방법
:변수를 제거해가며 성능지표를 비교해가는 방법

3) Stepwise 방법
:가장 유의한 변수를 추가하거나 유의하지 않는 변수를 제거해나가는 방법.
전진선택법의 각 단계에서 이미 선택된 변수들의 중요도를 다시 검사하여 중요하지 않은 변수를 제거하는 방법, 일반적으로 가장 널리 쓰이는 방법

2. 교호작용
:변수 간의 시너지 효과
(x1과 x2는 y에 영향을 끼치지 않지만, x1과 x2가 결합됨으로써 y에 중요한 영향을 끼칠 수 있다)
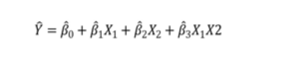
-명목형 변수(Dummy variable)
성별,대학,지역 등 명목형 변수의 경우 전처리 필요.
3. 회귀분석의 진단
-회귀모델을 만든 후 잘 만들어진 모델인지 진단이 필요하다.
잔차에는 정규성,독립성,등분산성 세가지 가정이 존재

-일반적으로 Residuals산점도, Normal Q-Q Plot과 Residual vs fitted plot으로 진단
-잔차가 가정에 위배된 경우
1) Y에 대하여 log 또는 root를 씌워 줌
2) 이상치 제거
3) 다항회귀분석
4. 다항회귀분석
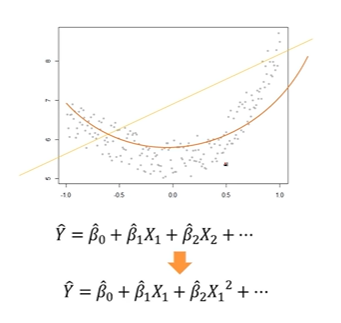
다항회귀분석이 필요한 경우
-독립변수와 종속변수간의 비선형관계를 가질 경우 (plot을 통해 확인 가능)
-다중회귀의 가정에 위배된 경우 (residual plot을 통해 확인 가능)
다항회귀 적합
-회귀계수 추정) 선형회귀분석과 동일하게 잔차제곱합을 최소화시키도록 추정한다.
*항이 추가될수록 과적합이 알어날 가능성이 크기 때문에 고차항을 추가할 시에는 신중해야 한다. (최대 2차항까지 넣는다.)
5. 로지스틱 회귀
로지스틱 회귀는 출력 변수를 직접 예측하는 것이 아니라, 두 개의 카테고리를 가지는 binary형태의 출력 변수 (성공/실패,예/아니오를 예측할 때 사용하는 회귀분석 방법)
ex) 반도체 공정에서 특정 변수 값을 가지고 정상이냐 불량이냐 분류. 이때 y는 정상(0), 불량(1) 2가지 범주를 갖는 출력 변수이며, 입력 변수로는 반도체 공정의 특정변수를 사용하여 예측함.
*불량 확률이 음수가 될 수 없기 때문에 단순선형회귀를 이용하는 것은 적절하지 않음.
-로지스틱 함수(Logistic Function)
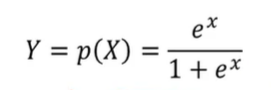
6. 로지스틱 회귀분석 추정
최대우도법(maximum likelihood)를 사용한다.
베르누이 확률분포(0 또는 1의 값을 가지는 확률 변수의 확률 분포)를 이용하여 추정
7. 회귀계수 축소법
회귀계수를 축소하는 이유
1) 잡음(noise)을 제거해 모형의 정확도 개선
2) 모형의 연산 속도 빨라짐
3) 다중공선성의 문제를 완화시켜 모형의 해석 능력을 향상
(많은 모형에서 입력 변수들끼리 독립임을 가정하지만, 입력 변수들끼리 상관관계를 가지는 경우가 대부분)
계수축소법의 종류
1)Ridge 회귀 2) Lasso 회귀 3) Elastic-Net 회귀
회귀계수 축소법에서는 SSE에 회귀계수를 축소하는 항을 추가한다.
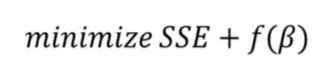
1. Ridge Regression
Ridge 회귀에서는 f(B)에 회귀계수의 제곱의 합을 대입
람다는 크면 클수록 보다 많은 회귀계수를 0으로 수렴

2.Lasso Regression
lasso회귀에서는 f(B)에 회귀계수의 절대값의 합을 대입.
람다는 크면 클수록 보다 많은 회귀계수를 0으로 수렴
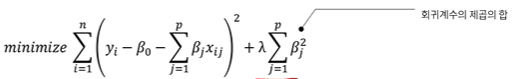
*람다 값을 변화시켜가며 MSE가 최소일 때의 람다를 탐색
<Ridge 회귀와 Lasso의 차이점>
-Ridge는 계수를 축소하되 0에 가까운 수로 축소하는 반면,Lasso는 계수를 완전히 0으로 축소함.
-Ridge회귀: 입력 변수들이 전반적으로 비슷한 수준으로 출력 변수에 영향을 미치는 경우에 사용
-Lasso회귀: 출력 변수에 미치는 입력 변수의 영향력 편차가 큰 경우에 사용
3.Elastic-Net 회귀
Lasso와 Ridge회귀의 정규화 회귀 모델
Lasso에 적용된 회귀계수의 절대값의 합과 Ridge에 적용된 제곱의 합을 모두 f(B)에 대입
다수의 변수 간에 상관관계가 존재할 때 효과적
출처: 패스트캠퍼스 머신러닝&AI첫걸음 시작하기 2주차, 위키백과
